5.2. Torque (or moment of force)

Let the body, in the plane perpendicular to the axis of rotation 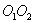there is a force 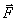(Fig.5.2). We decompose this force into two components: 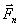and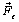

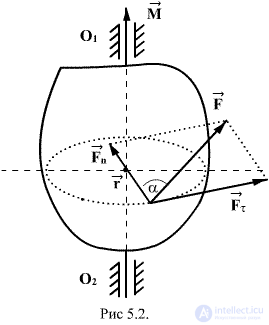
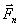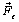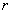Strength intersects the axis of rotation and, therefore, does not affect the rotation of the body. Under the action of the component the body will rotate around the axis . Distance from the axis of rotation to the line along which the force acts 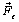called shoulder strength 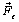. The moment of force relative to point O is the product of the modulus of force. 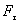on the shoulder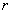

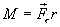
Given that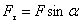

moment of power

.

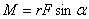From the point of view of vector algebra, this expression represents the vector product of the radius-vector 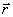held at the point of application of force 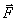on this force. Thus, the moment of force relative to point O is a vector quantity and is equal to

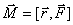(5.1)

The vector of moment of force is directed perpendicular to the plane drawn through the vectors. 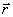and 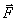, and forms with them the right three of vectors (when observed from the top of the vector M, it can be seen that the rotation is the shortest distance from 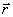to 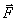going counterclockwise).