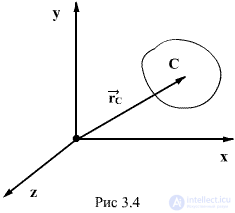
In the above Newton's equation, it was assumed that the body is so small in size that it can be considered a material point. The motion of any non-deformable body of finite size can be described by equations similar to (3.6), if we introduce the concept of "center of mass" ("center of inertia") of the body. If the body consists of n material points with masses 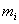 and radius vectors
and radius vectors 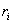 then the center of mass of the system of material points is called such a CC, the radius vector of which is defined as follows:
then the center of mass of the system of material points is called such a CC, the radius vector of which is defined as follows:
 | (3.7) |
Where 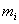 and
and 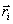 is the mass and radius-vector of the i-th point of the system, m is the total mass of the system.
is the mass and radius-vector of the i-th point of the system, m is the total mass of the system.
Accordingly, the relations between the Cartesian coordinates of the center of inertia and all points of the system have the form:
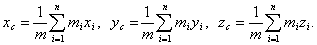
Inertia center speed:
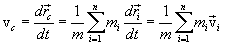 | (3.8) |
Impulse system The geometric sum of the impulses of all material points of the system is called the impulse of the system and is denoted by the letter 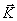 :
:
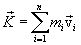 ,
,
then the center of mass velocity
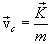 | (3.9) |
Thus, from (3.9) it follows that the impulse of the system is equal to the product of the mass of the entire system and the speed of its center of inertia:
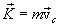 | (3.10) |


Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics