3.12. Guidelines for solving problems in dynamics

In classical physics, as has already been shown, the state of a material point is completely determined by its x, y, z coordinates . and speed components 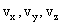at a given time, i.e. particle radius vector 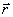and its speed. Given these functional dependencies, Newton's second law is the following:

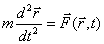(3.14)

If we assume that the resultant force 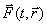as a function of coordinates and time is known, then the equation (3.14) in the mathematical classification is a second-order vector differential equation with respect to the radius vector 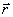material point.

Solving equation (3.14) with a given right side, you can determine the radius-vector of the body at any time and, thereby, to establish the form of the trajectory of the body. Moreover, based on the principle of independence of motion, the complex vector equation (3.14), which determines the curvilinear body motion in the general case, is replaced by an equivalent system of three equations, each of which simultaneously describes a straight-line motion along the corresponding x, y and z axes.

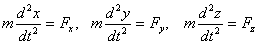(3.15)

Where 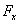, 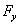and 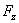- vector projections 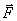on coordinate axes. The coordinates x, y and z are determined by two integrations of equation (3.15). With each integration, an indefinite constant arises. Therefore, for an unambiguous allocation of the law of motion, the equations of motion should be supplemented with two conditions determining these constants. These conditions are fixed by setting the state of a material point at some (usually at the initial) moment of time, i.e. indicating radius vector values 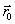or coordinates 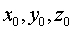and speeds at t = 0. Thus, as a result of integrating equations (3.15), we obtain the coordinates x, y, z as functions of time and two integration constants: