1.5. Material point velocity

To characterize the movement of a material point, a vector physical quantity is introduced - the speed, which determines both the speed of movement and the direction of movement at a given time.

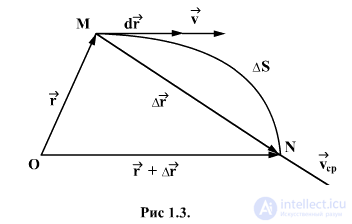
Let the material point move along the curvilinear trajectory MN so that at the moment of time t it is in TM, and at the moment of time 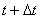in t. N. The radius vectors of points M and N are respectively equal to 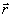and the length of the arc MN is equal to 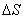(Fig. 1.3).

Medium Speed ​​Vector points in the time interval from t to t + Δ t is called the ratio of the increment the radius vector of a point during this time interval to its value :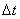

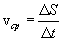(1.5)

The average velocity vector is also directed as a displacement vector. those. along the chord MN.

Instant speed or speed at a given time . If in expression (1.5) go to the limit, directing 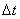to zero, then we get an expression for the velocity vector of the bit. at time t passing it through the TM trajectory.

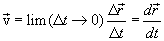(1.6)

In the process of decreasing 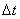the point N approaches t.M., and the chord MN, turning around t.M, in the limit coincides in direction with the tangent to the trajectory at the point M. Therefore, the vector 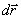and the velocity v of a moving point is directed along a tangential path in the direction of motion. The velocity vector v of a material point can be decomposed into three components directed along the axes of a rectangular Cartesian coordinate system.

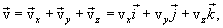(1.7)

Where 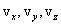- projections of the velocity vector on the x, y, z axes.

Substituting in (1.6) the values ​​for the radius-vector of the material point (1.1) and performing the term by term, we get:

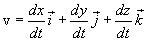(1.8)

From the comparison of expressions (1.7) and (1.8) it follows that the projections of the velocity of the material point on the axis of the rectangular Cartesian coordinate system are equal to the first time derivative of the corresponding coordinates of the point:

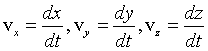(1.9)

Therefore, the numerical value of speed:

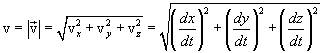(1.10)

Motion in which the direction of the velocity of a material point does not change is called rectilinear. If the numerical value of the instantaneous velocity of a point remains unchanged during movement, then such movement is called uniform.

If, for arbitrary equal intervals of time, a point travels paths of different lengths, then the numerical value of its instantaneous velocity changes over time. Such a movement is called uneven.

In this case, the scalar value is often used. 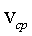called the average ground speed of uneven movement in a given area 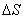trajectories. It is equal to the numerical value of the speed of such a uniform movement, in which the passage 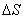spent the same time 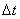, as with a given non-uniform motion:

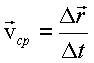(1.11)

Because 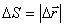only in the case of rectilinear motion with a constant speed in the direction, then in the general case:

.

The law of addition speeds . If a material point simultaneously participates in several movements, then the resulting movement 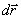in accordance with the law of independence of motion, equal to the vector (geometric) sum of the elementary displacements caused by each of these movements separately:

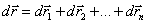
In accordance with definition (1.6):

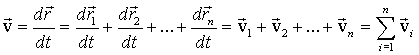(1.12)

So the speed 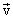the resulting motion is equal to the geometric sum of the speeds 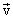all movements in which the material point participates, (this provision is called the law of addition of speeds).