Lecture
Using equations:
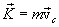 and
and 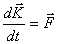 ,
,
we can write
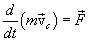
or
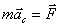 | (3.12) |
Thus, the center of inertia of a mechanical system moves as a material point, the mass of which is equal to the mass of the entire system and on which a force acts, equal to the main vector of external forces applied to the system. In the general case, the motion of a rigid body can be considered as the sum of two motions: translational with velocity 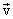 equal to speed
equal to speed 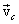 center of inertia of the body, and rotation around the center of inertia. Therefore, the last equation is often called the basic equation of the dynamics of the translational motion of a solid.
center of inertia of the body, and rotation around the center of inertia. Therefore, the last equation is often called the basic equation of the dynamics of the translational motion of a solid.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics