Lecture
With rotational movement, in contrast to translational, speed 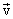 different points of the body are not the same. Therefore, the speed
different points of the body are not the same. Therefore, the speed 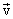 Any point of a rotating body cannot serve as a characteristic of the movement of the whole body.
Any point of a rotating body cannot serve as a characteristic of the movement of the whole body.
Let t. O - the center of rotation of the body, and 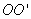 - fixed (or instantaneous) axis of rotation (Fig.2.2).
- fixed (or instantaneous) axis of rotation (Fig.2.2).
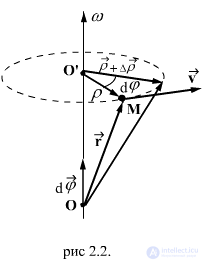
The position of an arbitrary m. Body will be set using the radius vector 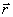 conducted from the center of O. From the figure it is clear that:
conducted from the center of O. From the figure it is clear that:
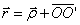 ,
,
Where 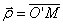 - radius vector drawn to the point of the circular arc along which m moves. For a short time, the vector
- radius vector drawn to the point of the circular arc along which m moves. For a short time, the vector 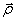 rotates in the plane perpendicular
rotates in the plane perpendicular 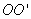 on a small angle
on a small angle 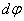 . At the same angle rotates in time.
. At the same angle rotates in time. 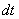 radius vector of any other point of the body, because otherwise the distance between these points should have changed. Thus, the angle of rotation characterizes the movement of the entire rotating body over a small period of time. Convenient to enter a vector
radius vector of any other point of the body, because otherwise the distance between these points should have changed. Thus, the angle of rotation characterizes the movement of the entire rotating body over a small period of time. Convenient to enter a vector 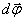 elementary (small) body rotation, numerically equal
elementary (small) body rotation, numerically equal 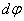 and directed along the instantaneous axis so that from its end the rotation of the body is visible happening counterclockwise.
and directed along the instantaneous axis so that from its end the rotation of the body is visible happening counterclockwise.
Comments
To leave a comment
Physical foundations of mechanics
Terms: Physical foundations of mechanics