6.6. Relativistic impulse

The equations of classical mechanics are invariant with respect to the Galilean transformations, but with respect to the Lorentz transformations they turn out to be non-invariant. From the theory of relativity, it follows that the equation of dynamics, invariant with respect to the Lorentz transformations, has the form:

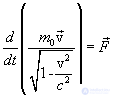
Where 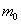- invariant, i.e. the same value in all reference systems called the particle's rest mass, v- particle velocity, 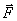- force acting on the particle. Compare to the classical equation.

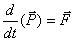
We conclude that the particle’s relativistic impulse is

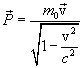(6.7)

Relativistic mass.

Determining the particle mass m as the coefficient of proportionality between speed and momentum, we obtain that the particle mass depends on its speed.

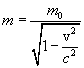(6.8)

Energy in relativistic dynamics.

For particle energy in the theory of relativity, the expression is obtained:

(6.9)

From (2.3) it follows that a particle at rest possesses energy

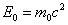(6.10)

This value is called the particle rest energy. Kinetic energy is obviously equal

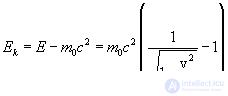(6.11)

Considering that 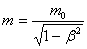, the expression for the total energy of a particle can be written as

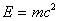(6.12)

From the last expression it follows that the energy and mass of the body are always proportional to each other. Any change in body energy 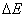accompanied by a change in body weight

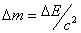
and, conversely, any change in mass 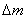accompanied by a change in energy 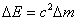. This statement is called the law of the relationship or the law of proportionality of mass and energy.