Lecture
The oscillatory link is an elementary dynamic link of the second order, it has three variable parameters. Therefore, we will pay more attention to its characteristics. Moreover, the oscillating element describes quite complex elements of electromechanical systems and electric drives, for example, such a common element as a DC motor.
The transfer function of the oscillating element -
| (one) |
Where 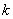 - gain,
- gain, 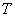 - time constant
- time constant 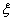 - attenuation coefficient.
- attenuation coefficient.
A distinctive feature of the oscillatory link is that it changes not only its properties, but also its name depending on the magnitude of the attenuation coefficient:
if a 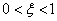 - the link is called oscillatory, since its temporal characteristics are oscillatory in nature;
- the link is called oscillatory, since its temporal characteristics are oscillatory in nature;
if a 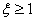 - the link is called the inertial (aperiodic) link of the second order, since its temporal characteristics are monotonous, that is, there are no oscillations;
- the link is called the inertial (aperiodic) link of the second order, since its temporal characteristics are monotonous, that is, there are no oscillations;
if a 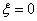 - the link is called conservative, since its temporal characteristics have the form of continuous oscillations, they say, the link preserves vibrations.
- the link is called conservative, since its temporal characteristics have the form of continuous oscillations, they say, the link preserves vibrations.
We obtain the temporal characteristics of the oscillatory level. To do this, we transform its transfer function (1), introducing the notation -
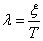 - attenuation rate,
- attenuation rate,
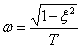 - the angular frequency of oscillation
- the angular frequency of oscillation
| (2) |
From the Laplace transform tables, we have -
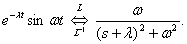
Now we can determine the impulse response of the oscillatory link -
| (3) |
An example of the impulse response is shown in Fig. one.

Fig. one
Define the transient response of the oscillating element -
| (four) |
An exemplary view of the transient response is shown in Fig. 2

Fig. 2
According to fig. 1 and 2, it is easy to judge how the parameters of the oscillatory element affect the temporal characteristics.
We will analyze in more detail the temporal characteristics of the oscillatory level for the case 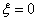 , that is, we define the temporal characteristics of a conservative link.
, that is, we define the temporal characteristics of a conservative link.
The transfer function of the conservative link has the form -
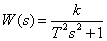 ,
,
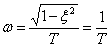 - the angular frequency of oscillation
- the angular frequency of oscillation
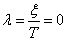 - attenuation rate.
- attenuation rate.
then the expressions of temporal characteristics (3) and (4) take the following form -
| (five) |
| (6) |
The approximate type of characteristics of a conservative link is shown in fig. 3 and 4.

Fig. 3

Fig. four
Determine the frequency response of the oscillatory level.
| (6) |
VCHH -
| (7) |
MCH -
| (eight) |
Frequency response -
| (9) |
Phase response -
| (ten) |
Let's build the VCHH and MCH on the same graph, an approximate view of the characteristics is shown in fig. five.

Fig. five
The approximate type of APCF is shown in fig. 6

Fig. 6
Approximate view of the frequency response and phase response is shown in Fig. 7 and 8, the frequency response function has an extremum ( 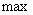 ) at
) at
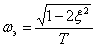 .
.

Fig. 7

Fig. eight
Consider the frequency characteristics of a conservative link ( 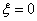 ).
).
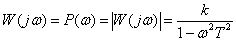 .
.
With 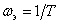 characteristics (see fig. 9) have a gap
characteristics (see fig. 9) have a gap
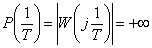 .
.
Fig. 9
Determine the phase response of the conservative link -
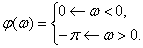
An exemplary view of the phase response is shown in Fig. ten.

Fig. ten
We define the logarithmic characteristics of the oscillatory link.
| (eleven) |
We define the asymptotic LAFC of the oscillatory link
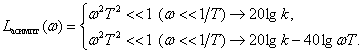
Slope asymptotes -
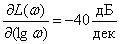 .
.
The maximum deviation of the asymptotic LAFC from the exact -
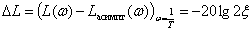 .
.
The approximate type of LAFC and LPCHH is shown in fig. eleven.

Fig. eleven
To obtain the temporal characteristics of the inertial link of the second order ( 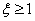 ) suitable and expressions (3) and (4), obtained above for the oscillatory link. But they can be obtained otherwise.
) suitable and expressions (3) and (4), obtained above for the oscillatory link. But they can be obtained otherwise.
If a 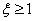 , you can convert link transfer function -
, you can convert link transfer function -
| (12) |
Where
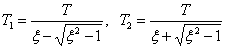 .
.
A link with a transfer function in the form of (12) can be represented in the idea of two aperiodic links, connected in series, as shown in Fig. 12.
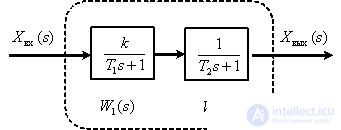
Fig. 12
The impulse characteristics of these links are of the form -
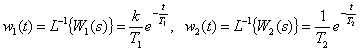 .
.
Then the impulse characteristic of the inertial link of the second order can be obtained using the Laplace transform multiplication of images -
| (13) |
We obtain the transition characteristic by integrating (13) -
| (14) |
The approximate type of temporal characteristics of the inertial (aperiodic) link of the second order is shown in fig. 13.

Fig. 13
We obtain the asymptotic LAFC for the second-order inertial link, representing it in the form of two successively connected aperiodic links, (see Fig. 12).

In fig. 14 and 15 show LAFC of a second-order inertial unit.

Fig. 14

Fig. 15
Test questions and tasks
How does the name of an oscillatory link change and depending on what?
Link Transfer Function -
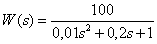 .
.
Determine the frequency of oscillation of the temporal characteristics of this link.
Answer :
Oscillation frequency  .
.
Link Transfer Function -
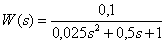 .
.
Determine the attenuation rate of the time characteristics of this link.
Answer :
Attenuation rate 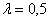 .
.
Link Transfer Function -
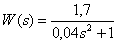 .
.
Determine the frequency of oscillation of the temporal characteristics of this link.
Answer :
Oscillation frequency 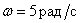 .
.
How many quadrants does the AFC of the oscillatory link go through?
Answer :
Two quadrants.
At what frequency does the frequency response have a conservative link, if its transfer function has the form -
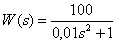 .
.
Answer :
Frequency response frequency response 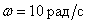 .
.
At what angle does the harmonic signal shift with frequency 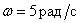 dynamic link with transfer function -
dynamic link with transfer function -
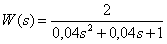 ,
,
and what is the value of the frequency response at this frequency?
Answer :
The phase angle is 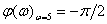 the value of the frequency response -
the value of the frequency response - 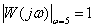 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control