Lecture
Consider the definition of a multidimensional system used in control theory.
Multidimensional systems are called control systems in which there are several, more than one, controlled variables.
A one-dimensional system is characterized by the fact that only one variable of the control object is controlled (measured, regulated). Consider the structure of a typical one-dimensional control system on the example of controlling the speed of rotation of an electric motor.

Fig. one
In the system shown in fig. 1 control object (OA) is an electric motor (D). The motor is affected by an energy converter (PE), which sets the motor in motion and changes the speed by means of the voltage ( 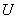 ) supplied to the engine. The engine is also affected by the workload, which creates a moment on the motor shaft (
) supplied to the engine. The engine is also affected by the workload, which creates a moment on the motor shaft ( 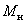 ), leading to a change in speed (
), leading to a change in speed ( 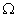 ) unlike the set speed (
) unlike the set speed ( 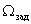 ). In the process of engine operation, when the load changes, the speed will also change, which is unacceptable from the point of view of requirements to the quality of the output, for example, the feed rate of the metal-cutting machine. In the function of speed deviation from the reference, the regulator (P) acts on the energy converter in such a way as to reduce the speed deviation.
). In the process of engine operation, when the load changes, the speed will also change, which is unacceptable from the point of view of requirements to the quality of the output, for example, the feed rate of the metal-cutting machine. In the function of speed deviation from the reference, the regulator (P) acts on the energy converter in such a way as to reduce the speed deviation.
In this case, both the control system as a whole and the control object are represented in the form of a mathematical model having a scalar input, output and disturbing effect.
For analysis and synthesis in such systems, mathematical models are used in the form of differential equations, transfer functions, structural diagram, frequency and time characteristics, which were considered in our course earlier.
The general trend in the development of industrial devices is to improve quality and reduce costs. When improving the quality of management, it is necessary to take into account a greater number of disturbing factors and it is required to manage several object variables. This should ensure the requirements for accuracy, dynamism, stability and efficiency of the process of moving the motor shaft. Then both the control object (engine) and the control system are considered as multidimensional.
The structure of the engine speed control system takes the form shown in Fig. 2

Fig. 2
As we see here as the controlled variables of the engine, not only speed, but also the angle of rotation of the shaft 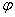 that is often required with an exact shaft stop. Also control the motor load current consumption
that is often required with an exact shaft stop. Also control the motor load current consumption 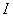 , profitability by efficiency
, profitability by efficiency 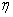 , engine heating according to engine temperature
, engine heating according to engine temperature 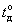 . The system is affected by a disturbance that also has several components: load moment, ambient temperature
. The system is affected by a disturbance that also has several components: load moment, ambient temperature 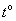 that is important for installations operating in the open air, and the deviation of the parameters of the energy source supplying the energy converter, which is important for autonomous installations. In this case, the control effect on the engine is also a vector quantity.
that is important for installations operating in the open air, and the deviation of the parameters of the energy source supplying the energy converter, which is important for autonomous installations. In this case, the control effect on the engine is also a vector quantity. 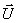 . And this is the case not only in electric drive systems, but in general, when developing automation systems for industrial plants.
. And this is the case not only in electric drive systems, but in general, when developing automation systems for industrial plants.
In many cases, the development of industrial plants solves the problem of ensuring the specified quality of the process while minimizing energy and economic costs. At the same time, it is necessary not only to take into account the numerous disturbing factors of the control object, but also to use several points of application of control actions.
Consider the most characteristic examples of multidimensional systems in various industries.
In fig. 3 shows the approximate structure of the installation, which implements the processing of flexible materials. Such a structure is typical for the processing of materials such as filament, wire, fabric, sheet metal, films, multilayer materials.

Fig. 3
The main objective of such systems is to stabilize the processing speed of the material. 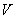 ensuring the absence of deformation of the material. To do this, the maximum number of rotating rollers is equipped with adjustable drives so that with the help of control actions - speed ratios
ensuring the absence of deformation of the material. To do this, the maximum number of rotating rollers is equipped with adjustable drives so that with the help of control actions - speed ratios 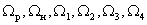 , affect linear speeds
, affect linear speeds 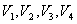 , and thus to other parameters of the material being processed, this is especially important in cases where the material is easily deformable, for example, the processing of gauze or bandages in the textile industry.
, and thus to other parameters of the material being processed, this is especially important in cases where the material is easily deformable, for example, the processing of gauze or bandages in the textile industry.
In fig. 4 shows a typical kinematic diagram of an industrial robot for manipulating and transporting objects.

Fig. four
The main task of such systems is to move the gripper arm to a given point in the working area of the robot ( 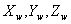 ). This task can be accomplished by acting on the angles of rotation and displacement in the joints of the manipulator (
). This task can be accomplished by acting on the angles of rotation and displacement in the joints of the manipulator ( 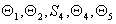 ), using electromechanical, pneumatic or hydraulic actuators.
), using electromechanical, pneumatic or hydraulic actuators.
Thus, here we also have an object and a system with a large number of input actions, that is, a multidimensional system.
The generalized structure of such multidimensional systems will have the form shown in Fig. five.
 Fig. five
Fig. five
The control generation unit (FU) converts the operator’s tasks into the system control vector 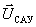 . Regulator unit (P) acting as a function of deviations of measured control variables
. Regulator unit (P) acting as a function of deviations of measured control variables 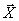 from given, manages energy converters (PE), which carry out control actions
from given, manages energy converters (PE), which carry out control actions 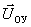 on the control object (OU). The control object is affected by disturbing influences.
on the control object (OU). The control object is affected by disturbing influences. 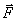 .
.
We see that in this case the multidimensional system has the vector character of the inputs, outputs, and disturbing influences, which is well illustrated in Fig. 6
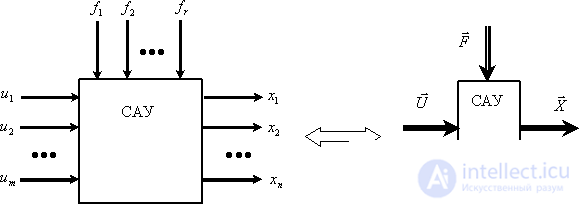
Fig. 6
In fig. 6 shows the vectors -
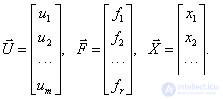
As in the case of one-dimensional (scalar) systems, we limit ourselves to considering linear control systems.
Multidimensional systems and control objects are called linear and stationary if they are described by a system of linear differential equations with constant coefficients.
Currently, in the practice of analysis and synthesis of multidimensional systems, there are two approaches to the problem of obtaining a mathematical model of such systems.
First approach
A multidimensional system is considered as a multiply connected set of dynamic links and is represented as a structural diagram or a directed graph.
Second approach
Considering the vector nature of the links between the functional elements of the ACS, when constructing mathematical models, a vector-matrix representation of equations and structural schemes describing the control object or the system as a whole is used.
Within this approach, there is a division of mathematical models into two groups.
Mathematical models in the frequency domain
They are based on the operator form of representing equations and using the Laplace transform. These are models as
matrix block diagrams
transfer matrices, sometimes referred to as equivalent matrices or input-output matrices.
Mathematical models in the time domain
They are based on the vector-matrix form of representation of systems of linear differential equations of the first order, the wide use of concepts and methods of the theory of state space.
Test questions and tasks
What automatic control system or control object is called multidimensional?
What multidimensional systems are called linear stationary?
What is the dimension of the vector of adjustable variables manipulator industrial robot shown in Fig. 4, from the point of view of the generalized structure of multidimensional systems shown in Fig. five?
What models of multidimensional objects or control systems refer to models in the time domain?
What models of multidimensional objects or control systems refer to models in the frequency domain?
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control