Lecture
Consider the problem of computing the integral of a linear integral estimate. You can first solve analytically differential equations describing the system, define the control error further, then substitute the expression for the error into the linear estimate integral and, taking it, obtain the expression for 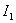 .
.
But you can do otherwise.
Let the free motion of the system regulation error be described by the equation
| (one) |
Integrating this equation -

After integration we get -
| (2) |
Upper limit substitutions are given by members of the following form -
| (3) |
since all derived errors in steady state go to zero.
Substitution of the lower limit is given by members of the form -
| (four) |
which are the initial conditions of equation (1).
Substituting (3) and (4) in (2), we get
| (five) |
And since
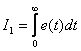 ,
,
finally get
| (6) |
Solving (6) relatively 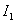 , we obtain an expression for calculating the linear integral error -
, we obtain an expression for calculating the linear integral error -
| (7) |
Now we can define 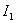 on the coefficients of the characteristic equation of the system and the initial conditions of the transition process error.
on the coefficients of the characteristic equation of the system and the initial conditions of the transition process error.
For the synthesis of systems, determining the parameters of minimizing 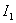 , you should use the usual methods of research functions on the extremum. Therefore, if we want to define a system parameter, for example, the parameter
, you should use the usual methods of research functions on the extremum. Therefore, if we want to define a system parameter, for example, the parameter 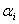 providing
providing 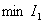 , need to decide on the parameter
, need to decide on the parameter 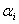 The following equation is
The following equation is
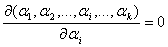 .
.
Consider a few examples of using linear integral estimation.
Example
The system has a characteristic equation
| (eight) |
Define an expression for 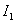 if the initial conditions are of the form -
if the initial conditions are of the form -
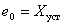 .
.
Determine the value of the parameter 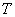 at which the integral estimate has a minimum.
at which the integral estimate has a minimum.
Decision
Denote -
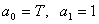 .
.
Use to find 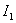 expression (7) -
expression (7) -
| (9) |
From consideration (9) we obtain that 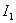 in this case it does not have an extremum, and we will receive a smaller value of the integral error with a smaller value
in this case it does not have an extremum, and we will receive a smaller value of the integral error with a smaller value 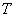 . Indeed, because equation (8) is the characteristic equation of an aperiodic link, the parameter
. Indeed, because equation (8) is the characteristic equation of an aperiodic link, the parameter 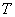 - this is the time constant. The transition process for two different time constants will have the form shown in Fig. one.
- this is the time constant. The transition process for two different time constants will have the form shown in Fig. one.

Fig. one
Example
The system has a characteristic equation
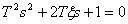 .
.
Define an expression for 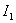 if the initial conditions are of the form -
if the initial conditions are of the form -
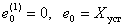 .
.
Determine the value of the parameter 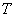 at which the integral estimate has a minimum.
at which the integral estimate has a minimum.
Decision
Denote -
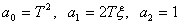 .
.
Use to find 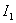 expression (7) -
expression (7) -
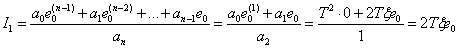 .
.
If a 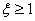 then monotonous processes
then monotonous processes 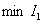 provided with the smallest
provided with the smallest 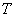 and
and 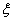 . If a
. If a 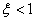 then a decrease in the attenuation coefficient decreases the linear integral estimate, but this leads to a deterioration of the transition process, an increase in its oscillatory behavior.
then a decrease in the attenuation coefficient decreases the linear integral estimate, but this leads to a deterioration of the transition process, an increase in its oscillatory behavior.
With oscillatory processes in systems, the linear integral estimate gives a significant error. At the same time, the minimum estimate can correspond to a process with a large number of oscillations with a significant amplitude, low speed, since, in fact, the evaluation involves the addition of positive and negative areas of the area under the integral curve. This is illustrated in Fig. 2 and 3, showing two processes that may have the same value of a linear integral estimate.

Fig. 2

Fig. 3
And since the form of the transition process in the analysis of the automatic control system is often unknown in advance, it is impractical to use linear integral estimates in practice.
You can try to use the integral from the error module of the following form -
| (ten) |
In fig. 4 shows an exemplary view of the error variation curves and its modulus. But the analytical calculation of the integral from the error module according to the mathematical model of the system turned out to be very cumbersome, therefore this estimate was not widely used.

Fig. four
Quadratic integral estimate
In most cases, with the possibility of an oscillatory transition process occurring in the system, a quadratic integral estimate is used, which has the following form -
| (eleven) |
Evaluation 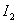 does not depend on the sign of deviations of the error, and hence on the form of the transition process, it will be monotonous, aperiodic or oscillatory in nature. In fig. 5 and 6, an exemplary view of the error variation curves and the square error is shown.
does not depend on the sign of deviations of the error, and hence on the form of the transition process, it will be monotonous, aperiodic or oscillatory in nature. In fig. 5 and 6, an exemplary view of the error variation curves and the square error is shown.

Fig. five
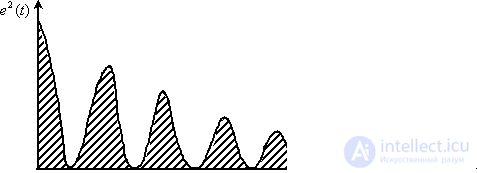
Fig. 6
Consider the procedure for calculating the quadratic estimate of the mathematical model of the system. The control system is represented as shown in Fig. 7

Fig. 7
The image of the Laplace signal at the output of the system has the form -
| (12) |
Where 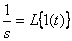 - Laplace image of a single step function - system input signal.
- Laplace image of a single step function - system input signal.
For an automatic control system, the mathematical model of which is reduced to the form (12), the integral quadratic error is determined by the following expression -
| (13) |
Where
| (14) |
at  all items with indices less than 0 and more
all items with indices less than 0 and more 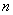 replaced by 0.
replaced by 0.
Determinants 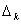 in (13) where
in (13) where 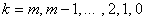 are obtained by replacing in the determinant
are obtained by replacing in the determinant  (14) (
(14) ( 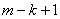 ) th column of the following column -
) th column of the following column -
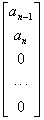 .
.
Coefficients 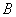 in expression (13) are defined as follows:
in expression (13) are defined as follows:
| (15) |
in determining 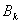 coefficients whose indices are less than 0 and more
coefficients whose indices are less than 0 and more 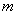 replaced by 0.
replaced by 0.
Test questions and tasks
What parameters of the mathematical model of the object are required to calculate the linear integral evaluation?
Why is it impossible to use a linear integral estimate in the case of the oscillatory nature of transients?
What integral estimates should be used in the event that oscillatory transients are possible in the system?
Give a definition of the quadratic integral estimate of the transition process.
When minimizing the quadratic estimate, what kind of transition process tends?
What parameters of the mathematical model of an object are required to calculate the quadratic integral estimate?
The control object is described by the transfer function -
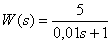 .
.
Calculate the linear integral transient estimate for the initial error value 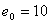 .
.
Answer :
Linear integral evaluation 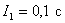 .
.
The control object is described by the transfer function -
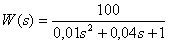 .
.
Calculate the linear integral transient estimate for the initial error value 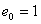 .
.
Answer :
Linear integral evaluation 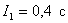 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control