Lecture
Local management tasks establish the desired nature of changes in the variables of the control object. Depending on the structure of the object, the tasks of single-channel and multi-channel control are distinguished (Fig. 1.20).
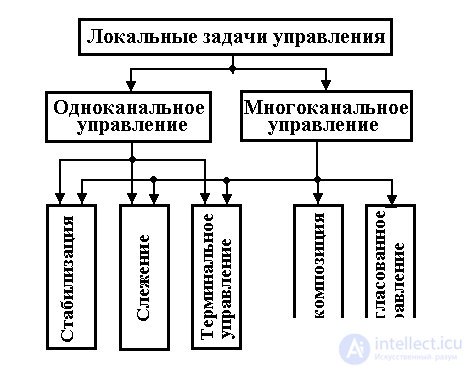
Fig. 1.20
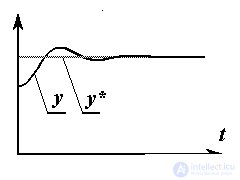
1.4.1. Single-channel control and the concept of system quality. In single-channel control problems, which include stabilization, tracking, and terminal control problems, the output variable y ( t ) is a scalar function of time.
The task of stabilization, or regulation , is formulated as the task of maintaining the output variable at a given level y *
y = y * = const.
The task of tracking is the task of observing a given law y * ( t ) of changing the variable y , i.e.
y = y * ( t ).
At the same time distinguish:
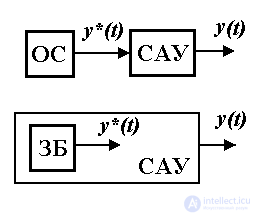 generated by a special master unit , which is part of the ACS control device.
generated by a special master unit , which is part of the ACS control device. The automatic control system that solves the tasks of tracking is called the tracking system. The signal y * ( t ), which determines the required law of motion, of the system is called the master action . Signal
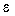 ( t ) = y * ( t ) -y ( t ),
( t ) = y * ( t ) -y ( t ), characterizing the current value of the deviation of the output variable from the driver action is called the mismatch, error, or deviation. With this value 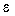 0 =
0 = 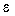 (0) = y * (0) - y (0) is the initial mismatch of the system. Then the problems of stabilization and tracking can otherwise be formulated as problems of maintaining a zero value of the mismatch, i.e.
(0) = y * (0) - y (0) is the initial mismatch of the system. Then the problems of stabilization and tracking can otherwise be formulated as problems of maintaining a zero value of the mismatch, i.e. 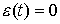 .
.
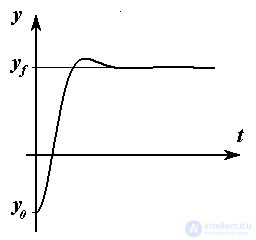
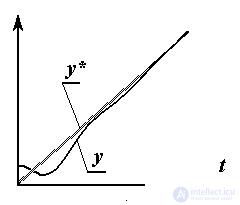
The task of the terminal control is to "move" the control object to the given (usually remote) end ( terminal ) point y f :
y  y f .
y f .
The main feature of the terminal task, which distinguishes it from the stabilization problem, is that the magnitude of the initial deviation  0 = y f - y 0 is large enough. This necessitates the choice of a specific control strategy (minimization of speed or energy costs, the need to comply with restrictions on control signals and state variables, etc.).
0 = y f - y 0 is large enough. This necessitates the choice of a specific control strategy (minimization of speed or energy costs, the need to comply with restrictions on control signals and state variables, etc.).
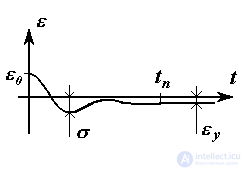
Complete elimination of mismatch 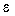 in real systems is not achieved, the reason for which are non-zero initial values
in real systems is not achieved, the reason for which are non-zero initial values 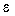 0 , the rapid changes of the setting effects y ( t ), as well as the influence of the disturbing effects f ( t ). To assess the effectiveness of solving management problems, so-called management quality indicators are introduced. There are dynamic indicators that determine the quality of the transitional mode of the system, which include quantitative (numerical) estimates of the speed and oscillation of the system, and accuracy indicators that determine the error of the system in a steady state, i.e. at the end of the transition process. The dynamic indicators include the transition time t p and the overshoot
0 , the rapid changes of the setting effects y ( t ), as well as the influence of the disturbing effects f ( t ). To assess the effectiveness of solving management problems, so-called management quality indicators are introduced. There are dynamic indicators that determine the quality of the transitional mode of the system, which include quantitative (numerical) estimates of the speed and oscillation of the system, and accuracy indicators that determine the error of the system in a steady state, i.e. at the end of the transition process. The dynamic indicators include the transition time t p and the overshoot 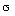 , and to accuracy - the absolute error of stabilization or tracking
, and to accuracy - the absolute error of stabilization or tracking
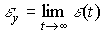 .
. 1.4.2. Multi-channel control. In multichannel problems of controlling the output of an object, there is a vector variable (output vector) y = y ( t ) = {y j ( t ) } and, therefore, the vector variables are also the specifying influence (task vector) y * = y * ( t ) = {y * j ( t ) } and mismatch (error vector) 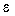 =
= 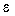 ( t ) = {
( t ) = { 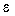 j ( t )}. The formulation of the main tasks of multichannel control (stabilization, tracking and terminal control) practically does not differ from the above. In addition to these, for multichannel objects, a number of specific tasks arise, among which we will single out the tasks of decomposition and coordinated control.
j ( t )}. The formulation of the main tasks of multichannel control (stabilization, tracking and terminal control) practically does not differ from the above. In addition to these, for multichannel objects, a number of specific tasks arise, among which we will single out the tasks of decomposition and coordinated control.
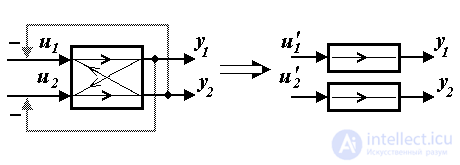
Fig. 1.21. Multi-channel system decomposition
The task of decomposition is to eliminate the mutual influence of the channels of the system in order to reduce the task of managing a multiply connected object to several simpler single-channel tasks. The solution of the problem involves the creation of additional (artificial) cross-connections between the channels of the system, which compensate for the undesirable effect of the internal connections of the control object (Fig. 1.21). This is achieved using appropriate control algorithms, i.e. selection of control actions u j .
The task of coordinated control, on the contrary, provides for the organization of forced interaction of channels in order to maintain the specified functional relationships (agreement conditions) of output variables y j (t) of the form:
(1.8) 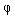 ( y 1 , y 2 , ... y m ) = 0 ,
( y 1 , y 2 , ... y m ) = 0 ,
Where 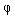 - given function of dimension m-1 . The solution also requires the introduction of artificial cross-links (Fig. 1.22), i.e. control coordination u j .
- given function of dimension m-1 . The solution also requires the introduction of artificial cross-links (Fig. 1.22), i.e. control coordination u j .
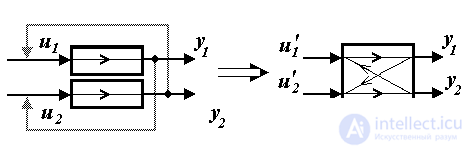
Fig. 1.22. Matching output variables
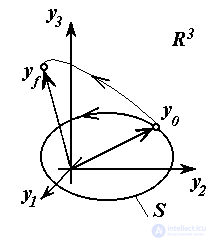 The most obvious tasks of terminal and coordinated control arise when controlling the spatial movement of multi-link mechanical objects (robots, machine tools, vehicles). Here, the Cartesian coordinates y j of the working point of the mechanism in the three-dimensional physical space R 3 or R 2 usually act as output variables of the system, and the task of moving the working point of the mechanism from the initial position y 0 = {y j0 } to the point y f = {y jf } refers to multichannel terminal tasks. If in this case it becomes necessary to follow a certain trajectory of motion S , then the problem arises of matching the output variables, in which the matching condition (1.8) is nothing but the equation S in physical space.
The most obvious tasks of terminal and coordinated control arise when controlling the spatial movement of multi-link mechanical objects (robots, machine tools, vehicles). Here, the Cartesian coordinates y j of the working point of the mechanism in the three-dimensional physical space R 3 or R 2 usually act as output variables of the system, and the task of moving the working point of the mechanism from the initial position y 0 = {y j0 } to the point y f = {y jf } refers to multichannel terminal tasks. If in this case it becomes necessary to follow a certain trajectory of motion S , then the problem arises of matching the output variables, in which the matching condition (1.8) is nothing but the equation S in physical space.
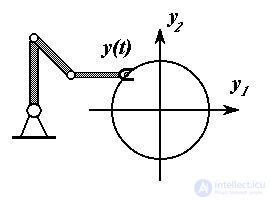
Example 1.6. The so-called contour movement of the matchmaker of the simplest manipulator in the plane R 2 is carried out along segments of straight lines and circles, given in the form
(1.9)
with 1 y 1 + with 2 y 2 + with = 0
or
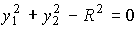 ,
, respectively. These equations determine the conditions for matching the output variables of the multichannel system under consideration.
1.4.3. Tasks control. The auxiliary tasks of determining (identifying) non-measurable variables and unknown parameters of the system are related to the tasks of automatic control. It:
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control