Lecture
Matrix structural diagrams
Matrix structural schemes are essentially a compact graphical representation of the classical structural scheme of a multidimensional object or control system. They are based on the operator form of representation of equations, on the replacement of real signals by their images according to Laplace.
Using several levels of representation of schemes that differ in the degree of aggregation (association) of links and system elements.
Let us consider different levels of representation of matrix structural schemes on the example of some generalized structure of a multidimensional automatic control system.
I level
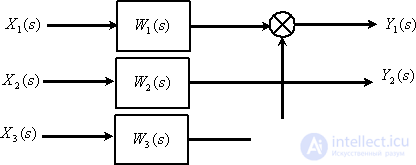
In fig. 3 are shown 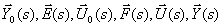 - vectors of variable images,
- vectors of variable images,

Fig. one
 ,
,
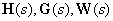 - transfer function matrices,
- transfer function matrices,
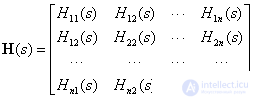 ,
,
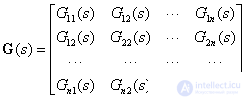 ,
,
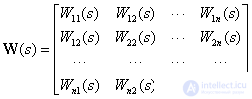 .
.
On the shown in fig. 1 matrix block diagram summing elements, matrix links and branch points perform the same functions as in conventional block diagrams. Therefore, in accordance with the scheme, you can write the system of matrix equations -

Level II
Consider the second level, assuming for the matrix structural scheme 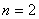 .
.

Fig. 2
Consider at this level the opamp described by the matrix 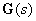
| (one) |
Let's move from matrix equations to scalar -
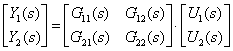 ,
,
| (2) |
The last expression shows that the transfer function  in accordance with the principle of superposition is the transfer function between
in accordance with the principle of superposition is the transfer function between 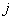 m entrance and
m entrance and 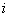 output, in the absence of signals on all inputs, except
output, in the absence of signals on all inputs, except 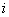 th
th
Level III
Consider the third level of matrix structural only for the control object. On the basis of the system of operator equations (2) obtained for the object, it is possible to draw a block diagram of the control object.

Fig. 3
From the proposed example of the complexity levels of the matrix structural scheme, it can be seen that the representation of even not very complex multidimensional control systems in the form of level III schemes, that is, in the form of classical structural schemes, leads to a cumbersome graphical representation that does not reflect the characteristic connections and functional elements of the system.
Transfer matrices
The transfer or equivalent matrixes refer to models of the "input-output" type and represent the matrix connecting the input and output of a multidimensional system. In fig. 4 shows a multi-dimensional system.
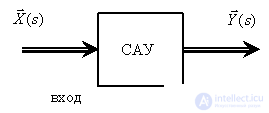
Fig. four
The matrix operator equation describing the system has the form -
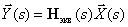 ,
,
Where 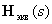 - the transfer or matrix of the system, the components of which will be the transfer functions connecting the components of the input and output vectors of the system.
- the transfer or matrix of the system, the components of which will be the transfer functions connecting the components of the input and output vectors of the system.
Analogues of equivalent matrices in one-dimensional systems are transfer functions that connect the input and output of an object or system. Matrices 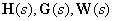 from the above matrix structural scheme (see Fig. 1) are, in fact, the transfer matrices of the multidimensional functional elements of the system.
from the above matrix structural scheme (see Fig. 1) are, in fact, the transfer matrices of the multidimensional functional elements of the system.
Equivalent matrices of multidimensional systems can be obtained in two ways.
The transfer functions that connect the respective inputs and outputs of the system are determined. That is, the matrix is determined by its components. Components are determined by known methods in accordance with the principle of superposition.
The transfer matrices are determined as a result of equivalent transformations of the matrix structural schemes or by matrix operator equations. The transformation of the matrix structural schemes is carried out in accordance with the rules of equivalent transformations of conventional structural schemes; it is only necessary to take into account the specifics of operations with vectors and matrices (non-compliance with the commutative law, replacement of division by multiplication by the inverse matrix, the concept of unit and zero matrix, etc.).
As an example, we find the transfer matrix connecting the input and output of the system considered above (Fig. 1), while we believe in accordance with the principle of superposition that the disturbance signal is absent ( 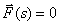 ). Then the structural diagram takes the form shown in Fig. five.
). Then the structural diagram takes the form shown in Fig. five.

Fig. five
Define 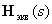 satisfying the following matrix operator equation -
satisfying the following matrix operator equation -
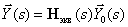 .
.
For determining 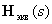 let us use the transformation of matrix operator equations, which can be written in a matrix structural diagram.
let us use the transformation of matrix operator equations, which can be written in a matrix structural diagram.
| (3) |
| (four) |
| (five) |
Substitute 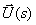 from (4) to (3)
from (4) to (3)
| (6) |
Substitute 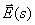 from (5) to (6)
from (5) to (6)
| (7) |
Open the brackets in the right part (7)
| (eight) |
Transfer the item with 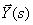 from the right side of expression (8) to the left side
from the right side of expression (8) to the left side
| (9) |
We will take out 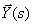 brackets to the right
brackets to the right
| (ten) |
Where 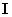 - unit matrix
- unit matrix 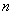 th order.
th order.
If a
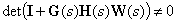 ,
,
then the matrix
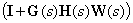 ,
,
is nondegenerate and can be obtained from the inverse matrix -
| (eleven) |
Multiply the left and right sides of equation (10) on the right by the inverse matrix (11), after simple transformations we get -
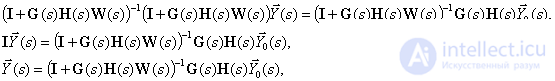
Then we finally get -
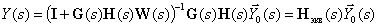 .
.
Consequently
| (12) |
By expression (12), knowing the matrix expressions for the elements of the system, one can always determine the transfer matrix of the system as a whole.
Test questions and tasks
Give the definition of a matrix structural diagram.
In what forms can matrix structural schemes be presented?
Determine the vector 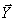 if vector
if vector 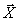 has the form -
has the form -
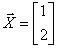 ,
,
vectors are related by the equation -
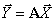 ,
,
Where
 ,
,
Answer:
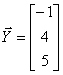 .
.
According to the matrix equation
 ,
,
define 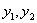 .
.
Answer:
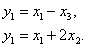
The control object is described by the transfer matrix -
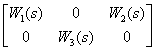 ,
,
which links vectors -

Draw a block diagram linking the components of the vectors 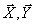 .
.
Answer:
Give the definition of the transfer (equivalent) matrix.
Define the components of the transfer matrix of the control object.
What ways can be determined transfer matrices of multidimensional objects.
For the multidimensional system shown in Fig. 1, determine the transfer matrix connecting the vectors 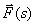 and
and 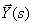 .
.
Answer:
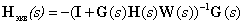 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control