Lecture
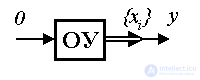
3.1.1. State variables Consider an autonomous dynamic system [M1a] with the output 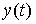 where
where 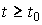 . Note that for autonomous system solution
. Note that for autonomous system solution 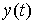 contains only free component:
contains only free component:  . We introduce variables
. We introduce variables
(3.1) 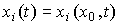 , i = 1,2, ... n
, i = 1,2, ... n
with initial values 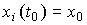 determined by
determined by 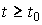 and give the following definition [7] .
and give the following definition [7] .
State variables are called linearly independent variables x i ( t ) such that their values 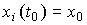 at time t 0 uniquely determine the state of the system at any time
at time t 0 uniquely determine the state of the system at any time 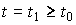 i.e. allow you to find the values of the output variable y ( t ) at arbitrary times t according to the formula
i.e. allow you to find the values of the output variable y ( t ) at arbitrary times t according to the formula
(3.2) 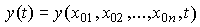 .
.
The procedure for finding the values of a function 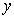 ( t ) for time points
( t ) for time points 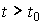 called prediction (see clause 1.1.1). The possibility of prediction is a natural requirement of quality control, which determines the importance of the introduced concept for the nonautonomous (controlled) systems considered below. At the same time, a distinctive feature of state variables is that to predict the behavior of the system at any time t > t 0 (and control a non-autonomous system) there is enough information about state variables at time t 0 and no knowledge of the process history is required, i.e. functions x i ( t ) with t < t 0. The latter serves as the basis for constructing procedures (algorithms) for forecasting and controlling dynamic systems based on the current values of state variables (see § 4.3).
called prediction (see clause 1.1.1). The possibility of prediction is a natural requirement of quality control, which determines the importance of the introduced concept for the nonautonomous (controlled) systems considered below. At the same time, a distinctive feature of state variables is that to predict the behavior of the system at any time t > t 0 (and control a non-autonomous system) there is enough information about state variables at time t 0 and no knowledge of the process history is required, i.e. functions x i ( t ) with t < t 0. The latter serves as the basis for constructing procedures (algorithms) for forecasting and controlling dynamic systems based on the current values of state variables (see § 4.3).
The state variables of an autonomous system can be chosen, in particular, the phase variables of the system, i.e. output variable y ( t ) and n-1 of its derivatives 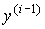 ( t )
( t ) 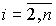 . We introduce variables
. We introduce variables
(3.3) 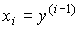 ,
, 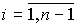
with initial values
(3.4) 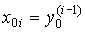 .
.
The output of the stationary autonomous system [M1a], i.e. free part of the process 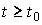 = 0, for the case of unequal roots of the characteristic equation, it is determined by the formula (see Section 2.2)
= 0, for the case of unequal roots of the characteristic equation, it is determined by the formula (see Section 2.2)
(3.5) 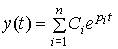 ,
,
where the coefficients C i depend on the initial values of the output variable and its derivatives, or taking into account the introduced notation:
(3.6) 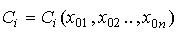 .
.
Thus, the behavior of the system under consideration  is uniquely determined by the initial values of the variables x i and, therefore, by definition, these variables are state variables. The total number of state variables is
is uniquely determined by the initial values of the variables x i and, therefore, by definition, these variables are state variables. The total number of state variables is 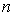 i.e. the order of the differential equation [M1a]. Linear combinations of variables x i , supplemented to an already selected set, are not state variables, since they lead to a linear dependence of the variables.
i.e. the order of the differential equation [M1a]. Linear combinations of variables x i , supplemented to an already selected set, are not state variables, since they lead to a linear dependence of the variables.
Considering the introduced notation, we transform the equation [M1a] to the normal Cauchy form. Differentiating in time the equation (3.5) and substituting the obtained expressions (3.3) and [M1a], we find the so-called equations of state of an autonomous system
(3.7) 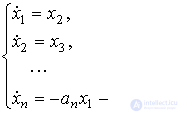
The output variable y ( t ) is related to state variables by a trivial expression ( output equation )
(3.8) 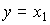 .
.
The equations of state (3.7) and output (3.8) are the simplest example of a state-output (CB) model.
Remark 3.1. The choice of dynamic state variables is ambiguous. Not only phase variables can be taken as such variables. 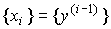 ,
, 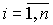 , but also physical variables of the system such as displacement, speed, current, voltage, etc. (see 4.1), as well as any other n linearly independent variables, obtained, for example, as linear combinations of phase and / or physical coordinates.
, but also physical variables of the system such as displacement, speed, current, voltage, etc. (see 4.1), as well as any other n linearly independent variables, obtained, for example, as linear combinations of phase and / or physical coordinates.
Naturally, the choice of state variables determines the structure and parameters of the state-output model. In addition to the above method of constructing such a model in the standard form (3.7), (3.8), the CB model can be obtained as a set of models of real physical processes, often corresponding to the elementary links of the first order (see Section 2.3).
3.1.2. State-output and transient models. In the most general case, the equations of state of an autonomous system are presented in the Cauchy normal form, i.e. as a system 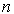 homogeneous differential equations
homogeneous differential equations
[M4a] 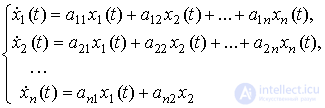
Where 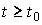 ,
, 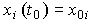 ,
, 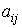 - constant or time-dependent coefficients (parameters), and the output equation relating the output variable of the system y ( t ) with the variables x i ( t ) has the form
- constant or time-dependent coefficients (parameters), and the output equation relating the output variable of the system y ( t ) with the variables x i ( t ) has the form
[M5] 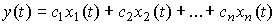 ,
,
Where 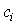 - coefficients (parameters). It is easy to show (see below) that the variables x i ( t ) are indeed state variables and, therefore, the equations [M4a] and [M5] represent the most general state-output model of a linear autonomous dynamic system.
- coefficients (parameters). It is easy to show (see below) that the variables x i ( t ) are indeed state variables and, therefore, the equations [M4a] and [M5] represent the most general state-output model of a linear autonomous dynamic system.
The vector x = x ( t ) of dimension n , whose elements are state variables x i = x i ( t ), i.e.
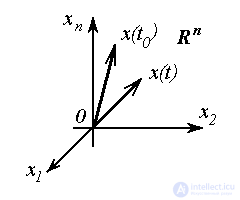
(3.9) 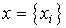 =
=  ,
,
called a state vector . The vector x is an element of n - dimensional linear (vector) space. 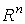 which is called the state space :
which is called the state space : 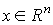
The equations [M4a], [M5] can be written in vector-matrix form:
[M6a] 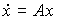 ,
,
[M7] 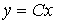 ,
,
Where 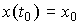 ,
, 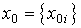 - vector of initial states (initial conditions),
- vector of initial states (initial conditions),
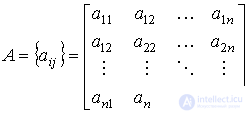 - matrix size system
- matrix size system  ,
, 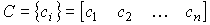 - size exit matrix
- size exit matrix 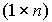 .
.
In the particular case when the equations of the BC model are presented in the form (3.7) (3.8), we get
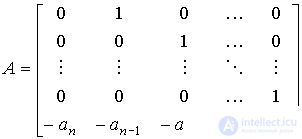 ,
, 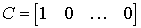 .
.
By solving a system of differential equations [M4a] with initial conditions 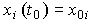 called a feature set
called a feature set
(3.10) 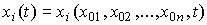 ,
,
which for t = t 0 satisfy the initial conditions, and for any 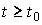 - equations [M4a]. Accordingly, the solution of the equation [М6а] will be a vector function
- equations [M4a]. Accordingly, the solution of the equation [М6а] will be a vector function
(3.11) 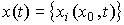 .
.
The solution can be represented as
(3.12) 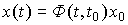 ,
,
Where 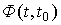 - the fundamental (transitional) matrix of the system [М6а]. Substituting (3.12) into the output equation [M7], we obtain the expression for calculating the output variable
- the fundamental (transitional) matrix of the system [М6а]. Substituting (3.12) into the output equation [M7], we obtain the expression for calculating the output variable
(3.13) 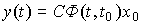 .
.
For stationary systems, the transition matrix is
(3.14) 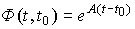 .
.
Putting 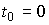 , we will find:
, we will find:
(3.15) 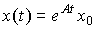
and
(3.16) 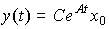 .
.
Remark 3.2. Analysis of equations (3.14) - (3.16) shows the following.
1. Output variable 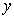 ( t ) at any time
( t ) at any time 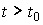 uniquely determined by n initial values
uniquely determined by n initial values 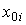 and therefore by definition the variables
and therefore by definition the variables 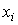 really are state variables.
really are state variables.
2. Prehistory of the system (its movement at 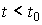 ) does not affect the behavior of the system when
) does not affect the behavior of the system when 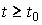 .
.
If for some initial conditions and 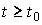 there is an identity
there is an identity
(3.17) 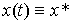 ,
,
where x * = const, then the value x = x * is called the equilibrium state , or the equilibrium position , of the autonomous system [M6a]. Obviously, in the equilibrium state,
(3.18) 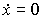
and therefore
(3.19) 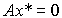 .
.
Provided that det A 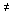 0, we find that the only equilibrium position of the [M6a] system is the origin of the state space R n , i.e.
0, we find that the only equilibrium position of the [M6a] system is the origin of the state space R n , i.e.
x * = 0,
and with det A = 0, there are nontrivial sets of equilibrium states (straight lines, planes, that is, subspaces that satisfy equation (3.19)).
After substituting x * = 0 into the output equation [M7], we find the equilibrium value of the output variable (see § 2.2.2)
y * = 0.
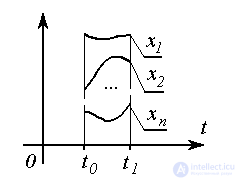
Formulas (3.14) - (3.16) determine the transient processes of the system - 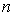 time functions
time functions 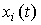 . Graphically, they can be represented as:
. Graphically, they can be represented as:
The integral curve (phase trajectory) is a line described by a state vector. 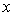 in the state space
in the state space 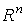 when the variable changes
when the variable changes 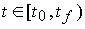 ,
, 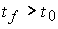 i.e. hodograph vector functions x ( x 0 , t ) by parameter
i.e. hodograph vector functions x ( x 0 , t ) by parameter 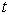 . Phase portrait - a set of phase trajectories corresponding to different values of the initial conditions
. Phase portrait - a set of phase trajectories corresponding to different values of the initial conditions 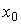 .
.
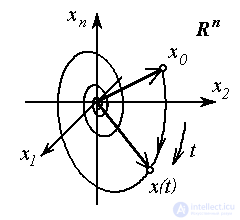
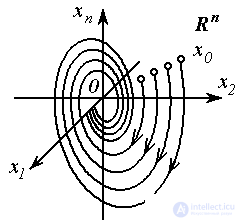
Fig. 3.1. Integral curve in R n and phase portrait
The concepts introduced above are generalized to the class of multichannel (multiply connected, see § 2.1.3) systems, which are characterized by several output variables y j , 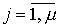 . The general model of a multichannel system includes the equations of state [M4a] and
. The general model of a multichannel system includes the equations of state [M4a] and 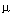 output equations
output equations
[M5m] 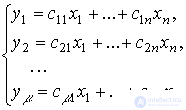
Where 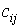 - coefficients (parameters).
- coefficients (parameters).
Define 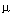 -dimensional vector of outputs
-dimensional vector of outputs
(3.20) 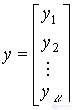
as a vector space of output variables R 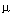 and write the equation [M5m] in a compact vector-matrix form [M7], i.e.
and write the equation [M5m] in a compact vector-matrix form [M7], i.e.
[M7m] 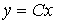 ,
,
Where 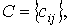 - matrix output size
- matrix output size 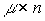 . Thus, the state-output model of the multichannel system is represented by the equations [M4], [M5m] or vector-matrix equations [M6a] and [M7m].
. Thus, the state-output model of the multichannel system is represented by the equations [M4], [M5m] or vector-matrix equations [M6a] and [M7m].
3.1.3. Properties of state-exit models . Let us analyze the solutions of the equation of state [M6a], [M7] and the associated transients of the autonomous dynamic system (3.12) - (3.16).
First we define
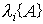 ;
; (3.21) 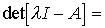
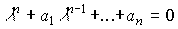 ;
;
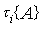 ,
, 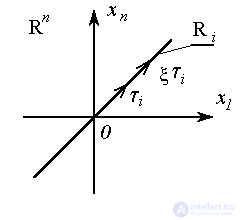
and also (for the case of real eigenvalues 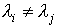 ) eigenspaces of the system as sets (straight lines, planes, etc.)
) eigenspaces of the system as sets (straight lines, planes, etc.)
(3.22) 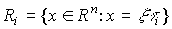 ,
,
Where 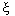 - real numbers. Recall that in this case, the eigenvectors satisfy the equations
- real numbers. Recall that in this case, the eigenvectors satisfy the equations
(3.23) 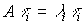 .
.
Matrix function
(3.24) 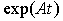 =
= 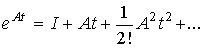
called the matrix exponent. Matrix exponent of the diagonal matrix
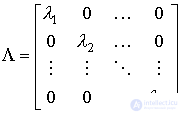 ;
;
calculated by a simple formula
(3.25) 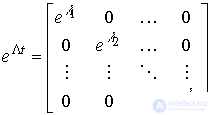 .
.
In a more general case (provided 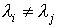 ) from the expression (3.23) we obtain:
) from the expression (3.23) we obtain:
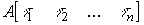
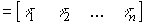
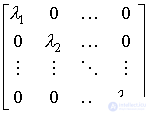
and therefore matrix A is connected to a diagonal matrix 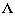 by formula
by formula
(3.26) 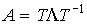 ,
,
Where
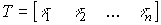 .
.
Then the matrix exponent is like
(3.27) 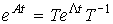 .
.
Now, taking into account equation (3.27), we rewrite the formula for calculating the state vector (3.15) as
(3.28) 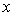
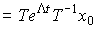
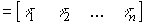
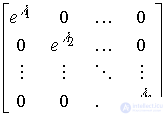
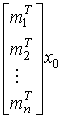 .
.
Considering that 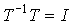 , запишем
, запишем

and therefore
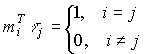 .
.
Тогда уравнение (3.28) принимает вид
(3.29) 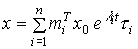 .
.
We introduce the notation
(3.30) 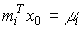 ( x 0 )
( x 0 )
и запишем формулу (3.29) в виде разложения по собственным векторам
(3.31) 
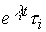 ,
,
где векторы 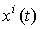 принадлежат собственным подпространствам системы
принадлежат собственным подпространствам системы 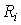 и называются собственными составляющими решения x ( t ), или модами вектора состояния системы.
и называются собственными составляющими решения x ( t ), или модами вектора состояния системы.
Замечание 3.3. Если начальное значение вектора состояния принадлежит собственному подпространству 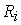 i.e.
i.e. 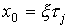 then
then
(3.32) 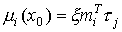
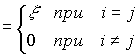
and therefore
(3.33) 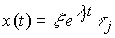
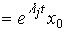 ,
,
those. траектория системы целиком лежит в собственном подпространстве R i .
Такого рода подпространства пространства состояний R n относятся к классу инвариантных множеств динамической системы.
Проанализируем поведение выходной переменной y ( t ) . Подставляя уравнение ( 3.31 ) в [M7] находим:
(3.34) 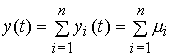
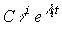 ,
,
где y i ( t ) - моды выходной переменной.
Сравнивая последнее уравнение с выражением (2.20), получим, что неопределенные коэффициенты C i могут быть рассчитаны как
(3.35) 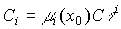 .
.
Более того,
(3.36) 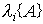 ,
,
those. полюсы системы p i совпадают с собственными числами матрицы 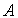 . Отсюда следует, что совпадают и характеристические уравнения (2.3) и (3.21), или
. Отсюда следует, что совпадают и характеристические уравнения (2.3) и (3.21), или
(3.37) 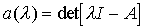 .
.
Thus, the following properties of state-output models are obtained.
Property 3.1.
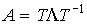 .
.
Property 3.2.
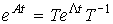 .
.
Property 3.3.
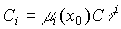 .
.
Property 3.4.
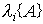 .
.
Property 3.5.
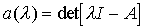 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control