Introduction Mathematical foundations of the theory of automatic control

The central concepts of the course of the theory of automatic control are the concepts of control and control system.

Management is a targeted impact on an object (a controlled process), leading to a specified change (or maintenance) of its state.

The complex (system) of interconnected elements involved in the control process is called a control system.

The concepts introduced are illustrated in fig. B.1, which presents the main elements ( blocks ) of the system and shows the nature of their interaction in the process of managing an object.

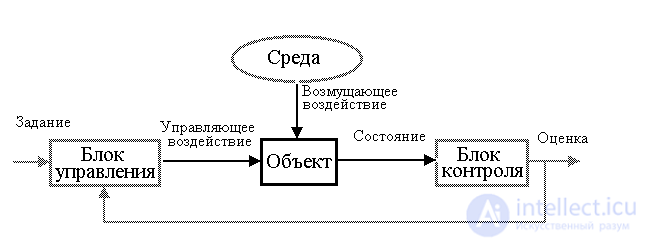
Fig. IN 1. Control system

The following types of objects and managed processes are distinguished:

• natural (natural), which include living organisms, environmental and economic processes;

• technical, i.e. mechanisms (robots, machine tools, transport), thermodynamic and chemical processes, etc.

The state of the object is characterized by some quantitative values ​​that vary over time, i.e. state variables (see § 3.1.1). In natural processes, the temperature, density, or content of a particular substance in an organism or habitat, the volume of output, the rate of securities, etc., can play the role of such variables. For technical objects, these are mechanical displacements (angular or linear) and their speeds, electrical variables, temperatures and concentrations of substances, etc.

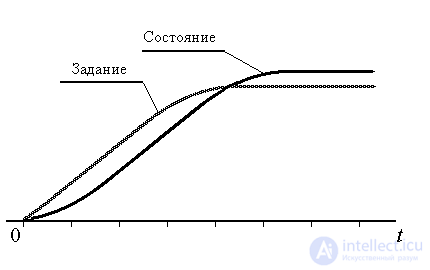
Fig. AT 2. Targeted state change

The purpose of management is to change the state of the object in accordance with a given law ( task, Fig. B.2). Such a change occurs as a result of external factors, among which are

• control (targeted) effects that ensure the execution of the task;

• disturbances that impede the desired flow of a controlled process.

Physically, the control of the object is realized with the help of control units and control units, and disturbing influences are the result of the influence of the external environment. All these blocks form the control system.

The control unit is a set of tools involved in the assessment (identification) of the state of the controlled process and / or the external environment. These tools include

• sense organs of living organisms;

• statistical services of economic systems;
• technical measuring devices (sensors);
• as well as appropriate computational tools (natural or technical) that provide the primary processing of the information received. In developed systems, the state assessment obtained as a result of the operation of the control unit is used to control the object.

A complex of interrelated elements involved in assessing the state of an object (object, control unit and external environment) is called a control system . The latter can be considered as an independent system and, at the same time, is a necessary part of the control system.

The control unit is a complex of factors that have a controlling effect on the object, taking into account the task and information about the current state of the object (assessment). The main functions of this block are reduced to information processing, i.e. are computational in nature. The control units of natural and technical systems include:

• neural systems of living organisms;
• natural regulatory factors;
• artificial means, in the role of which are both human factors (operators, organizers), and technical devices (mechanical, electrical units, computers and neural processors).

Depending on the nature of the controlled objects and other elements of the system, biological, ecological, economic and technical control systems can be distinguished. These are systems for stabilizing the temperature of living organisms and focusing the organs of vision; stabilization of the concentration of substances in organisms and gases in the atmosphere, the system of management of trade enterprises, the stabilization of the rate of securities and the regulation of supply and demand. As examples of technical systems of various levels of complexity can be cited:

• discrete action systems, or automata (shopping, games, music);

• sound, image or magnetic recording leveling systems;

• control systems of the spatial movement of the working mechanism of the machine or robot, the mechanisms of the vehicle;

• aircraft control systems, which include the ACS of engines, steering mechanisms, autopilots and navigation systems;

• aerospace complexes that solve complex tasks of the organization (control) of flights.

The main subject of the theory of automatic control are automatic control systems, automatic control systems, and, in part, automated systems.

Automatic control systems (ACS) and automatic control are technical and natural systems that perform their functions automatically, i.e. without the conscious participation of man.

An automated system is a system, part of the functions of which is performed automatically, and partly by the operator (organizer).

Mathematical foundations of the theory of automatic control (MOTAU) is an academic discipline included in the curriculum:

• • training graduates with qualifications engineer in the direction of training 654500 "Electrical Engineering, Electromechanics and Electrical Engineering" educational program (specialty) 180400 "Electric drive and automation of industrial plants and technological complexes", cycle of natural science and mathematical disciplines, national-regional (university) component, code EH .P.00;

  • training of bachelors of engineering and technology in the direction 551300 "Electrical Engineering, Electromechanics and Electrical Engineering", the cycle of natural science and mathematical disciplines, the national-regional (university) component, the code EN.P.00.

The purpose of teaching the discipline is to give students a fairly complete picture of the basic concepts and principles of obtaining, transforming and analyzing various types of mathematical models used in the theory of automatic control to describe control objects of various nature and control systems of various classes. In addition, students should master the skills of solving practical problems related to mathematical modeling in the theory of automatic control, rationally using the mathematical apparatus.

A wide range of methods for analyzing and synthesizing automatic control systems, various forms of representing mathematical models of objects of different nature, used by specialists and bachelors, requires the following tasks to be solved within the MOTAU discipline:

• • the deepening of knowledge and the formalization of representations in the field of the foundations of the mathematical description of automatic control systems, such sections of higher mathematics as fractional rational functions of a complex variable, impulse functions, Fourier and Laplace transforms, an operator method for solving differential equations, linear algebra;

  • the formation of knowledge and practical skills of obtaining and transforming various forms of mathematical models of dynamic units and automatic control systems in order to use them rationally in solving problems of analysis and synthesis of control systems;

  • studying the specifics of the methods of obtaining and transforming mathematical models of multidimensional control objects based on the apparatus of linear algebra and the representation of objects in the state space;

  • the study of methods for assessing the quality of processes in automatic control systems, the formation of practical skills in the use of various quality criteria for transients in the analysis and synthesis of automatic control systems;

  • the formation of concepts and practical skills in solving problems of the identification of elements of ACS.

The study of the discipline is based on the fact that the student has relevant mathematical training in the field of differential and integral calculi, linear algebra, complex numbers and trigonometric functions, as well as is familiar with the basic concepts and laws discussed in the courses of theoretical fundamentals of electrical engineering and theoretical mechanics. Education in the 4th semester takes place in parallel with the study of TOE (part 2), in the 5th semester - with the study of TAU (part 1).

The discipline is designed to study during the 4th and 5th semesters (2nd and 3rd year), includes 42 lecture hours, 28 hours of practical training and 14 hours of laboratory practical work.

The discipline includes the following main sections:

• basics of mathematical description of automatic control systems,

• types of mathematical models of dynamic links

• mathematical models of elementary dynamic links,

• mathematical models of ACS,

• features of mathematical models of multidimensional automatic control systems,

• methods for assessing the quality of automatic control systems,

• identification of the parameters of the mathematical model of automatic control systems.