Example of transfer function modeling

Consider an example of modeling with the gain K = 8 and the time constant of the aperiodic link T = 4. The transfer function of a closed system in this case takes the following form:

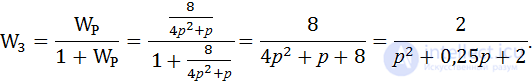
Roots of the characteristic equation

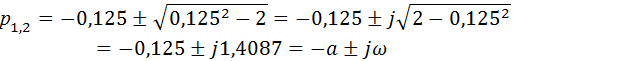
Processes in such a system will be oscillatory in nature with a frequency f and a period t of natural oscillations

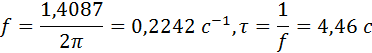
The time constant from which the amplitude of oscillation decreases is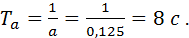

Based on the obtained calculation results, we set the integration time equal to 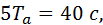and the maximum step is chosen less than the oscillation period of more than 40 times and equal to 0.1 s.

In the integration block, we set the initial deviation in X equal to 10. Accordingly, in the XY_Graf block we set the deviations in X , also equal to 10, and along the Y axis 1.4 times more and equal to 15.

Further on fig. 5.2 shows the result of modeling as a transient as a function of time, and Figure 3 shows the phase trajectory of this process. Figure 4 shows the phase portrait of the system, based on the results of modeling four transients with corresponding initial deviations.

According to the simulation results we can conclude:

a) the nature of the transient processes is indeed oscillatory,

b) the control system is stable,

c) the phase portrait consists of trajectories in the form of narrowing ellipses with a stable focus at the equilibrium point.

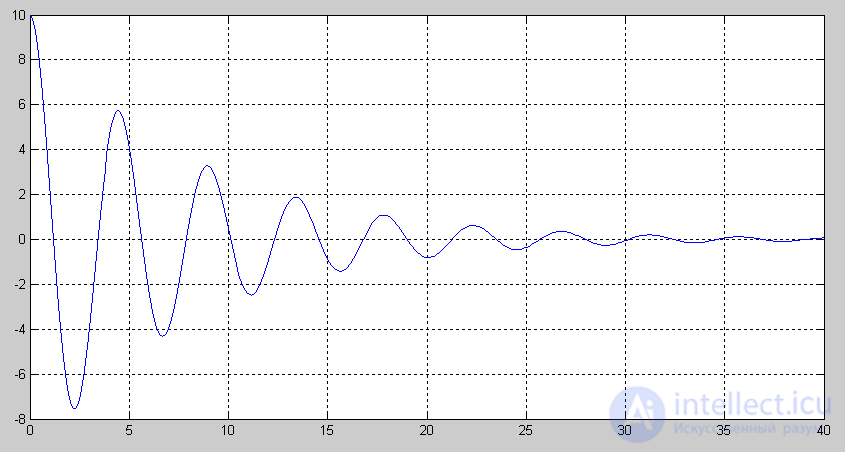
Fig. 5.2. The transition process in the system when the deviation X = 10.

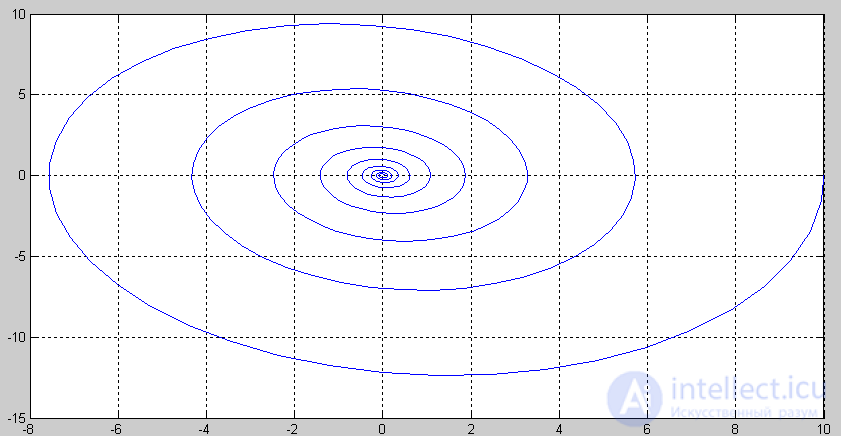
Fig. 5.3. Phase trajectory at initial deviation X = 10

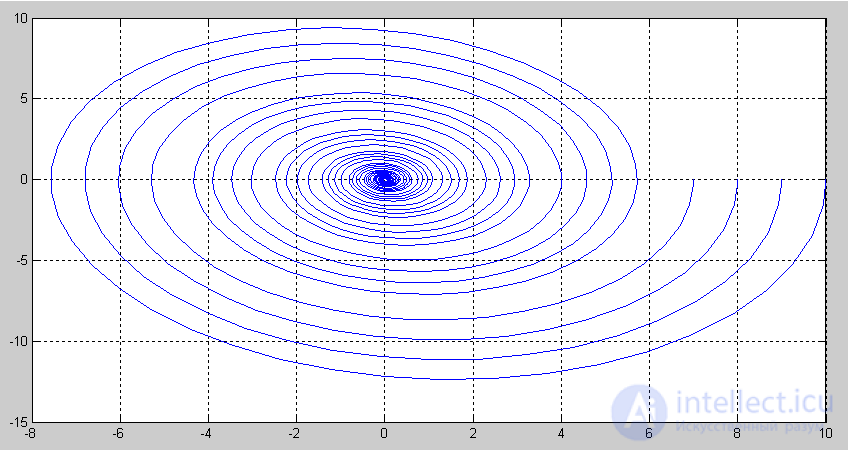Fig. 5.4. Phase Porting Automatic Control System