Lecture
Any linear ACS can be represented as a transfer function in the form of a Bode.
 ,(one)
,(one)
Where 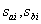 can be either real or complex conjugate. Consider separately each case.
can be either real or complex conjugate. Consider separately each case.
Valid Zeros and Poles
We transform the factors from (1) by entering the notation
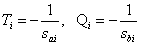 ,
,
as a result, we have factors of the following form -
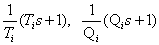 (2)
(2)
Complex conjugate zeros and poles
In this case, we have the roots of the form -
 ,
,
and their corresponding factors
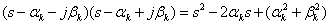 .
.
We introduce the notation -
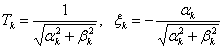 ,
,
we obtain the factors of the following form
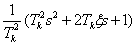 , (3)
, (3)
in the numerator and denominator of the transfer function.
Then (1) with regard to (2) and (3) can be written in the following form
as a result, we have factors of the following form -
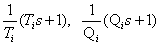 . (2)
. (2)
Complex conjugate zeros and poles
In this case, we have the roots of the form -
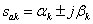 ,
,
and their corresponding factors
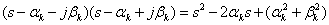 .
.
We introduce the notation -
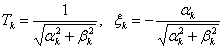 ,
,
we obtain the factors of the following form
 , (3)
, (3)
in the numerator and denominator of the transfer function.
Then (1) with regard to (2) and (3) can be written in the following form
 ,(four)
,(four)
Where
 .
.
From (4) it follows, taking into account the rule of equivalent transformation of structural schemes, that a linear ACS can be represented as a serial connection of elementary dynamic links of the 1st and 2nd order with transfer functions of the following form
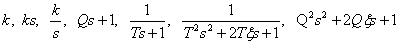 .(five)
.(five)
In addition, the transfer function of the ACS can be represented in the form of Hevisite -
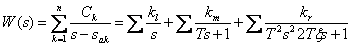 .
.
From which it follows that the ACS can be represented as parallel-connected links with transfer functions of the form (5). In addition, the transfer functions of the 1st and 2nd order describe many functional components of the control systems.
Such dynamic links are called elementary or typical links, the study of their properties and characteristics gives a lot in the synthesis and analysis of real and complex systems.
Typical links include the following dynamic links:
Inertialess (scaling, proportional) link
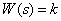 .
.
Differentiator link
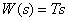 .
.
Integrating link
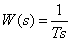 .
.
Aperiodic link
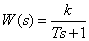 .
.
Oscillatory link
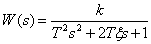 .
.
Boost links
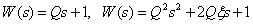 .
.
Comment
The following links are not elementary in the full sense of the word, but they are often classified as typical due to their wide distribution.
Real differentiating link
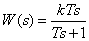 .
.
Integral with delay
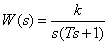 .
.
Proportional-integral link
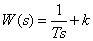 .
.
The characteristics (time and frequency) of typical links can be obtained analytically from their transfer functions, while it is convenient to use a summary diagram showing the relationship of mathematical models of dynamic links.

Fig. one
Instant link
Transmission function
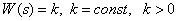 .
.
Time characteristics
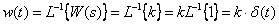 ,
,
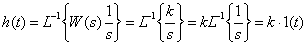 .
.

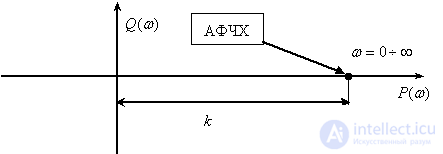
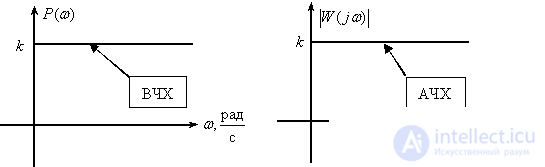
Frequency response
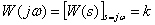 ,
,
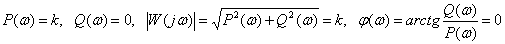 .
.
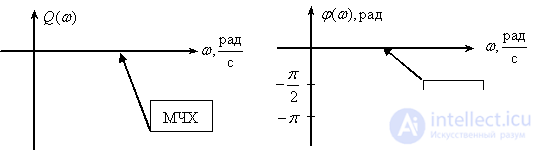
Differentiator link
Transmission function
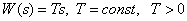 .
.
Time characteristics
 ,
,
 .
.
Frequency response
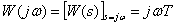 ,
,
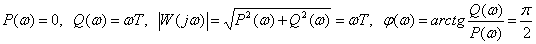 .
.

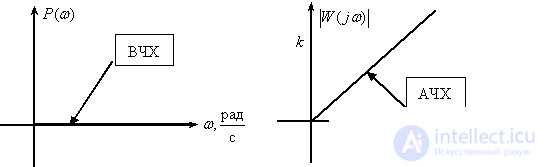
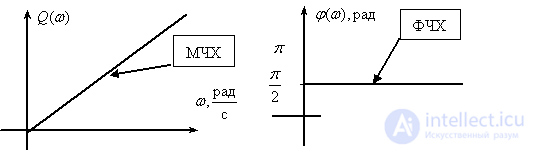
Integrating link
Transmission function
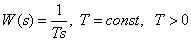 .
.
Time characteristics
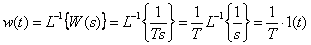 ,
,
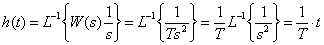 .
.

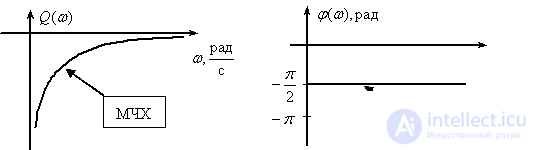
Frequency response
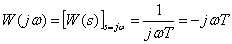 ,
,
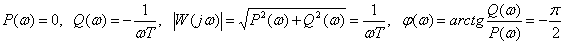 .
.


Test questions and tasks
Give the definition of a typical dynamic link.
Why do typical dynamic links study in such detail?
List the dynamic links that are classified as typical (elementary).
How to determine the impulse response of a dynamic link from the transfer function?
How to determine the transient characteristic of a dynamic link by transfer function?
How to determine the frequency response of a dynamic link from the transfer function?
What type of link shifts the harmonic signal of any frequency at an angle 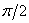 towards the delay?
towards the delay?
What type of link shifts the harmonic signal of any frequency at an angle 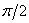 in the direction of advance?
in the direction of advance?
What type of link does not change the phase of the harmonic signal of any frequency?
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control