Lecture
Above were considered mathematical models of individual dynamic links. The ACS is a system consisting of functional elements, each of which can be represented as a dynamic link. That is, ACS can be represented as a set of dynamic links with well-known mathematical models. Consider the structure of a typical ACS -
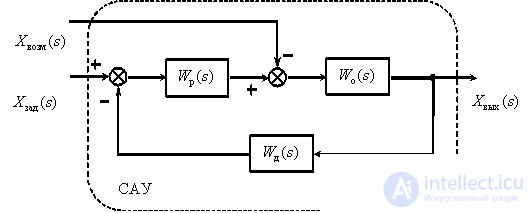
Where 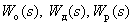 - the transfer functions of the object, sensor and regulator, respectively,
- the transfer functions of the object, sensor and regulator, respectively,  - images of the specifying, disturbing and output signals.
- images of the specifying, disturbing and output signals.
In the process of analysis and synthesis of the ACS, it is necessary to obtain the transfer functions of the ACS, which associate the output variable with the task and the perturbation in the ACS, according to the known structural scheme and transfer functions of the dynamic links included in the ACS.
A similar problem arises when the frequency characteristics of dynamic links are known, and it is necessary to determine the frequency characteristics of the ACS that characterize the relationship between the output and the input of the ACS.
The solution of these problems we will do in the future.
This problem is solved by converting (folding) the structural scheme to a single dynamic link with the desired transfer function based on the use of the rules of equivalent transformations of structural schemes and the principle of superposition (superposition).
The rules of equivalent transformations make it possible to find the necessary transfer function of the ACS by turning the block diagram to a single dynamic link with the desired transfer function.
Consider the rules of equivalent transformations that do not change the properties of the systems and are necessary for finding the transfer function:
Consecutive connection of dynamic links.
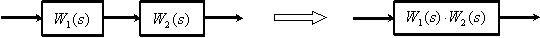
Parallel connection of dynamic links.
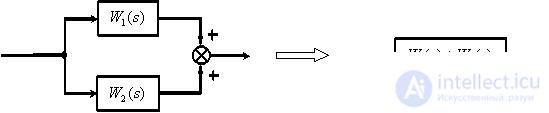
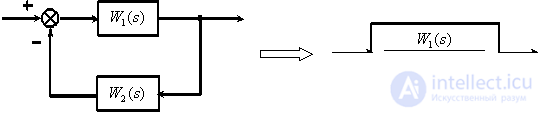
Closed loop with negative feedback.
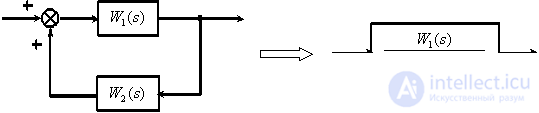
Closed loop with positive feedback.
Transfer of a branch point through a dynamic link.
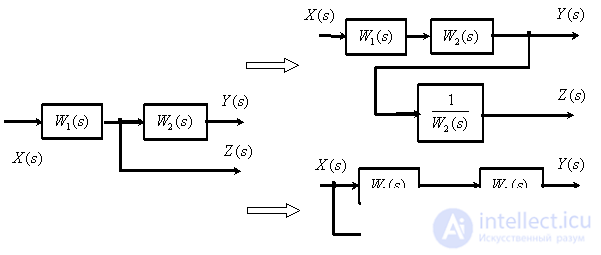
Transfer summing link through a dynamic link.
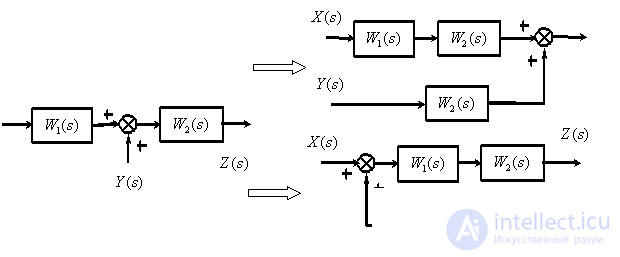
Rearrange the summing links.

Transfer of the branch point from the output to the input of the summing element.
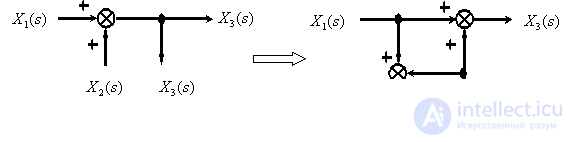
Transfer of the branch point from the input to the output of the summing element.
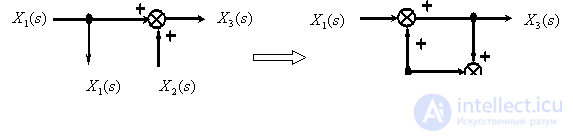
The principle of superposition (overlay)
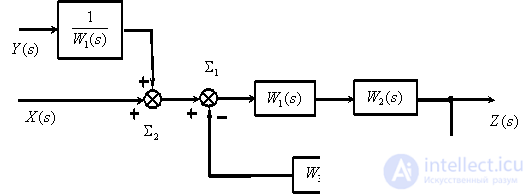
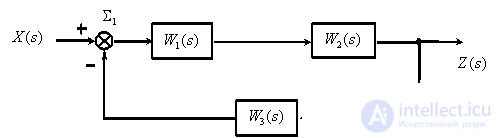
Apply the rules discussed to simplify the structural scheme.
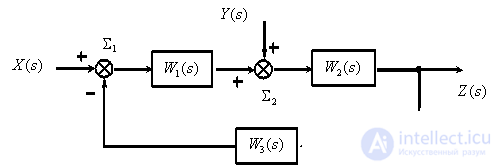
Fig. one
The transformation process, which is often called the collapse of the structural scheme, is as follows.
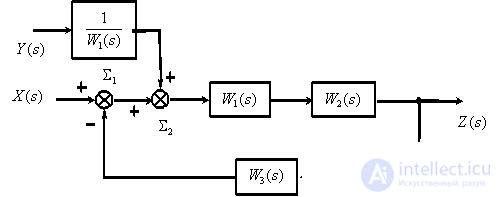
Migrate Summing Link 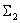 via dynamic link
via dynamic link 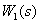 .
.
Swap the summarizing links 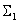 and
and 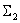 .
.
Convert the consecutive dynamic links 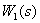 and
and 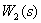 .
.
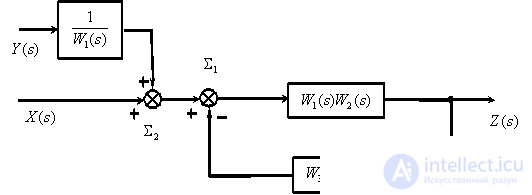
Transform a closed loop with negative feedback (  ).
).
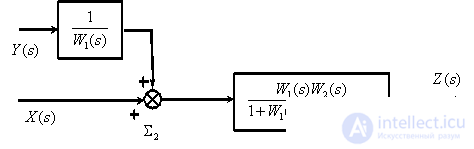
Migrate Summing Link  to the right.
to the right.
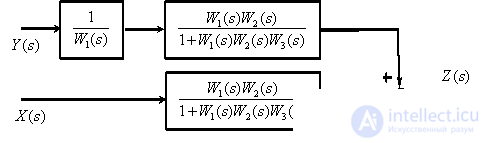
Convert the consecutive links ..
In accordance with the obtained structural scheme, we write the operator equation -
| (one) |
Equation shows that 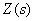 is a linear combination of images of input signals taken with coefficients
is a linear combination of images of input signals taken with coefficients 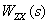 and
and 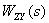 . Let us clarify the meaning of these coefficients by the example of the coefficient
. Let us clarify the meaning of these coefficients by the example of the coefficient 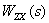 . For this we put in (1)
. For this we put in (1) 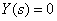 , then we get -
, then we get -
| (2) |
Thus, from (2) it follows 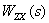 - this is the transfer function of the dynamic link, to which the structural scheme is rolled up on the assumption that the images of all input signals, except
- this is the transfer function of the dynamic link, to which the structural scheme is rolled up on the assumption that the images of all input signals, except 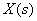 , are equal to zero.
, are equal to zero.
Now it becomes clear the meaning of the operator equation itself (1), which describes the system. It consists in the fact that the response of a linear system to the jointly acting input signals can be defined as the sum of partial reactions, each of which is calculated under the assumption that only one input signal acts on the system, and the others are zero.
In essence, this is the formulation of a fundamental principle, which is called the principle of superposition or superposition. This principle can be considered as an addition to the rules of equivalent transformations of structural schemes and actively used in practice.
Practically, the principle of superposition to find a specific transfer function is used as follows. All input signals are assumed to be equal to zero, except for the required signal, and then the structural circuit is transformed into one dynamic link.
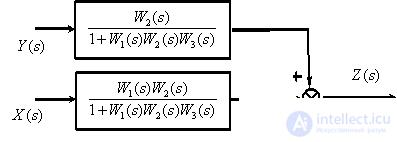
Consider the use of the principle of superposition on the example shown in Fig. 1 block diagram.
Suppose 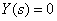 and draw the corresponding to this case block diagram.
and draw the corresponding to this case block diagram.
Using equivalent transformations, we get -
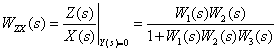 .
.
Suppose 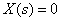 and draw the corresponding to this case block diagram.
and draw the corresponding to this case block diagram.
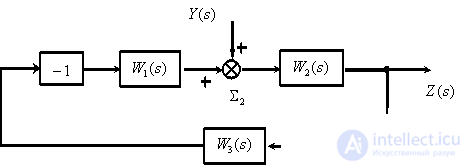
Using equivalent transformations, we get -
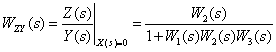 .
.
Having 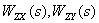 , in accordance with the principle of superposition, we obtain a "collapsed" structural scheme of the ACS.
, in accordance with the principle of superposition, we obtain a "collapsed" structural scheme of the ACS.

Test questions and tasks
What tasks allow solving the rules of equivalent transformations of structural schemes?
Define the principle of superposition as applied to block diagrams of automatic control systems.
How to use the principle of superposition in practice?
Identify transfer functions
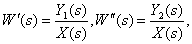
according to the following structural diagram
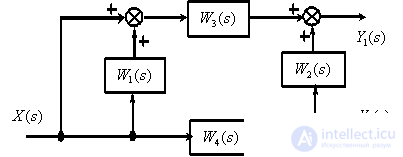
Answer :
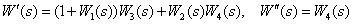 .
.
Determine the transfer function equivalent to the block diagram.

Answer :
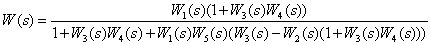 .
.
Identify transfer functions
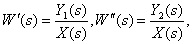
according to the following structural diagram

Answer :
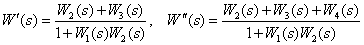 .
.
Identify transfer functions
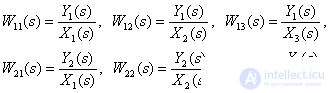
according to the following structural diagram

Answer :
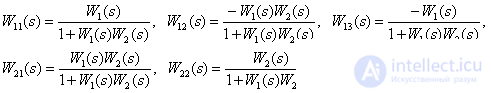
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control