Lecture
The concept of linear dynamic link
ACS is conveniently presented for analysis and in the synthesis in the form of an interconnected set of separate elements - dynamic links.
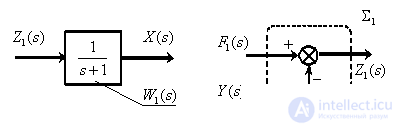
The dynamic link is generally understood as an abstract device that has an input and an output, and for which an equation is given that relates the input and output signals, as shown in Fig. one.
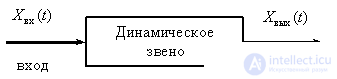
Fig. one
A detailed study of the properties of real control objects and automatic control systems leads to the description of dynamic links in the form of nonlinear differential equations. But in many cases they can be linearized, that is, non-linear equations can be replaced by linear ones, approximately describing the processes in the systems. Thus, the decomposition of the problems of analysis and synthesis of systems is carried out, that is, they initially use a linear representation and then take into account the features introduced by the nonlinearities. This approach contributes to the fact that, in most cases, a normally functioning system operates in the mode of small deviations, in which nonlinearities do not appear. In the future, we will mainly consider the apparatus for studying linear systems, and the features of systems of other classes: nonlinear, pulsed, digital, and stochastic will be presented later in other academic disciplines.
If the equation linking the signals 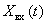 and
and 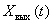 linear, then we speak of a linear dynamic link
linear, then we speak of a linear dynamic link
The equation of a linear dynamic link has the following general form:
|
|
(one) |
Where 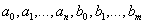 - constant coefficients
- constant coefficients 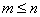 .
.
It is not rational to use such a description of a dynamic link in problems of analysis and synthesis of systems and control objects, therefore there are other forms of description and representation of dynamic links and systems as a whole.
Transmission function
Subject equation (1) to the Laplace transform, assuming the initial conditions are zero and replacing the original signals with Laplace images
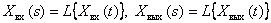 .
.
Using the theorems of the Laplace transform of linearity and differentiation, we obtain an operator equation relating the images of the input and output signals
|
|
(2) |
Transform equation (2) to the following form
|
|
(3) |
We obtain from (3) the ratio of the images of the output and input signals
|
|
(four) |
The ratio (4) does not depend on the signal images, is determined only by the parameters of the dynamic link itself ( 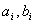 ), has the form of a fractional rational function.
), has the form of a fractional rational function.
The ratio of images of the output and input signals is called the transfer function of the dynamic link.
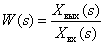 .
.
Equation of the form
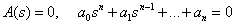 ,
,
is called the characteristic equation of a dynamic link, since the denominator of the transfer function is the characteristic polynomial of a differential equation that describes a dynamic link.
Example
Determine the transfer function of the dynamic link on its circuit diagram

Fig. 2
Solution :
According to the second Kirchhoff law, we write the equations describing the scheme
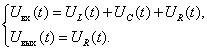
Given that
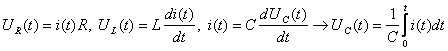 ,
,
we get
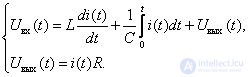
We obtain operator equations
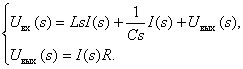
From the second equation we express the value of the current image
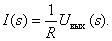
Substitute the resulting expression in the first equation of the system
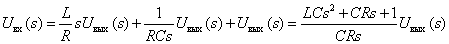 .
.
As a result, we obtain the desired transfer function
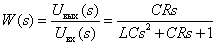 .
.
Structural scheme
Graphically, the transfer functions of the dynamic link are as follows:
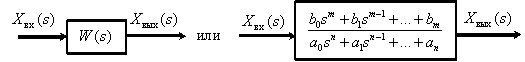
Fig. 3
If you know the image of the input signal and the transfer function of the dynamic link, you can always find the image of the output signal at zero initial conditions
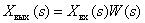 .(five)
.(five)
In the general case, the ACS consists of a set of dynamic links, the signals from the outputs of the links can be summed or subtracted, summed with signals external to the ACS. Summation and subtraction of signal images can be represented graphically using summing links:
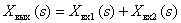
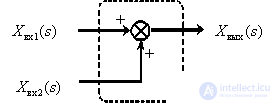
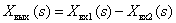

The above ambiguity of the graphical representation of the subtraction of images on the summing element is associated with differences in standards from different countries.
Using a graphical representation of the transfer functions of links and summing links, one can graphically represent the operator equations describing the ACS. Such a graphical representation of operator equations in TAU is called a block diagram.
Example
According to the mathematical model of the control object in the form of a system of differential equations to determine the structural diagram of the object.
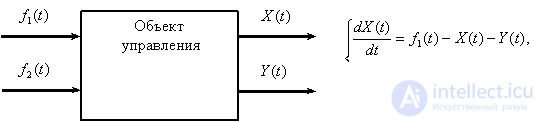
Solution :
We obtain a system of operator equations, subjecting the original system of differential equations to the Laplace transform and replacing the originals with images,
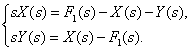
From the first equation of the system of operator equations, which describes the dynamic link of the control object, after transformations we get
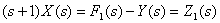 .
.
Then the transfer function of this link has the form
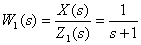 ,
,
and the expression 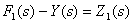 describes the summing link
describes the summing link  . Thus, two fragments of the structural scheme were obtained.
. Thus, two fragments of the structural scheme were obtained.
From the second equation of the system of operator equations, which describes the dynamic link of the control object, after transformations, we obtain, by entering the notation,
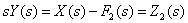 .
.
Then the transfer function of this link has the form
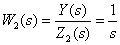 ,
,
and the expression 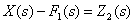 describes the summing link
describes the summing link 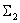 . Thus, two more fragments of the structural scheme were obtained.
. Thus, two more fragments of the structural scheme were obtained.
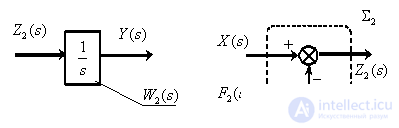
Let's connect all the fragments of the structural scheme of the control object, combining the same-named signals, or branching them with the help of the branch points shown in the diagram. As a result, we get

Dynamic characteristics of the dynamic link
The temporal or impulse response of a dynamic link is the link’s response to  denoting it as
denoting it as  . In this scheme of the experiment has the form -
. In this scheme of the experiment has the form -
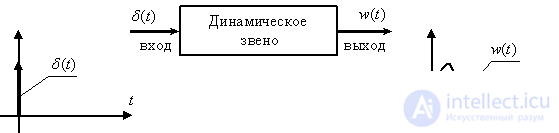
Fig. four
Let us find out what is the temporal characteristic, that is, why is it called the characteristic of the dynamic link?
To do this, consider the dynamic link with the transfer function 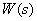
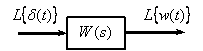
Fig. five
In this case, in accordance with (5), we have
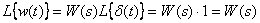 .
.
In this way
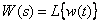
We obtain that the transfer function of a link is a Laplace image of the impulse response of a dynamic link. In turn, the impulse response can be determined by the transfer function
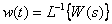 ,
,
when using decomposition in the form of Heavisite and the inverse Laplace transform.
Knowledge of the impulse response makes it possible to determine the response of a dynamic link to a signal of any shape.
For dynamic link with transfer function 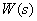 transform (5), using the theorem on multiplication of images of the Laplace transform,
transform (5), using the theorem on multiplication of images of the Laplace transform,
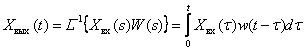 ,
,
and if it is easy to get 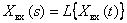 then
then
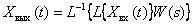 .
.
The transitional characteristic or transitional function of a dynamic link is the reaction of a dynamic link to  denoting it as
denoting it as  . In this scheme of the experiment has the form -
. In this scheme of the experiment has the form -
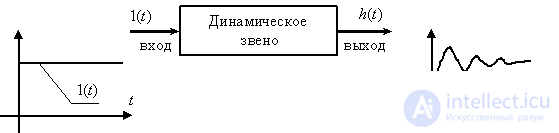
Fig. 6
To analyze the transient response, we consider a dynamic link with a transfer function. 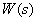
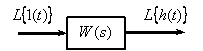
Fig. 7
In this case, in accordance with (5), we have
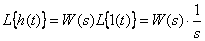 .
.
By the theorem on the integration of the original, we have
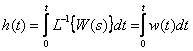
The transition function is the time integral of the impulse response and vice versa.
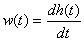 .
.
The transient response of a dynamic link can be determined from the transfer function.
Test questions and tasks
What is a linear dynamic link?
How to determine the transfer function of a linear dynamic link?
List the main elements of structural diagrams of control systems.
How to determine the temporal characteristics of a dynamic link transfer function: pulsed and transient?
How to determine the impulse response of a dynamic link from the transient response?
Determine the transfer function of the dynamic link on its circuit diagram

Answer :
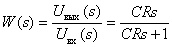 .
.
Determine the transfer function of the dynamic link on its circuit diagram
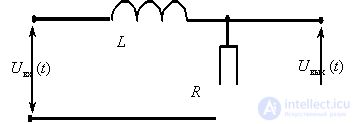
Answer :
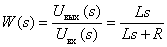 .
.
According to the mathematical model of the control object in the form of a system of differential equations to determine the structural diagram of the object.

Answer :
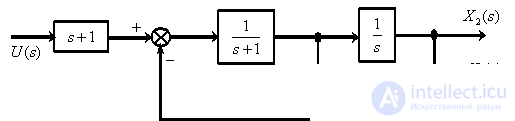
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control