Lecture
Formulas used in solving
The transfer function of the control for an open system:
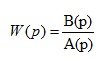 (3.1)
(3.1)
Disturbing transfer function for an open-loop system:
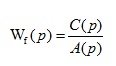 (3.2)
(3.2)
The transfer function of the control for a closed system:
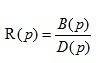 (3.3)
(3.3)
The transfer function of the disturbing effects for a closed system:
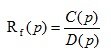 (3.4)
(3.4)
The transfer function of the control for the error:
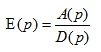 (3.5)
(3.5)
Disturbance transfer function for error:
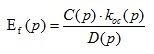 (3.6)
(3.6)
A (p) - Polynomial open automatic system
B (p) - Polynomial control action of an open automatic system
C (p) - Polynomial disturbing effect of an open automatic system
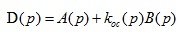 (3.7)
(3.7)
D ( p ) is the characteristic polynomial of a closed automatic system.
The equations for an open automatic system, for a closed automatic system and for an error:
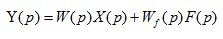 (3.8)
(3.8)
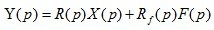 (3.9)
(3.9)
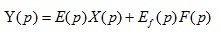 (3.10)
(3.10)
The characteristic polynomials of the open A (p) and closed D ( p ) systems, as well as the roots of the corresponding characteristic equations, play an important role in the study of the dynamic properties of speakers.
Transfer functions 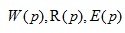 they are called the main or main operators of the automatic system, since they completely determine the dynamic and accuracy characteristics of the system.
they are called the main or main operators of the automatic system, since they completely determine the dynamic and accuracy characteristics of the system.
Transfer functions 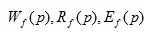 They are not the main operators, as they depend on the point of application of the disturbing action.
They are not the main operators, as they depend on the point of application of the disturbing action.
In practical studies of the automatic system, you need to know the links between the main operators:
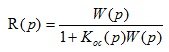 (3.11)
(3.11)
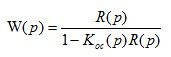 (3.12)
(3.12)
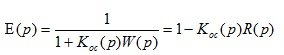 (3.13)
(3.13)
Thus, it is enough to know one of the main operators and the transfer function of feedback 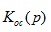 to define all the other main operators.
to define all the other main operators.
Example 1. Make an equation of the automatic control system, the scheme of which is shown in Figure 3.1:

Fig. 3.1. Structural scheme
Decision:
Determine the transfer function W (p) of an open-loop system for a given influence and the transfer function of the system W f (p) for a disturbing effect:
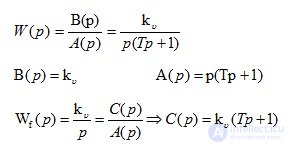
Define the transfer function R (p) of the closed-loop system for the control action and the transfer function R f (p) of the closed-loop system for the disturbing influence:
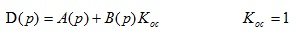
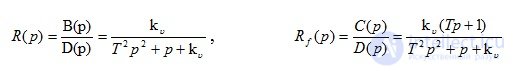
Define the transfer function for the error on the main impact of E (p) and the transfer function of the error on the disturbing influence of E f (p):
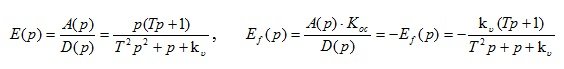
Knowing the transfer functions, you can write any equation of the system:
a) Equation of a closed automatic system:
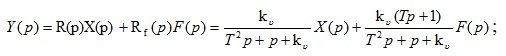
b) Equation of an open automatic system:
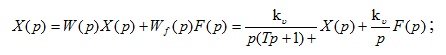
c) Error equation:
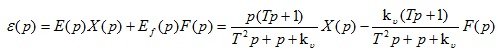 .
.
The well-known analogy between transfer functions and transfer operators allows one to compose equations of automatic systems not only in Laplace images, but also differential equations.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control