Lecture
Aperiodic link
Transmission function
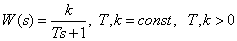 .
.
Time characteristics
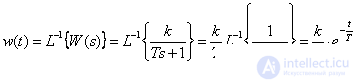 ,
,
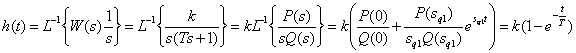 .
.

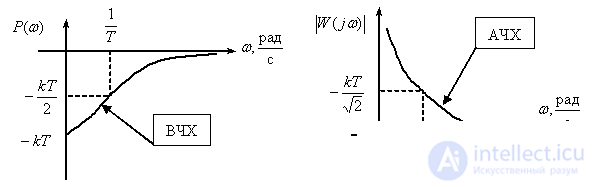
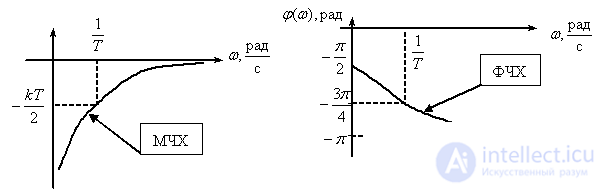
Frequency response
 ,
,
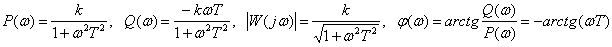 .
.
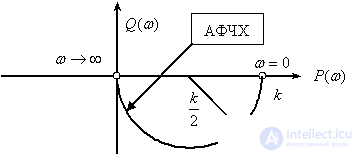
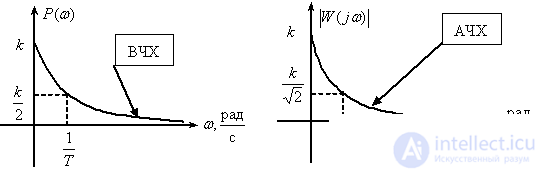
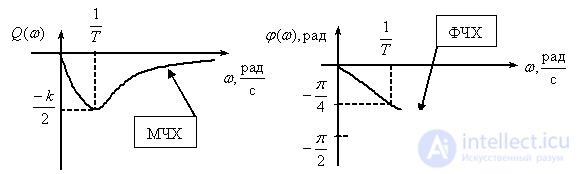
Real differentiating link
Transmission function
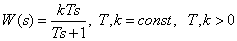 .
.
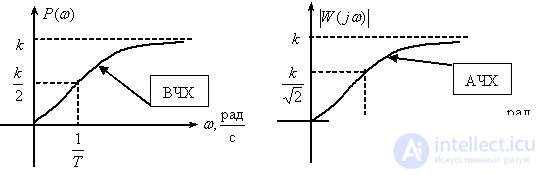
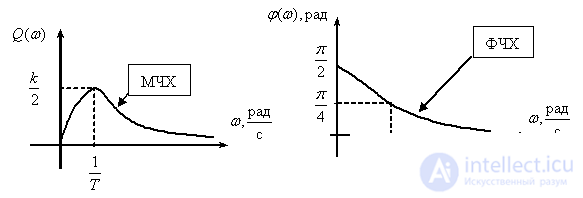
We transform the transfer function of a real differentiating link for the convenience of obtaining temporal characteristics -
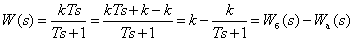 .
.
Temporal characteristics can be determined by the known characteristics of the inertialess and aperiodic links -
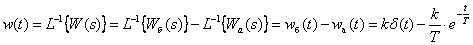 ,
,
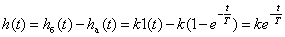 .
.

Frequency response
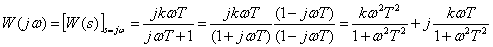 ,
,
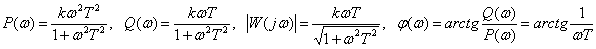 .
.

Integrated Link with Lag
Transmission function
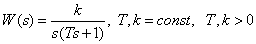 .
.
We transform the transfer function of a real differentiating link for the convenience of obtaining temporal characteristics -
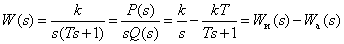 ,
,
Where
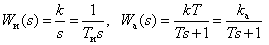 .
.
Temporal characteristics can be determined by the known characteristics of the integrating and aperiodic links -
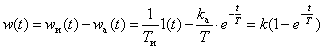 ,
,
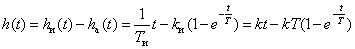 .
.

Frequency response
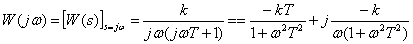 ,
,
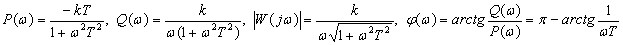

Proportional-integrating link
Transmission function
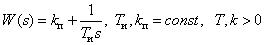 .
.
Temporal characteristics can be determined by the known characteristics of the inertialess and integrating links -
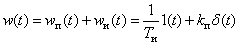 ,
,
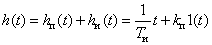 .
.

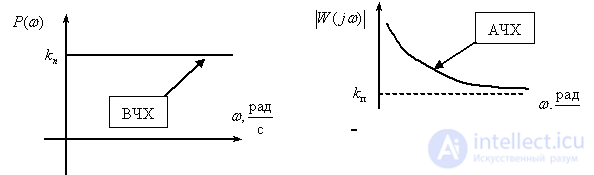
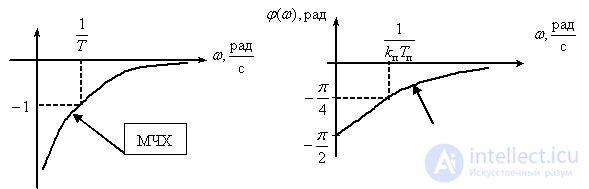
Frequency response
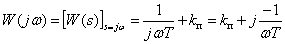 ,
,
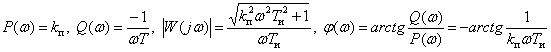 .
.

Test questions and tasks
Compare the characteristics of differentiating and really differentiating links. What do they have in common, and how do they differ?
Compare the characteristics of the integrator and integrator with a lag. What do they have in common, and how do they differ?
The differential equation describing the dynamic link has the form -
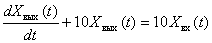 .
.
Determine the transfer function of a typical dynamic link and its name.
Answer :
We have aperiodic link with transfer function -
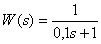 ,
,
The transfer function of the dynamic link has the form -
,
how to change the amplitude of the harmonic signal with frequency 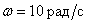 how many times?
how many times?
Answer :
The signal will decrease 10 times.
The transfer function of the dynamic link has the form -
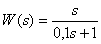 ,
,
how to change the phase of the harmonic signal with frequency 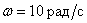 ?
?
Answer :
The output will be ahead of the input to 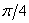 .
.
The transfer function of the dynamic link has the form -
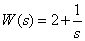 ,
,
Determine the angle of inclination of the transient characteristics of this link.
Answer :
Tilt angle is 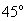 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control