Lecture
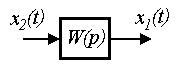
Elementary links are called the simplest components (blocks) of a system whose behavior is described by algebraic equations or differential equations of the 1st – 2nd order:
(2.50) 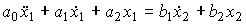 ,
,
Where 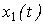 - output variable
- output variable 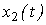 - input variable
- input variable 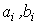 - constant coefficients (parameters). Equation (2.50) can be written in operator form:
- constant coefficients (parameters). Equation (2.50) can be written in operator form:
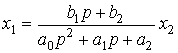 ,
,
those. the transfer function of the link is
(2.51) 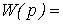
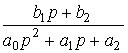 .
.
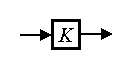
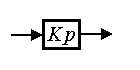
Proportional (inertia-free) link . The link is described by an algebraic equation.
(2.52) 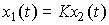 ,
,
Where 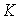 - coefficient of proportionality, which (due to the lack of inertial properties of the block) coincides with the static characteristic. Proportional transition function -
- coefficient of proportionality, which (due to the lack of inertial properties of the block) coincides with the static characteristic. Proportional transition function -
(2.53) 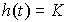 .
.
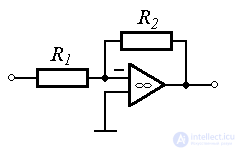
Examples: measuring potentiometers, gearboxes, voltage amplifiers ( 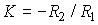 ) etc.
) etc.
Aperiodic link. The link is described by a differential equation
(2.54) 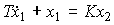
or, in reduced form, by the equation
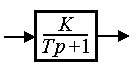
(2.55) 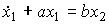 ,
,
Where 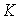 - coefficient,
- coefficient, 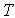 - time constant, a = K / T, b = 1 / K. The operator form of the link has the form
- time constant, a = K / T, b = 1 / K. The operator form of the link has the form
(2.56) 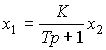
or accordingly
(2.57)  ,
,
The transition function of the link is determined by the expression
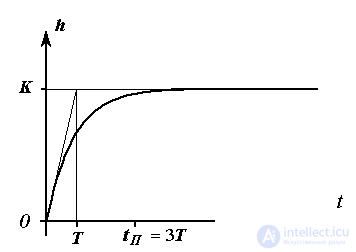
Fig. 2.10. Transition function aperiodic link
(2.58) 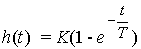 ,
,
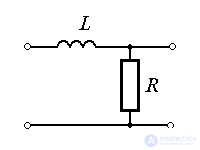
and the static characteristic is
(2.59) 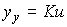 .
.
Examples: power amplifiers, thermal processes, engine acceleration process  - chain (see example 1.1), LR chain.
- chain (see example 1.1), LR chain.
Integrating link. The link is described by a differential equation
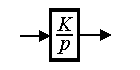
(2.60) 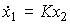
or, in operator form
(2.61) 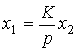 .
.
Transition function integrator
(2.62) 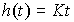 .
.
The link belongs to astatic blocks and therefore has no static characteristic.

Fig. 2.11. Transition function integrator
Examples: elements of mechanical systems (see the movement of a material point, example 2.3), described by the equations of the dynamics of a type
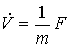 ,
,
and kinematic equations
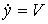 ;
;
electronic integrators ( 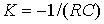 ) etc.
) etc.
Differentiating link (perfect). The link is described by a differential equation
(2.63) 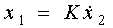
or, in operator form,
(2.64) 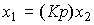 .
.
Differential Link Transition Function -
(2.65) 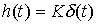 ,
,
and the response of the link to the linearly increasing signal x 2 = t -
(2.66) 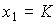 .
.
When x 2 = const for any t> 0 , 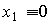 and, therefore, the static characteristic of the link is a direct
and, therefore, the static characteristic of the link is a direct 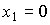 .
.
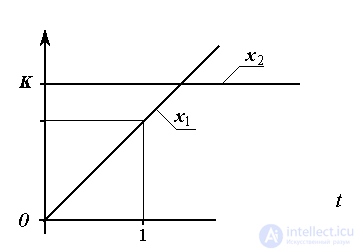
Fig. 2.12. Differentiator response  on linearly increasing impact
on linearly increasing impact 
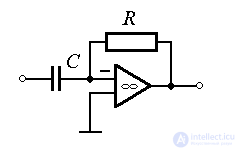
Examples: tachogenerator (electric speed sensor), electronic differentiator ( 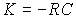 ).
).
Remark 2.4 . The output of the differentiating link is the derivative of the input signal, i.e. its instant speed is dx 2 / dt . The operation of finding the current value of the velocity x 1 (t) = dx 2 (t) / dt only from the information about the signal at the given time t currently x 2 (t) is not physically realizable and therefore there are no ideal differentiating links. However, the derivative can be approximated as 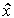 1 (t) = D x 2 (t) / D t , where D t is the time interval, D x 2 is the corresponding signal increment x 2 . By reducing the interval D t you can get the value
1 (t) = D x 2 (t) / D t , where D t is the time interval, D x 2 is the corresponding signal increment x 2 . By reducing the interval D t you can get the value 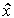 1 (t) , arbitrarily close to the current speed value x 1 (t) . Consequently, despite the unrealizability (with absolute precision) of the operation of differentiation, it is theoretically possible to build a link that ensures finding the derivative dx 2 (t) / dt with arbitrarily high accuracy.
1 (t) , arbitrarily close to the current speed value x 1 (t) . Consequently, despite the unrealizability (with absolute precision) of the operation of differentiation, it is theoretically possible to build a link that ensures finding the derivative dx 2 (t) / dt with arbitrarily high accuracy.
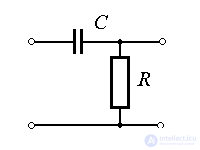
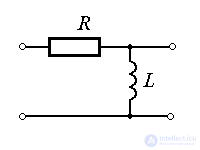
Real differentiating link. The link is described by the equation
(2.67) 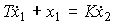 .
.
or, in operator form,
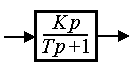
(2.68) 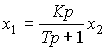
The transition function of the link is
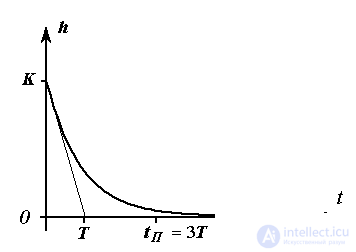
Fig. 2.13. Transition function of a real differentiator
(2.69) 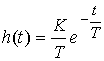 ,
,
and the response of the link to the linearly increasing signal x 1 = t coincides with the transition function of the aperiodic link, i.e.
(2.70) 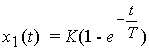 .
.
When x 2 = const and 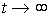 performed
performed 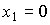 that corresponds to the static characteristic of the link.
that corresponds to the static characteristic of the link.
With sufficiently small time constants T , the characteristics of the link approach the characteristics of the ideal differentiating link (see Remark 2.4).
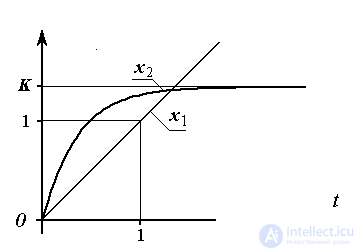
Fig. 2.14. Real Differential Link Reaction 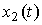 on linearly increasing impact
on linearly increasing impact 
Examples: CR and RL chains.
Oscillating link . The link is described by a 2nd order differential equation.
(2.71) 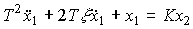 ,
,
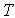 - time constant
- time constant 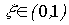 - attenuation parameter, or operator equation (2.50), where the transfer function is
- attenuation parameter, or operator equation (2.50), where the transfer function is
(2.72) 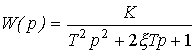 .
.
The roots of the characteristic equation take values
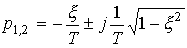
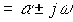 ,
,
Where 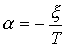 - attenuation coefficient,
- attenuation coefficient, 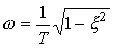 - The angular frequency of oscillation.
- The angular frequency of oscillation.
The transition function of the link is
(2.73) 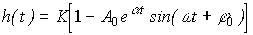 ,
,
Where 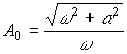 ;
; 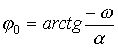 , and the static characteristic is
, and the static characteristic is
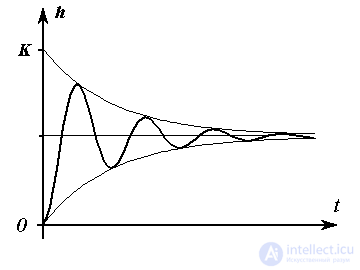
Fig. 2.15. Oscillating transition function
(2.74)  .
.
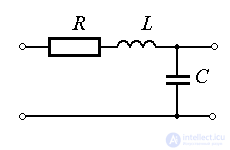
Examples: pendulum in a viscous medium, 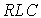 - chain.
- chain.
Remark 2.5. In the limiting case, 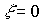 At the output of the link, continuous oscillations occur, and
At the output of the link, continuous oscillations occur, and 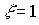 - monotonous (aperiodic) process, which corresponds to the conservative and double aperiodic link considered below.
- monotonous (aperiodic) process, which corresponds to the conservative and double aperiodic link considered below.
Conservative link (oscillator). The link is described by a differential equation
(2.75) 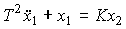
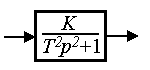
or operator equation (2.50), where
(2.76) 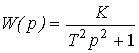 ,
,
and is obtained from the oscillatory level when 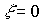 . Conservative link has pure imaginary poles.
. Conservative link has pure imaginary poles.
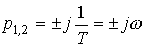
and transition function
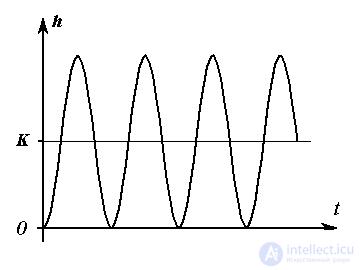
Fig. 2.16. Oscillating transition function
(2.77) 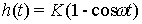 ,
,
Where 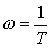 . The link has no static characteristic.
. The link has no static characteristic.
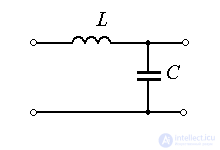
Examples: pendulum in vacuum; ideal oscillatory (LC) circuit.
Double aperiodic link. The link is described by the equation
(2.78) 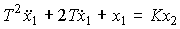
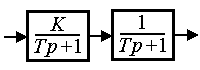
or operator equation (2.50), where
(2.79) 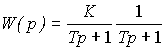 .
.
The link has equal real roots of the characteristic equation
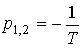 ,
,
and transient function
(2.80) 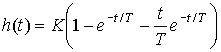 .
.
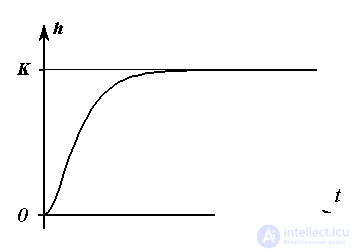
Fig. 2.17. Double aperiodic transition function
Static Link Characterization
(2.81) 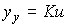 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control