Lecture
The quality of transients in systems and objects with harmonic effects is assessed by frequency characteristics, taken experimentally or calculated by the parameters of a mathematical model. In this case, receive frequency criteria for the quality of transients, which are classified as indirect criteria.
Frequency criteria are determined by one of the frequency characteristics: amplitude-phase, amplitude, real or logarithmic amplitude. Consider as a basis the definition of indirect indicators of quality on the amplitude frequency response (AFC) systems.
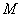 - an indicator of oscillation, defined as the ratio of the maximum value of the frequency response to its value at
- an indicator of oscillation, defined as the ratio of the maximum value of the frequency response to its value at 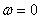
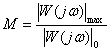

Fig. one
Vibration index characterizes the tendency of systems or objects to oscillation. The higher the oscillation index, the more oscillatory the system, i.e., lower quality.
With 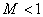 The transient response of the system is non-oscillatory, and the frequency response of the system has the approximate form shown in fig. 2
The transient response of the system is non-oscillatory, and the frequency response of the system has the approximate form shown in fig. 2

Fig. 2
If a 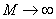 , then they speak of undamped oscillations of the transient response, and the frequency response of the system has the form shown in Fig. 3
, then they speak of undamped oscillations of the transient response, and the frequency response of the system has the form shown in Fig. 3

Fig. 3
Considered valid if 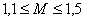 .
.
 - the resonant frequency of the system or object at which the frequency response has a maximum.
- the resonant frequency of the system or object at which the frequency response has a maximum.

With 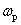 harmonic signals pass through the system with the highest gain.
harmonic signals pass through the system with the highest gain.
The control bandwidth is the frequency range from 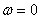 up to frequency
up to frequency 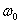 in which the condition is met
in which the condition is met
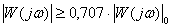 .
.

Fig. four
The bandwidth of the systems should not be very wide, so as not to pass high-frequency interference. On the other hand, the higher the frequency of signals transmitted by the system, the higher its speed. In electric drives, the passband is set in hertz, for motor speed control systems, the passband is, depending on the type of motor and energy converter, 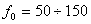 Hz
Hz
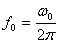 ,
,
this imposes an additional restriction on the fact that the phase-frequency characteristic in the passband should not fall below 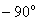 .
.
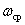 - cutoff frequency at which the frequency response of the system takes a value equal to one
- cutoff frequency at which the frequency response of the system takes a value equal to one
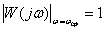 ,
,
as shown in fig. five.

Fig. five
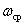 indirectly characterizes the duration of the transition process, as well as
indirectly characterizes the duration of the transition process, as well as 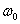 . System control time is inversely proportional to the cutoff frequency -
. System control time is inversely proportional to the cutoff frequency -
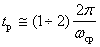 ,
,
if the transition process has 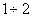 fluctuations, it is possible to establish a relationship between the cutoff frequency and the time to reach the first maximum
fluctuations, it is possible to establish a relationship between the cutoff frequency and the time to reach the first maximum
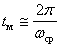 .
.
The cut-off band, as a characteristic of the speed of systems, has become widespread, since it is easily determined on logarithmic frequency characteristics (see Fig. 6).

Fig. 6
Integral quality assessment
Integral assessments of the quality of the transitional process of control systems are called time integrals of some functions of the transient process of changing the control error.
Consider the scalar linear system shown in Fig. 7. The system control input receives a step signal with amplitude 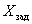 The system is designed to stabilize the setpoint of the controlled variable.
The system is designed to stabilize the setpoint of the controlled variable. 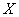 , scalar step perturbation can also act on the system
, scalar step perturbation can also act on the system 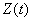 seeking to reduce the value of the controlled variable.
seeking to reduce the value of the controlled variable.

Fig. 7
Approximate view of graphs of transient processes of a controlled variable 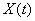 and regulation errors -
and regulation errors -
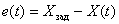 ,
,
shown in fig. 8 and 9.
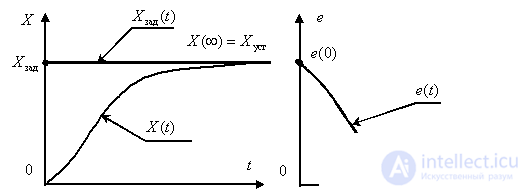
Fig. eight
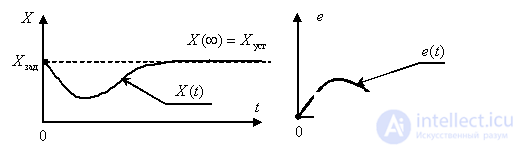
Fig. 9
The main areas of application of integral estimates in the theory of automatic control are:
The overall assessment of the attenuation rate and the deviation of the regulated value in the aggregate, without determining both of them separately.
The choice in the synthesis of system parameters that ensure the optimality of the transition process in terms of achieving a minimum of integral estimates.
The simplest integral estimate can be a linear integral estimate of the following form -
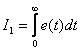 .
.
The geometric interpretation of this integral is the area under the curve. 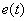 , as shown in Fig. 10 for transient changes in control and perturbation errors.
, as shown in Fig. 10 for transient changes in control and perturbation errors.
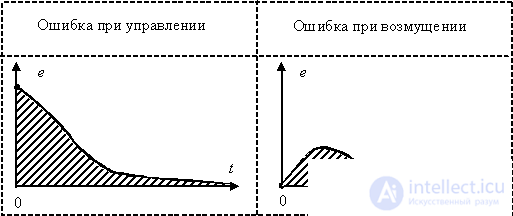
Fig. ten
If the control system is stable and has the property of astatism, then
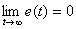 ,
,
and the integral 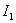 tends to a final value equal to the area under the curve
tends to a final value equal to the area under the curve 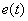 . Control system parameters tend to be chosen in such a way as to achieve a minimum
. Control system parameters tend to be chosen in such a way as to achieve a minimum 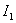 while the ideal transition process will strive for the perfect step form.
while the ideal transition process will strive for the perfect step form.
Test questions and tasks
How to determine the oscillation index of the frequency response of the system?
How to determine the cutoff frequency and bandwidth by frequency response?
How does the cut-off frequency of the system and its speed correlate?
Define a linear integral estimate, indicate its advantages and disadvantages.
Why for integral assessments of the transition process use the schedule of change of regulation error?
According to the frequency response of the system

Determine the vibrational index and cut-off frequency of the system.
Answer:
Vibrational index 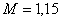 cutoff frequency
cutoff frequency 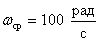 .
.
According to the graphs of the frequency response of two systems: SAU1 - 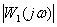 , SAU2 -
, SAU2 - 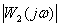 ,
,
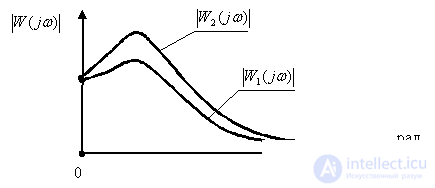
determine the control system, the transients of which have a large oscillation.
Answer:
The SAU2 system has a great oscillation of transients.
According to the graphs of the frequency response of two systems: SAU1 - 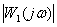 , SAU2 -
, SAU2 -  ,
,
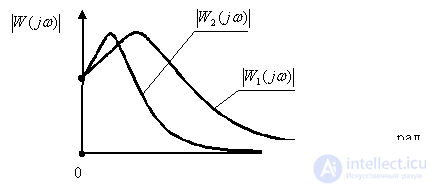
identify a control system that is faster.
Answer:
The SAU1 system has a great oscillation of transients.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control