Lecture
Aperiodic link
Transmission function -
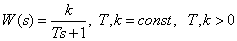 .
.
Frequency response -
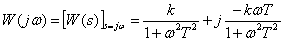 ,
,
Frequency response and phase response
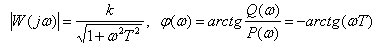 .
.
Logarithmic characteristics
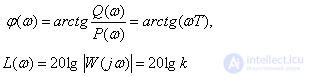
In this case, at the frequency -
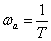
we have
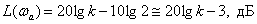 .
.
Consider two characteristic ranges for the aperiodic link:
| (one) |
| (2) |
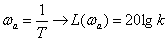 ,
,
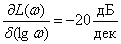 .
.
Expressions (1) and (2) are the equations of straight lines - asymptotes, to which LAFH aspire away from the point of their conjugation. 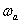 . As we will see later, in the synthesis and analysis of systems, it is more convenient to use not exact, but asymptotic characteristics.
. As we will see later, in the synthesis and analysis of systems, it is more convenient to use not exact, but asymptotic characteristics.

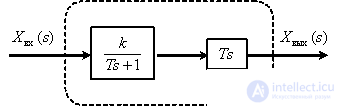
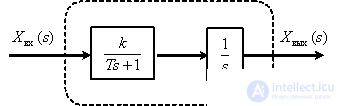
As we saw when working with the simplest typical links, frequency characteristics can be obtained from the transfer function. In more complex cases, when solving the problems of synthesis and analysis of the ACS, there is a need to obtain the characteristics of the ACS based on the known characteristics of the links included in the ACS.
The most frequently used case is when the links in the ACS are switched on sequentially, as shown in Fig. one.

Fig. one
In accordance with the rules of equivalent transformations, the transfer function of the entire ACS will have the form -
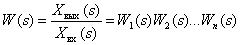 .
.
Get the frequency response of the ACS
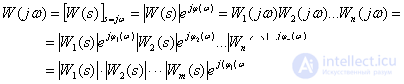
Consequently,
AChH SAU -
| (3) |
AFF SAU
| (four) |
We obtain, using expressions (3) and (4), the logarithmic characteristics of the ACS:
LAFH -
| (five) |
LFCH -
| (6) |
Thus, the logarithmic frequency characteristics of the ACS can be defined as the sum of the logarithmic frequency characteristics of the series-connected components of the ACS units. The logarithmic scale and the use of asymptotes allows summation graphically.
TAU also uses the properties of logarithmic frequency characteristics of dynamic links, the transfer functions of which are reciprocal -
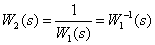 .
.
Let the frequency characteristics of the link 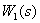 known:
known:
Frequency response -
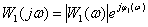 ,
,
LAFH -
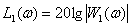 ,
,
LFCH -
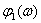 .
.
Then the frequency characteristics of the link 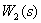 have the form:
have the form:
Frequency response -
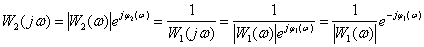 ,
,
LAFH -
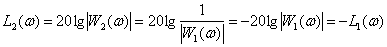 ,
,
LFCH -
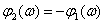 .
.
Thus, LAFH and LFCH of the inverse dynamic links are located symmetrically with respect to the frequency axis, which is confirmed by the previously obtained LAFH and LFCH of the differentiating and integrating links.
Example
For SAU was determined transfer function. LACHH SAU should be determined.
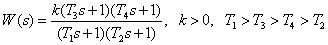 .
.
Decision
Imagine the ACS in the form of serially connected dynamic links.
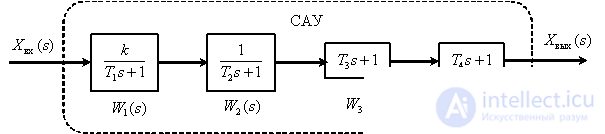
We obtain asymptotic LAFC for each aperiodic link
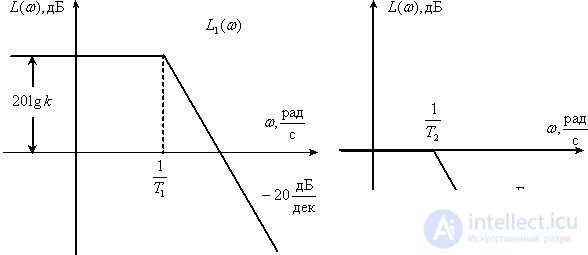
Using the properties of LAFC of reciprocal links, we obtain the asymptotic LPPH of forcing links 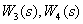 .
.

We obtain the asymptotic LAFC of SAU by performing the graphical summation of LAFC of links
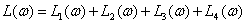 .
.
The task is greatly simplified by the fact that asymptotic graphs of links have sections with integer slope.

We obtain LAFC and LFCH typical units using the above.
Real differentiating link
Transmission function
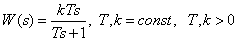 .
.
Imagine a link in the following form
Then LAFH and LFCHH have the form -
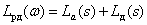 ,
,
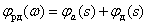 .
.

Integrating Link with Lag
Transmission function
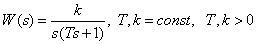 .
.
Imagine a link in the following form
Then LAFH and LFCHH have the form -
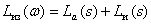 ,
,
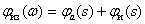 .
.

Proportional-integral link
Transmission function
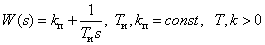 .
.
Imagine a link in the following form
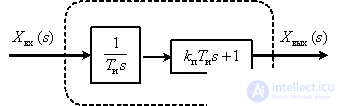
Then LAFH and LFCHH have the form -
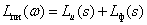 ,
,
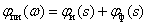 .
.

Test questions and tasks
How can be used to obtain the frequency characteristics of the system that the system can be represented in the form of parallel-connected typical dynamic links?
How do LAFC and LPCh of dynamic links, the transfer functions of which are reciprocal?
Which consecutively type dynamic links should be split into a really differentiating link to get its asymptotic LAFH and LFCH?
Which consecutively connected dynamic links should be broken into an integrating link with delay in order to get its asymptotic LAFH and LFCH?
Which serially-connected typical links should be split proportionally to the integrating link in order to get its asymptotic LAFC and LFCh?
Link Transfer Function -
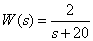 ,
,
At what frequency LFCHH will matter 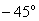 .
.
Answer :
At frequency 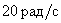 .
.
Link Transfer Function -
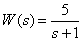 ,
,
As with frequency 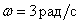 Will the exact and asymptolic LAFCH of this link differ?
Will the exact and asymptolic LAFCH of this link differ?
Answer :
Asymptotic LAFC will be less accurate on 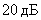 .
.
The transfer function of the object has the form -
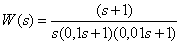 ,
,
Build an asymptotic LAFC object?
Answer :

Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control