Lecture
The disadvantage of the quadratic integral estimate 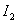 As with previous assessments, the fact that minimizing estimates does not impose restrictions on the form of the transition process. For example, shown in Fig. 1 graphics
As with previous assessments, the fact that minimizing estimates does not impose restrictions on the form of the transition process. For example, shown in Fig. 1 graphics 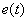 - (a, b, c) can have the same values
- (a, b, c) can have the same values 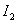 while significantly different in the form of the transition process.
while significantly different in the form of the transition process.

Fig. one
In addition, it often turns out that selected by 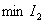 system parameters lead to a substantially oscillatory process, large derivatives due to the desire to bring the process closer to an ideal jump.
system parameters lead to a substantially oscillatory process, large derivatives due to the desire to bring the process closer to an ideal jump.
Therefore, another type of integral quadratic estimate is used, in which the restriction is imposed not only on the deviation 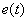 but also at the rate of its change
but also at the rate of its change 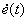 . This estimate has the following form -
. This estimate has the following form -
| (one) |
Where 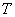 - some time constant.
- some time constant.
Difference between grades 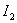 and
and 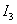 can be represented graphically, as shown in Fig. 2
can be represented graphically, as shown in Fig. 2

Fig. 2
That is optimized by 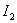 the transition process strives for a perfect leap, and optimized by
the transition process strives for a perfect leap, and optimized by 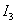 - to the curve of exponential type, which is described by the following expression -
- to the curve of exponential type, which is described by the following expression -
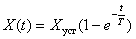 .
.
We prove the last statement. To do this, we analyze the expression (1).
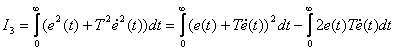 ,
,
given that
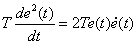 ,
,
we get
| (2) |
Given the fact that the last term in (2) is a constant value -
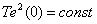 ,
,
square estimate 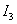 will have a minimum at
will have a minimum at
| (3) |
The solution of the differential equation (3) has the form -
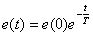 ,
,
and if we go from errors to output variables, we get -
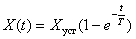 ,
,
Q.E.D.
Consequently, choosing system parameters by 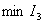 , you can bring the transition process to the exponent with a given time constant
, you can bring the transition process to the exponent with a given time constant 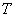 thus limiting the rate of increase of the output value
thus limiting the rate of increase of the output value  .
.
Method of determination 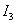 may be similar to the method of determining
may be similar to the method of determining 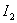 , considered above, if we present the quadratic estimate with the derivative in the following form -
, considered above, if we present the quadratic estimate with the derivative in the following form -
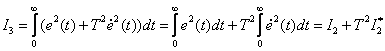 ,
,
Where  is determined by the formulas for
is determined by the formulas for 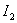 but considering the order of the numerator
but considering the order of the numerator 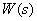 -
- 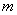 increases by 1.
increases by 1.
In the theory of automatic control, quadratic estimates with higher order derivatives are used (up to 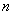 ) to more accurately specify the desired form of the transition process, it is natural that this also complicates the process of calculating estimates.
) to more accurately specify the desired form of the transition process, it is natural that this also complicates the process of calculating estimates.
Calculation of quadratic integral estimates
Consider the calculation and use of quadratic errors in an example.
Example
In a control system with a transfer function -
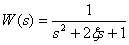 ,
,
let's set 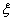 :
:
from the condition 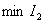 ,
,
from the condition 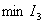 ,
,
and compare transients for these two cases.
Decision
Get the expression for 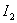 . To do this, convert the transfer function of the system to the specified form
. To do this, convert the transfer function of the system to the specified form
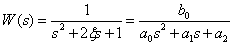 ,
,
then we get
| (four) |
Expression for 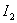 takes the form -
takes the form -
| (five) |
We define the components (5) according to the parameter of the transfer function of the system (4).
| (6) |
To find 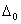 define (
define ( 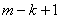 ), with
), with 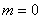 ,
, 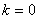
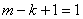 ,
,
Replace in the expression (6) for  first column view column
first column view column
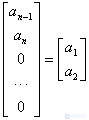 .
.
Then we get
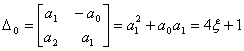 .
.
Define 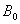 -
-
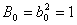 .
.
After substituting the obtained components into (5), we obtain the expression for the quadratic integral estimate.
| (five) |
Find the expression for the partial derivative with respect to 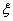 from the expression (5)
from the expression (5)
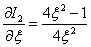 ,
,
equating the resulting expression to zero, we obtain the equation for finding the optimal value 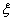 .
.
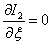 .
.
As a result, we obtain the value optimized by the quadratic estimate.  -
-
| (6) |
The transfer function of the system 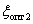 take the form -
take the form -
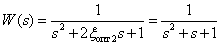 .
.
In fig. 3 we show the view of the transient process of the system with a single step effect and optimized by 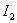 by parameter.
by parameter.

Fig. 3
Thus, we have the following indicators of the quality of the transition process,
| (7) |
Define 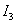 according to the method developed above for
according to the method developed above for 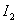 -
-
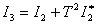 ,
,
expression for 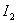 we take from the previous case -
we take from the previous case -
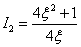 .
.
Define now 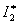 . The transfer function of the system for this case has the form -
. The transfer function of the system for this case has the form -
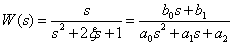 ,
,
then we get
| (eight) |
Expression for 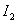 takes the form -
takes the form -
| (9) |
We define the components (9) according to the parameter of the transfer function of the system (8).
| (ten) |
Determine the coefficients 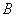 -
-
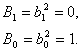 .
.
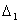 we do not define, because
we do not define, because 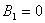 . To find
. To find 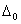 define (
define ( 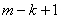 ), with
), with 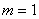 ,
, 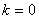
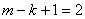 ,
,
Replace in expression (10) for  second column view column
second column view column
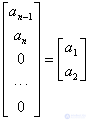 .
.
Then we get
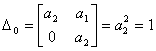 .
.
After substituting the obtained components into (9), we obtain the expression for the quadratic integral estimate.
| (eleven) |
Finally we get
| (12) |
Find the expression for the partial derivative with respect to 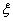 from expression (12)
from expression (12)
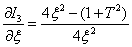 ,
,
equating the resulting expression to zero, we obtain the equation for finding the optimal value 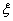 .
.
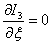 .
.
As a result, we obtain an optimized quadratic estimate with the derivative 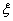 -
-
| (13) |
We believe for definiteness 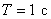 then
then
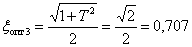 .
.
The transfer function of the system when 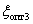 take the form -
take the form -
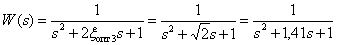 .
.
In fig. 3 we show the view of the transient process of the system with a single step effect and optimized by 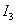 by parameter.
by parameter.

Fig. four
Thus, we have the following indicators of the quality of the transition process,
| (14) |
Comparing the transient processes, we see that when optimizing by a quadratic estimate taking into account the derivative ( 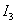 ) received significantly smaller values of overshoot and speed, with a smoother increase of the variable.
) received significantly smaller values of overshoot and speed, with a smoother increase of the variable.
Test questions and tasks
Give the definition of a quadratic integral estimate taking into account the derivative, explain its components.
What kind of transient process should we strive for while minimizing the integral quadratic estimate with regard to the derivative?
How to calculate the quadratic integral estimate taking into account the derivative?
Calculate the integral quadratic estimate of the transition process in the system with the transfer function -
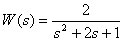 ,
,
if the input to the system is a single step function.
Answer :
Integral quadratic estimate 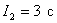 .
.
Calculate the integral quadratic taking into account the derivative estimate of the transition process in the system with the transfer function -
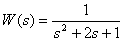 ,
,
if the input system is a single step function, and the time constant for the evaluation 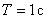 .
.
Answer :
Integral quadratic estimate 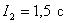 .
.
Determine the regulator parameter of the control system that provides the minimum of the quadratic estimate.
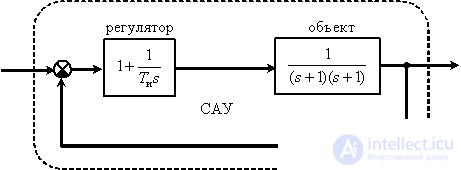
Answer :
Parameter proportional-integral controller 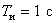
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control