Lecture
This group of criteria is based on an assessment of the quality of transients by the values of the poles and zeros of the transfer function of the system between the inputs and outputs of interest to us.
As is known, the transient response of a system can be defined as follows: -
| (one) |
Where 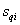 - the roots of the characteristic equation of the system
- the roots of the characteristic equation of the system
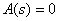 .
.
It is obvious that the character of the transition process is also affected by the numerator 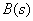 and denominator
and denominator 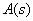 transfer function. But, in most cases, when analyzing systems by response to a control action,
transfer function. But, in most cases, when analyzing systems by response to a control action, 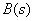 has no roots, that is, the transfer function has no zeros. Then the nature of the transition process can be assessed only by the poles of the transfer function, thereby exposing the analysis of the roots of the characteristic equation of the system -
has no roots, that is, the transfer function has no zeros. Then the nature of the transition process can be assessed only by the poles of the transfer function, thereby exposing the analysis of the roots of the characteristic equation of the system -
| (2) |
In the case of an approximate quality assessment based on the roots of the characteristic equation on the complex plane, the area of location of the roots is distinguished, the boundaries of which are set according to the quality requirements of the processes, as shown in Fig. one.

Fig. one
Borders of the area shown in fig. 1, are set by the following parameters:
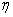 - criterion for the duration of the transition process,
- criterion for the duration of the transition process,
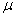 - oscillation of the transition process, is determined by
- oscillation of the transition process, is determined by  ,
,
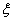 - maximum root removal from the imaginary axis.
- maximum root removal from the imaginary axis.
Consider these options.
Duration criterion 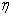 defined as the distance from the imaginary axis to the nearest real root or the nearest pair of complex conjugate roots.
defined as the distance from the imaginary axis to the nearest real root or the nearest pair of complex conjugate roots.
Find out whether this parameter characterizes the duration of the transition process? There are two cases of the location of the roots on the border area.
Let the closest to the imaginary axis, that is, lying on the border of the region, be the real root -
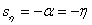 ,
,
then the corresponding component of the transition process, in accordance with (1) will be -
| (3) |
Where 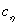 - decomposition coefficient (1).
- decomposition coefficient (1).
If the complex-conjugate pair of roots is closest to the imaginary axis,
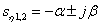 ,
,
then the corresponding component of the transition process, in accordance with (1) will be -
| (four) |
Where 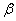 - oscillation frequency.
- oscillation frequency.
From (3) and (4) we see that the time attenuation components 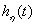 determines the factor -
determines the factor -
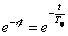 ,
,
Where 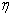 - the value of the minimum real root or minimum real part of the roots,
- the value of the minimum real root or minimum real part of the roots, 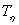 - corresponding
- corresponding 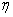 , the greatest time constant. Thus, we can assume that the transition process of the system is completed not earlier than the component
, the greatest time constant. Thus, we can assume that the transition process of the system is completed not earlier than the component 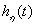 . Consequently,
. Consequently, 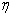 determines the duration of the transition process, being a quantity inversely proportional to the time of regulation. Knowing
determines the duration of the transition process, being a quantity inversely proportional to the time of regulation. Knowing 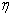 , we can estimate the time of regulation or transition process by the following relation -
, we can estimate the time of regulation or transition process by the following relation -
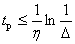 ,
,
Where  - half the width of the area, when hit in which the transition process is complete. If a
- half the width of the area, when hit in which the transition process is complete. If a 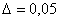 , and the extreme root is real, then we have -
, and the extreme root is real, then we have -
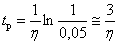 .
.
Oscillation criterion 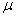 determined by angle
determined by angle 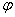 in the following way -
in the following way -
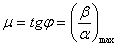 .
.
Where 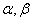 - respectively, the real and imaginary parts of the complex conjugate pair of roots located on the border of the region (see Fig. 1). By increasing
- respectively, the real and imaginary parts of the complex conjugate pair of roots located on the border of the region (see Fig. 1). By increasing 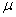 the oscillation of the system increases.
the oscillation of the system increases.
Farther from the imaginary axis, the boundary of the region 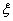 , determine the roots that have an extremely small impact on the transition process.
, determine the roots that have an extremely small impact on the transition process.
Other things being equal, the system requires an increase 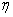 and declines
and declines 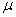 .
.
As an example of the influence of the location of the roots on the nature of the transient processes, we will show the graphs presented in Fig. 2 and 3.
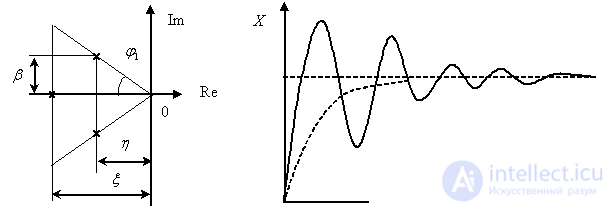 Fig. 2
Fig. 2
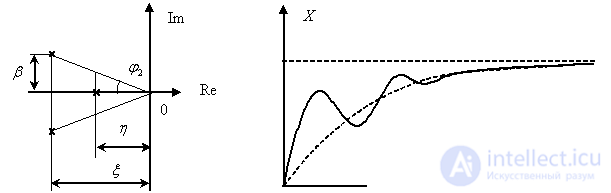 Fig. 3
Fig. 3
If the transfer function of the system has zeros, then the system quality assessment only by poles can give a significant error.
To clarify the nature of the influence of zeros on the quality of transient processes, let us present the system as follows, as shown in Fig. four.
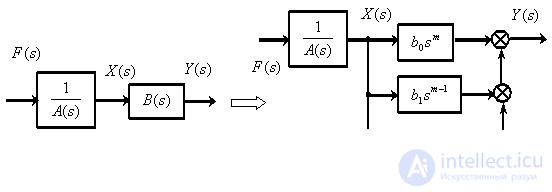
Fig. four
We specify the problem, let
 ,
,
but 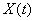 has the form shown in fig. 5. In this case, we consider two options for the schedule:
has the form shown in fig. 5. In this case, we consider two options for the schedule:
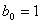 ,
,
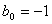 .
. From consideration of fig. 5 it can be concluded that members 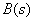 with positive coefficients lead to increased oscillation and speed, and negative coefficients delay the transition process.
with positive coefficients lead to increased oscillation and speed, and negative coefficients delay the transition process.

Fig. five
In those cases when it is required to obtain the desired type of transition process, methods are used based on the relationship of the coefficients of the characteristic equation of the system or its roots with the type of the transition process with given dynamic indicators.
Consider the characteristic equation of the form -
| (five) |
Convert (5)
| (6) |
According to the formula Vieta 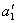 defined as the sum of all the roots of the equation,
defined as the sum of all the roots of the equation, 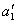 - the sum of the products of all pairs of roots,
- the sum of the products of all pairs of roots, 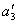 - the sum of the products of all triples of roots, etc., and
- the sum of the products of all triples of roots, etc., and 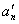 is defined as the product of all the roots of the equation -
is defined as the product of all the roots of the equation -
 .
.
Now, if we can specify the location of the roots on the complex plane, based on the requirements of the quality of the dynamics, then using the Vieta formulas, we can find the values of the coefficients of the characteristic equation that are related to the parameters of the system.
Pay special attention to the coefficient  the more
the more 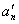 then, ceteris paribus, more real parts of the roots, therefore, faster transient. If the roots are real and multiple, then -
then, ceteris paribus, more real parts of the roots, therefore, faster transient. If the roots are real and multiple, then -
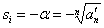 .
.
Denote
| (7) |
Where  is called the geometric mean root of the characteristic equation.
is called the geometric mean root of the characteristic equation.
Then equation (6) in view of (7) has the form -
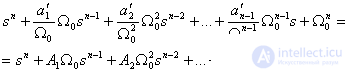
On the complex area of the roots of the characteristic equation 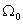 determines the point on the real axis - the geometric center of all the roots of the system, and the coefficients
determines the point on the real axis - the geometric center of all the roots of the system, and the coefficients 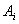 determine the relative position of the roots. It is easy to show that
determine the relative position of the roots. It is easy to show that 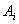 determine the transition curve in relative time
determine the transition curve in relative time 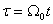 and value
and value 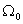 determines the time scale for this process.
determines the time scale for this process.
In practice, the above approach is used as follows:
For a particular system, determine the desired type of transition.
To ensure the specified requirements, the previously calculated coefficients of the characteristic equation are selected from the reference literature, thereby selecting the “desired” characteristic equation -
| (eight) |
Determine the characteristic equation for the structure and parameters of the system -
| (9) |
Where 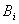 - coefficients functionally related to system parameters.
- coefficients functionally related to system parameters.
Get the system of algebraic equations, equating the coefficients of equations (8) and (9) with the same powers of the Laplace operator 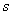 -
-
| (ten) |
The system (10) is solved with respect to the variable parameters of the system (parameters of the regulators), which makes it possible to determine the parameters providing the specified look and quality of the transition process.
The algorithm described above is often called the method of standard coefficients or the standard arrangement of the roots of the characteristic equation of the control system. Consider as an illustration two standard root arrangements that are most common in control systems for electromechanical drives of various installations.
Binomial root distribution
Binomial root distribution is used to ensure a given speed with the monotony of transients. The standard binomial characteristic equation has the form -
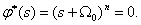
In this case, we have 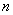 multiple real roots with a negative real part equal to
multiple real roots with a negative real part equal to 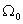 . View transients for
. View transients for 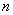 from 1 to 4 is shown in fig. 6. The characteristic equations for these cases are of the form -
from 1 to 4 is shown in fig. 6. The characteristic equations for these cases are of the form -
Butterworth distribution
Correct is the comparison of the automatic control system and the ideal low-pass filter (LPF), when for the system bandwidth (LF) a maximum horizontal position of LAFC is required, which ensures transmission of control signals without distortion. For the high frequency range (HF), they require maximum signal rejection, since this is a range of interference signals. Fig. 7 illustrates the approximation of the desired system characteristic to the characteristic of an “ideal” low-pass filter.
The distribution of Butterworth roots provides a compromise between these requirements, achieving a high uniformity in the LF passband with an acceptable slope of the characteristic in the HF suppression band.
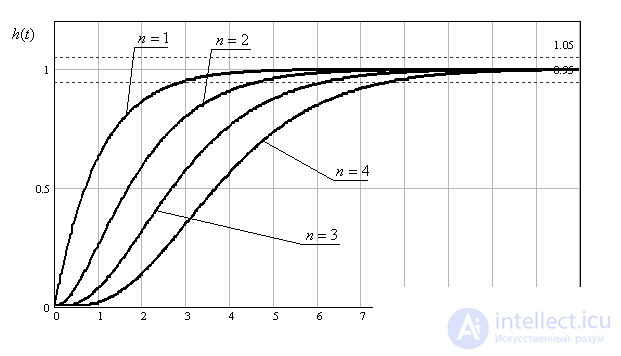
Fig. 6

Fig. 7
The roots of the characteristic equation are located on the complex plane, on a circle with a radius  and the angular distance between the roots -
and the angular distance between the roots - 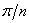 , symmetrically about the real axis, as shown in Fig. eight.
, symmetrically about the real axis, as shown in Fig. eight.
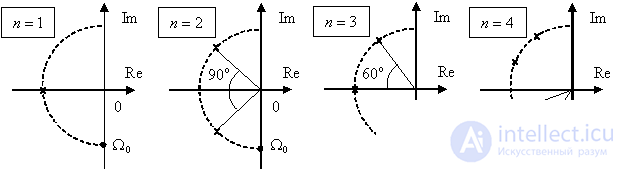
Fig. eight
View transients for 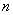 from 1 to 4 is shown in fig. 9.
from 1 to 4 is shown in fig. 9.
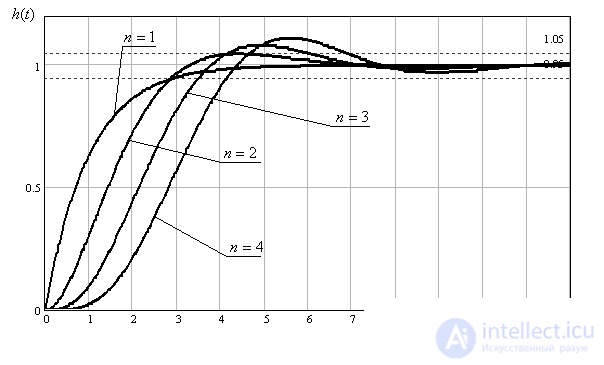
Fig. 9
The characteristic equations and parameters of the transition process for these cases have the form -
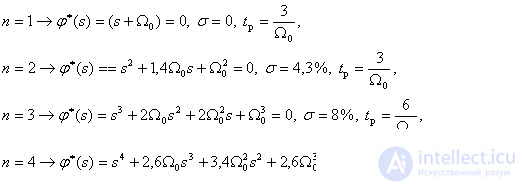
Comparison of transient characteristics shows that the Butterworth distribution provides a higher response than the binomial distribution, with low overshoot and oscillatory response.
Test questions and tasks
How to explain the effect on transient roots of the characteristic equation?
What component of the transition process gives the negative real root of the characteristic equation?
What components of the transition process give the complex conjugate roots of the characteristic equation?
What determines the roots of the characteristic equation closest to the imaginary axis of the complex plane?
How is the mean geometric root of the characteristic equation related to the system speed?
What effect does the transfer function zero have on the transient?
When should I use the binomial distribution of the roots of the characteristic equation for system settings?
When should I use the distribution of the roots of the characteristic Butterworth equation on the system settings?
Determine the coefficients of the characteristic equation with a binomial root distribution for a third-order control system, if the required regulation time 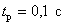 .
.
Answer :
The desired characteristic equation has the form -
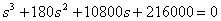 .
.
Determine the coefficients of the characteristic equation with the Butterworth root distribution for a fourth-order control system, if the required regulation time 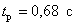 .
.
Answer :
The desired characteristic equation has the form -
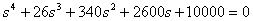 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control