Lecture
Identification of dynamic objects in the general case consists in determining their structure and parameters from the observed data - the input effects and output values.
In this case, the object (system element, control object, process element, etc.) is a black box. The researcher needs, subjecting the object to external influences and analyzing its reactions, to obtain a mathematical model (description of its structure and parameters), that is, to turn the “black box” into a “white box”, to achieve its “informational transparency”. Graphically, the identification process is illustrated in Fig. one.
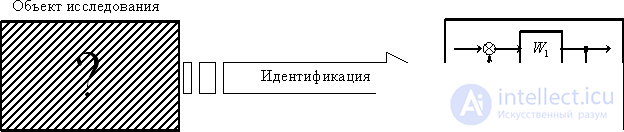
Fig. one
An important point of this process is the choice of points of application of external influences and the collection of information about the reactions of the object, that is, the placement of control devices and sensor systems.
It is solved when identifying objects and a simpler (relatively simple) task is the problem of identifying parameters when the structure of the mathematical model of the object is known in advance, but its parameters are not known. In this case, talking about the transition from the "gray box" to the "white box". Graphically, the process of identifying parameters is illustrated in Fig. 2

Fig. 2
The task of identifying parameters can either be a component of the general task of identifying an object, or be solved independently.
Consider on the generalized structure and procedure of the identification process, the basis of the approach to solving identification problems. The generalized structure of the identification process is shown in Fig. 3
Generalized identification procedure
Object classification.
The choice for a particular object class is a custom model, that is, the model, structure and parameters of which can be changed during the identification process.
Select the criterion (assessment) of the quality of identification, which characterizes the difference between the model and the object as a functional available for observation variables.
Choose an identification algorithm (model setting mechanism) ensuring the convergence of the identification process, minimum identification criteria.

Fig. 3
Identification methods can be divided into two groups:
active identification - identification outside the control loop,
passive identification - identification in the control loop.
Active Identification
In this case, the object of study is derived from the conditions of a normal environment (normal mode of operation, nominal parameters of the operating mode, etc.). Researches are conducted in specialized laboratory conditions, as shown in fig. 4. At the inputs of the object (working and additional) test signals of a special type are supplied. It can be:
step and pulse time signals,
harmonic signals,
random effects with given parameters.
Active identification is used in the development of new technologies in relation to existing industrial facilities, in the study of new phenomena, in the initial development of a mathematical model.
Passive identification
With passive identification, the object functions in the control loop, is in the process of normal operation. Its inputs receive only natural control signals.
Passive identification is used to refine the mathematical model, to track changes in the object. Information is operatively used in the object management system, the process of such identification is illustrated in Fig. five.
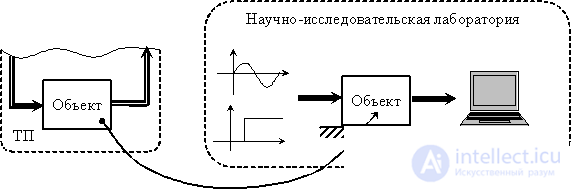
Fig. four

Fig. five
In addition to the listed groups of methods, mixed identification systems are also implemented, when the object is not removed from normal operation, but test actions are added to the control signals to identify the object without degrading the quality of the main control process.
Consider active identification in more detail.
Active identification of control objects can be performed both in the time domain and in the frequency domain. In this area, each area uses its own algorithms and identification methods.
With active identification, in most cases, the characteristics obtained as a result of experiments are used:
frequency characteristics (AFCh, LAFH, LFCHH, etc.),
temporal characteristics (step change of the task, "narrow" impulse of the task, etc.).
Consider as an example one of the approaches to the problem of identifying the structure and parameters of an object in the frequency domain. We restrict consideration to an object with one input and one output.
We know that if there is a mathematical model of such an object in the form of a transfer function -
| (one) |
then this corresponds to the availability of complete information about the structure and parameters of the object, all its characteristics.
We transform the transfer function (1) to the pole-zero representation, the Bode form -
| (2) |
Where 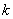 - gain (
- gain ( 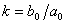 ),
), 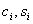 - respectively, the poles and zeros of the transfer function.
- respectively, the poles and zeros of the transfer function.
If among the roots ( 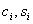 ) there are complex conjugate pairs of roots, then the expansion (2) must be supplemented with factors of the following type -
) there are complex conjugate pairs of roots, then the expansion (2) must be supplemented with factors of the following type -
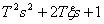 .
.
Assuming for simplicity, the absence of complex conjugate roots, we can convert (2) to the following form -
| (3) |
Where
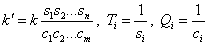 .
.
According to the expression for the transfer function in the form (3) we obtain the frequency response of the object -
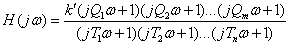 ,
,
LAFH -
| (four) |
LFCH -
| (five) |
On the other hand, we know that LAFH and LFCH of dynamic links with transfer functions are
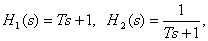
has the form shown in fig. 6, since the links are, respectively, forcing and aperiodic dynamic links of the first order.

Fig. 6
Based on the material presented, the following procedure can be proposed for the active identification of the structure and parameters of a linear system with one input and one output:
In the course of the experiment, the frequency response in the form of LAFC and LFCH is taken from the object.
The experimentally obtained LAFC is approximated by a piecewise linear curve 1 - a set of segments (asymptotes) with integer slope multiple  .
.
The slope of the asymptotes and the conjugation frequencies of the asymptotes determine the transfer function of the object as a product of the transfer functions of the corresponding asymptotes of the elementary dynamic links (aperiodic and forcing).
In the presence in the obtained LAFH and LFCHH signs of links of the second order, that is, the asymptotes with a multiple slope  , you must enter such links in the model.
, you must enter such links in the model.
Oscillating link with transfer function -
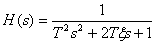 ,
,
has LAFH and LFCHH, shown in Fig. 7

Fig. 7
Secondary boost link with transfer function
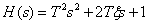 ,
,
has LAFH (LFCH) symmetric shown in Fig. 7 characteristics of the oscillating level relative to the frequency axis.
Consider an example of identification by the procedure described.
Example
By experimentally obtained LAFC object to determine the transfer function.
Decision
We approximate an experimental LAFH with a set of asymptotes, as shown in Fig. eight.
Consider now the areas of approximated LAFH, on which the slope does not change:
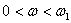 .
.
On this interval, the asymptote view corresponds to the LAFC of the integrator, its transfer function is
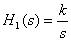 .
.
This link corresponds to the following expression LAFC -
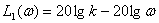 .
.
Use the last expression to define 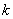 by substituting the characteristic value at frequency
by substituting the characteristic value at frequency 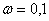
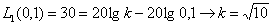 .
.

Fig. eight
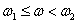 .
.
On this interval, the slope of the asymptote increased by 20 dB / dec, which corresponds to the addition of a first-order aperiodic link with the transfer function -
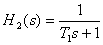 ,
,
where the time constant is determined by the conjugation point asymptotes -
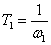 .
.
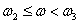 .
.
On this interval, the slope of the asymptote decreased by 20 dB / dec, which corresponds to the addition of a first-order forcing element with a transfer function -
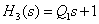 ,
,
where the time constant is determined by the conjugation point asymptotes -
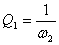 .
.
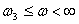 .
.
On this interval, the slope of the asymptote increased by 20 dB / dec, which corresponds to the addition of a first-order aperiodic link with the transfer function -
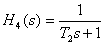 ,
,
where the time constant is determined by the conjugation point asymptotes -
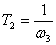 .
.
Multiplying the transfer functions obtained, we obtain the transfer function of the object -
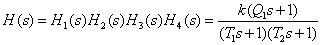 .
.
Test questions and tasks
Define the process of identifying an object, identifying parameters.
What methods are classified as passive identification methods?
What methods refer to active identification methods?
Explain the procedure for identifying the parameters of the control object by its experimental LAFC.
The asymptotic LAFC of the object has the form -

Determine the transfer function of the object.
Answer :
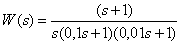 .
.
The asymptotic LAFC of the object has the form -

Determine the transfer function of the object.
Answer :
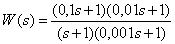 .
.
The asymptotic and exact LAFC of a dynamic link has the form -

Determine the transfer function of the link.
Answer :
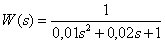 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control