You get a bonus - 1 coin for daily activity. Now you have 1 coin

Introduction Fractional rational and impulse functions.

Lecture



The purpose of teaching the discipline is to give students a fairly complete picture of the basic concepts and principles of obtaining, transforming and analyzing various types of mathematical models used in the theory of automatic control to describe control objects of various nature and control systems of various classes. In addition, students should master the skills of solving practical problems related to mathematical modeling in the theory of automatic control, rationally using the mathematical apparatus.

A wide range of methods for analyzing and synthesizing automatic control systems, various forms of representing mathematical models of objects of different nature used by specialists and bachelors requires the following tasks within the framework of the Mathematical Foundations of Automatic Control Theory (MOTAU) discipline:

  • the deepening of knowledge and the formalization of representations in the field of the foundations of the mathematical description of automatic control systems, such sections of higher mathematics as fractional rational functions of a complex variable, impulse functions, Fourier and Laplace transforms, an operator method for solving differential equations, linear algebra;

  • the formation of knowledge and practical skills of obtaining and transforming various forms of mathematical models of dynamic units and automatic control systems in order to use them rationally in solving problems of analysis and synthesis of control systems;

  • studying the specifics of the methods of obtaining and transforming mathematical models of multidimensional control objects based on the apparatus of linear algebra and the representation of objects in the state space;

  • the study of methods for assessing the quality of processes in automatic control systems, the formation of practical skills in the use of various quality criteria for transients in the analysis and synthesis of automatic control systems;

  • the formation of concepts and practical skills in solving problems of the identification of elements of ACS.

The study of the discipline is based on the fact that the student has relevant mathematical training in the field of differential and integral calculi, linear algebra, complex numbers and trigonometric functions, as well as is familiar with the basic concepts and laws discussed in the courses of theoretical fundamentals of electrical engineering and theoretical mechanics. Education in the 4th semester takes place in parallel with the study of TOE (part 2), in the 5th semester - with the study of TAU (part 1).

The discipline is designed to study during the 4th and 5th semesters (2nd and 3rd year), includes 42 lecture hours, 28 hours of practical training and 14 hours of laboratory practical work (in the 5th semester).

The discipline includes the following main sections:

  • basics of mathematical description of automatic control systems,

  • types of mathematical models of dynamic links,

  • mathematical models of elementary dynamic links,

  • mathematical models of ACS,

  • features of mathematical models of multidimensional automatic control systems,

  • methods for assessing the quality of automatic control systems,

  • identification of the parameters of the mathematical model of automatic control systems.

Fractional Rational Functions

Fractional rational functions of a complex variable in various forms are widely used in TAU for representing transfer functions and solving problems of synthesis and analysis of ACS.

Fractional rational function of some real or complex variable 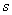Introduction Fractional rational and impulse functions. has the following form:

Introduction Fractional rational and impulse functions.

(one)

Where 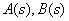Introduction Fractional rational and impulse functions. - polynomials of the numerator and denominator, 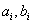Introduction Fractional rational and impulse functions. - real numbers 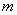Introduction Fractional rational and impulse functions. - the order of the numerator, 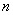Introduction Fractional rational and impulse functions. - the order of the denominator (the entire fractional rational function of the function), 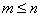Introduction Fractional rational and impulse functions. - for functions used in TAU.

Polynomials of a fractionally rational function can be represented as a product of binomials (decomposition of a polynomial into factors), then the function can be represented in the form of a Bode

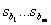Introduction Fractional rational and impulse functions.

(2)

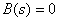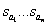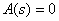Where Introduction Fractional rational and impulse functions. - roots of the equation Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. - the roots of the characteristic equation Introduction Fractional rational and impulse functions. .

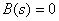Roots of the equation Introduction Fractional rational and impulse functions. called zero fractional rational functions Introduction Fractional rational and impulse functions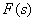. , because

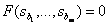Introduction Fractional rational and impulse functions. .

Roots of the characteristic equation 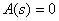Introduction Fractional rational and impulse functions. called poles of a fractional rational function, since

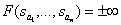Introduction Fractional rational and impulse functions. .

The poles and zeros can be real and complex conjugate numbers. Thus, the task of representing a function in the form of a Bode reduces to finding the roots of equations formed by the polynomials of the numerator and the denominator.

They are usually located on the plane of the complex variable. 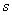Introduction Fractional rational and impulse functions. , marking the location of the poles with crosses, and zeros as circles. For a better mastery of this material, it is necessary to refresh in mind the information from higher mathematics on operations with complex numbers. Zeros, and especially the poles of fractional rational functions, are depicted on the plane of the complex variable 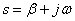Introduction Fractional rational and impulse functions. . In fig. 1 shows the location of the poles and zeros of some fractional rational function.

Introduction Fractional rational and impulse functions.

Fig. one

Imaginary axis divides the plane Introduction Fractional rational and impulse functions. on the right and left half-planes. Zeros and poles located in the right half-plane are called right, in the left half-plane - left. Complex poles and zeros are always arranged in pairs symmetrically with respect to the real axis; such pairs of roots are called complex conjugate roots. If among the zeros and poles there are two or more of the same, they are called multiples, unlike the others, which are called simple. The multiplicity is determined by the number of identical zeros or poles ( Introduction Fractional rational and impulse functions. - 2). Consider an example of getting a Bode form.

Example

Introduce the fractional rational function

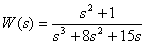
Introduction Fractional rational and impulse functions.

in the form of a Bode and show the location of the poles and zeros of the fractionally rational function on the complex plane.

Decision

Find the roots of the equation

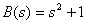Introduction Fractional rational and impulse functions. .

We get two complex conjugate roots (zero)

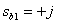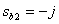Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. .

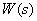
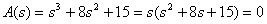Find the poles Introduction Fractional rational and impulse functions.

Introduction Fractional rational and impulse functions. .

We get three poles

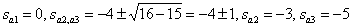Introduction Fractional rational and impulse functions. .

We show the location of the zeros and poles on the complex plane (see Fig. 2).

Introduction Fractional rational and impulse functions.

Fig. 2

The fractional rational function (1) is often represented as the sum of the simplest fractions (Heavisite form)

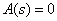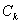Introduction Fractional rational and impulse functions.

(3)

Where Introduction Fractional rational and impulse functions. - the roots of the characteristic equation Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. - decomposition coefficients, which are found by the following function:

Introduction Fractional rational and impulse functions.

(four)

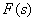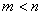Such a representation of a fractional rational function is possible if the poles Introduction Fractional rational and impulse functions. - simple as well Introduction Fractional rational and impulse functions. .

A function that has one zero pole can be represented as follows:

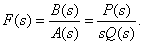
Introduction Fractional rational and impulse functions.

In this case, instead of formulas (3), (4) apply the expression

Introduction Fractional rational and impulse functions.

(five)

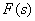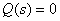Where Introduction Fractional rational and impulse functions. - nonzero poles Introduction Fractional rational and impulse functions. the roots of the equation Introduction Fractional rational and impulse functions. ,

Introduction Fractional rational and impulse functions.

(6)

Consequently, the representation of a fractional rational function in the form of Heavisite is reduced to finding the poles of a fractional rational function and the rational use of decomposition formulas. Consider a number of examples of obtaining the Bode form

Example

Introduce the fractional rational function

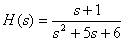
Introduction Fractional rational and impulse functions.

in the form of Hevisite, using the decomposition formulas (3), (4).

Decision

The numerator polynomial equation has the form

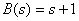Introduction Fractional rational and impulse functions. .

The characteristic equation is

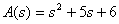Introduction Fractional rational and impulse functions. .

Find the roots of the characteristic equation

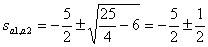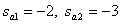Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. .

Define the derivative of the denominator polynomial

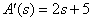Introduction Fractional rational and impulse functions. .

Determine the coefficients of the decomposition corresponding to the number of poles

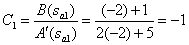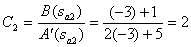Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. .

Then the Heavisite form is

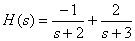Introduction Fractional rational and impulse functions. .

Example

Introduce the fractional rational function

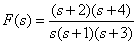
Introduction Fractional rational and impulse functions.

in the form of Hevisite, using the decomposition formulas (5), (6).

Decision

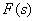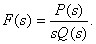
Imagine Introduction Fractional rational and impulse functions. as

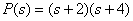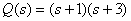Introduction Fractional rational and impulse functions.

Then

Introduction Fractional rational and impulse functions. ,

Introduction Fractional rational and impulse functions. .

Non-zero poles have the form

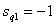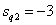Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. .

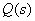
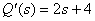Derivative of Introduction Fractional rational and impulse functions.

Introduction Fractional rational and impulse functions. .

Determine the coefficients of decomposition

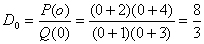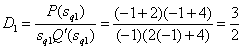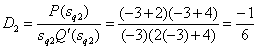Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. , Introduction Fractional rational and impulse functions. .

Then the Heavisite form is

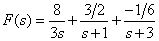Introduction Fractional rational and impulse functions. .

Impulse functions

Real signals (variables and influences) encountered in control systems are usually represented with the help of some idealizations — impulse functions. The most commonly used is the step unit function (Heavisite function) and the delta function (Dirac function), which are described as follows:

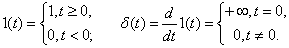
Introduction Fractional rational and impulse functions.

Graphs of these functions are shown in Fig. 3

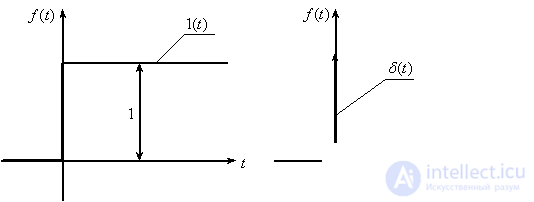
Introduction Fractional rational and impulse functions.

Fig. 3

For single and delta functions true

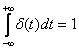Introduction Fractional rational and impulse functions. .

Thus, the delta function is an instantaneous pulse equal to infinity at zero time and zero at other times, the area of ​​which is constant and equal to one. Therefore sometimes Introduction Fractional rational and impulse functions. called a single impulse.

Test questions and tasks

    1. How to determine the order of fractional rational functions?

    2. Explain the procedure for converting a function to a Bode form.

    3. What poles of the fractional rational function are called simple?

    4. What is the idealization of the representation of a real signal by a single step function?

    5. Introduce the fractional rational function

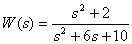
Introduction Fractional rational and impulse functions.

in the form of a bode.

Answer :

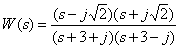Introduction Fractional rational and impulse functions. .

    1. Introduce the fractional rational function

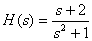
Introduction Fractional rational and impulse functions.

in the form of Hevisite.

Answer :

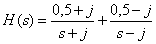Introduction Fractional rational and impulse functions. .

    1. Introduce the fractional rational function

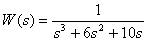
Introduction Fractional rational and impulse functions.

in the form of Hevisite.

Answer :

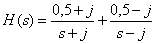Introduction Fractional rational and impulse functions. .

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Mathematical foundations of the theory of automatic control

Terms: Mathematical foundations of the theory of automatic control