Lecture
When considering and comparing the frequency characteristics of amplitude and phase-frequency for devices of various types, the problem of their compact representation arises, since the values of amplitudes and frequencies (see Fig. 1) differ significantly from each other. In addition, the value of the frequency range itself, in which the characteristics of a particular device are of interest, can be quite significant, from fractions of a hertz to tens of megahertz.
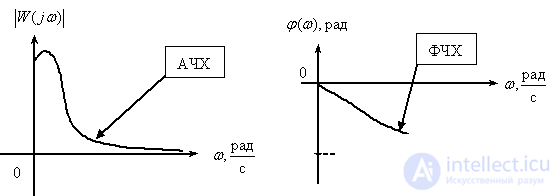
Fig. one
The solution to this problem lies in the use of logarithmic scales in frequency characteristics.
For the first time, they turned to logarithmic scales in communication technology, since they consider objects, both with large gain factors, and objects, which are characterized by a significant attenuation of signals.
The communication technique uses the concept of power transmission coefficient for a four-port network shown in fig. 2,

Fig. 2
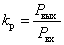 .
.
A significant range of variation of this coefficient and forced to use the logarithmic representation, the logarithmic transfer coefficient for power -
| (one) |
The logarithmic gain in power is measured by special units, which are called Bell (B).
1 Bell corresponds to a power increase of 10 times.
The most commonly used unit is ten times smaller - decibels (dB).
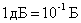 .
.
When determining the logarithmic coefficient in decibels, the expression (1) takes the form -
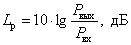 .
.
The logarithmic gain can be expressed in terms of the ratio of the output and input voltages with the same load resistances 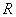
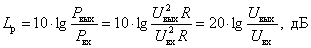 .
.
This representation of the gain is used in the theory of automatic control to measure the amplitude of the frequency response in decibels -
| (2) |
The frequency axis in the theory of automatic control also uses a logarithmic scale based on the decimal logarithm of frequency.
In this case, the frequency axis will have the following form -
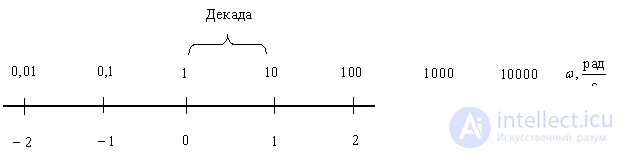
Fig. 3
The frequency change is ten times called decade. Moreover, on the frequency axis, at its logarithmic scale, it is customary to denote frequency values in rad / s, sometimes in hertz, this is especially accepted in radio engineering and in engineering practice.
We especially note that the logarithmic scale does not have a zero and can intersect the vertical axis in any place, which is especially important in that it makes it possible to consider the frequency properties of dynamic links and specific devices in the required frequency range, where the characteristic is of interest to the researcher.
Now we give the definition of logarithmic frequency characteristics.
The logarithmic amplitude frequency response (LAFC) of a dynamic link refers to such a representation of the amplitude frequency response (AFC), in which the modulus (amplitude) of the frequency response is expressed in decibels, and the frequency on a logarithmic scale.
The logarithmic phase frequency response (LPCh) of a dynamic link is called such a representation of the phase frequency response (PFC), in which the frequency is expressed on a logarithmic scale.
Quite often, LAFC and LPCHH are built on the same graph in order to give a complete picture of the properties of an object, we will show in Fig. 4 approximate appearance and design LAFH and LFCHH some inertial object.

Logarithmic frequency characteristics of elementary dynamic links
Instant link
Transmission function -
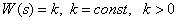 .
.
Frequency response -
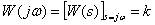 ,
,
Frequency response and phase response
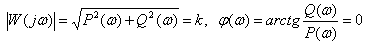 .
.
Logarithmic characteristics
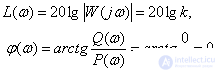

Differentiator link
Transmission function -
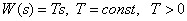 .
.
Frequency response -
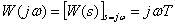 ,
,
Frequency response and phase response
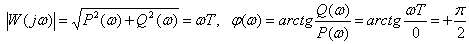 .
.
Logarithmic characteristics
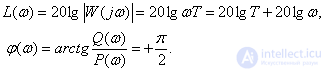
For convenience of construction, we define the point where LAFC intersects the frequency axis -
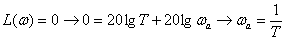 .
.
Determine the slope LAFC
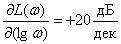 ,
,
that is, we obtain that LAFC receives an increment of 20 dB over the frequency range of 1 decade.

Integrating link
Transmission function -
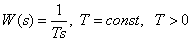 .
.
Frequency response -
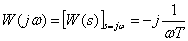 ,
,
Frequency response and phase response
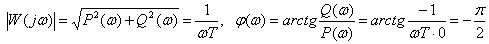 .
.
Logarithmic characteristics
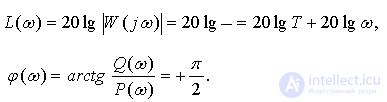
For convenience of construction, we define the point where LAFC intersects the frequency axis -
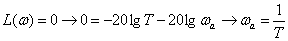 .
.
Determine the slope LAFC
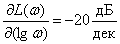 ,
,
that is, we obtain that LAFC receives a decrease of 20 decibels over the frequency range of 1 decade.

Test questions and tasks
Give a definition of 1 Bell.
How is the log power gain calculated for quadrupoles?
What defines the concept of "decade" in relation to logarithmic frequency characteristics?
Give a definition of the logarithmic amplitude frequency response.
Give a definition of the logarithmic amplitude frequency response.
List the main advantages of logarithmic frequency characteristics in comparison with usual frequency characteristics.
Link Transfer Function -
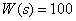 ,
,
How does it depend on the frequency LACH of this link? Determine the LAFC of this link.
Answer :
LAFH does not depend on the frequency
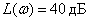 .
.
Link Transfer Function -
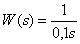 ,
,
Determine the value LAFC of this link at a frequency 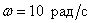 .
.
Answer :
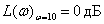 .
.
Link Transfer Function -
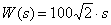 ,
,
Determine the slope LAFC of this link.
Answer :
The slope of LAFC of this link is 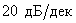 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control