Lecture
Above two types of models of a multidimensional system were considered. We establish a connection between these two species. Since the initial basis for mathematical models are differential equations, it will be logical to determine the relationship between the equations of state and the transfer matrices of the ACS. For this we apply the Laplace transform to the equations of state and output
| (one) |
| (2) |
at zero initial conditions, replace the originals of variables with Laplace images and obtain a system of vector-matrix operator equations
| (3) |
We define the relationship between the input vector and the state and output vectors. From the first equation of system (3) we have -
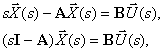
and if the matrix 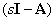 not degenerate, that is
not degenerate, that is 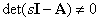 , we get -
, we get -
| (four) |
Where it follows that
| (five) |
Substituting (4) into (3), we get -
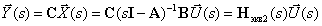 ,
,
The result is -
| (6) |
Recall that the components of equivalent matrices are the transfer functions of the system. Consequently, expressions (5) and (6) are universal formulas for calculating all the transfer functions of a multidimensional system required for the analysis, from which structural diagrams and frequency characteristics can be obtained.
Note that each element of equivalent matrices (transfer functions) has, by definition, an inverse matrix, a factor
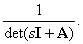
That is polynomial 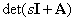 is the common denominator for all transfer functions, and the equation is
is the common denominator for all transfer functions, and the equation is
| (7) |
is the characteristic equation of the system.
Thus, we not only obtained a connection between mathematical models in the time and frequency domains, but also universal expressions for determining the transfer functions and the characteristic equations of any linear objects or control systems. The initial parameters for expressions (5), (6) and (7) are matrices of parameters of equations of state and output. You can perform transformations (5), (6) and (7) using a computer that has symbolic math programs, for example, such as Mathematica 3.0 (4.0), developed by Wolfram Research. in systems of the second and third order, these transformations can be performed manually.
Consider a few examples of obtaining and converting models.
Example
Consider an object, a circuit diagram of which is shown in Fig. one.

Fig. one
Perform the following tasks for this object:
Get the equation of state.
Determine the characteristic equation of the object.
Determine the transfer matrix object.
Getting the equation of state
We write the differential equations describing the processes in the scheme
| (eight) |
Set the state and input vectors:
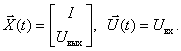
We get that  . We write the equation of state in expanded form for our case:
. We write the equation of state in expanded form for our case:
| (9) |
Let us open matrix brackets in (9):
| (ten) |
Let us bring the system of equations (8) to the form (10), using zero coefficients in the absence of a variable in the right-hand sides:
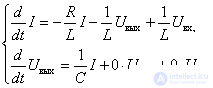
All components of the parameter matrices are now known, and the equation of state can be written
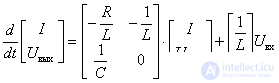 .
.
Therefore, the parameter matrices have the following form -
| (eleven) |
The definition of the characteristic equation of the object
The characteristic equation of the system is determined by the matrices of parameters of the equation of state (11), using the expression (7) -
| (12) |
Substituting in (12) the expression for the matrix of parameters 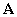 and the unit matrix
and the unit matrix  , we obtain the characteristic equation
, we obtain the characteristic equation
| (13) |
The definition of the transfer matrix of the object
We define the equivalent transfer function matrix, which connects the state and control vectors by expression (5), which in our case is:
| (14) |
Matrix 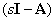 can be determined from (13)
can be determined from (13)
 .
.
We define the inverse matrix, remembering 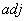 - an adjunct of the original matrix is a transposed matrix of algebraic complements of the matrix elements, and algebraic additions are determined for each element of the original matrix by the following expression -
- an adjunct of the original matrix is a transposed matrix of algebraic complements of the matrix elements, and algebraic additions are determined for each element of the original matrix by the following expression -
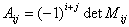 ,
,
Where 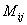 - the minor of the initial matrix, obtained by crossing out
- the minor of the initial matrix, obtained by crossing out 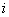 - oh line and
- oh line and 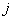 th column.
th column.
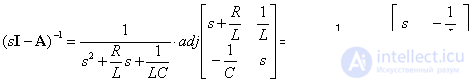 .
.
Finally we get -

Consequently, we obtain the transfer functions of the object.
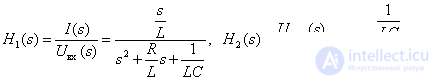 .
.
Example
DC motor of independent excitation (with permanent magnets) as a control object is described by the following system of differential equations -
| (15) |
Where 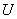 - voltage applied to the motor,
- voltage applied to the motor, 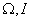 - motor speed and current,
- motor speed and current, 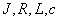 - motor parameters, respectively, inertia moment, resistance and inductance of the armature winding, design factor.
- motor parameters, respectively, inertia moment, resistance and inductance of the armature winding, design factor.
Getting the equation of state
Set the state and input vectors:
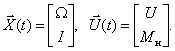
We get that 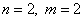 . We write the equation of state in expanded form for our case:
. We write the equation of state in expanded form for our case:
| (sixteen) |
Let us open matrix brackets in (16):
| (17) |
Let us bring the system of equations (15) to the form (17), using zero coefficients in the absence of a variable in the right-hand sides:
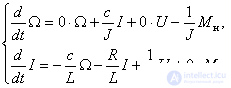
Now all the components of the parameter matrices are known, and you can write the equation of state in expanded form
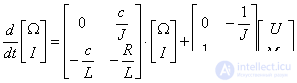 .
.
Therefore, the parameter matrices have the following form -
| (18) |
The definition of the characteristic equation of the object
The characteristic equation of the system is determined by the matrices of parameters of the equation of state (18), using the expression (7) -
| (nineteen) |
Substituting in (19) the expressions for the matrix of parameters 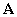 and the unit matrix
and the unit matrix 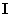 , we obtain the characteristic equation
, we obtain the characteristic equation
| (20) |
The definition of the transfer matrix of the object
We define the equivalent transfer function matrix, which connects the state and control vectors by expression (5), which in our case is:
| (21) |
Matrix 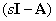 can be determined from (20)
can be determined from (20)
 .
.
Define the inverse matrix -
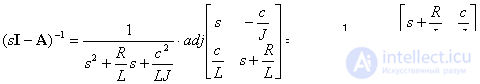 .
.
Finally we get -

Consequently, we obtain the transfer functions of the object.
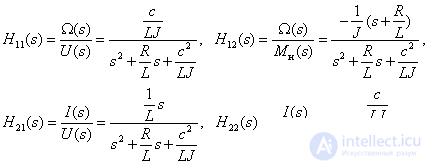
Test questions and tasks
Explain how the models are related to each other in the time and frequency domain?
How to determine the characteristic equation from the equation of state?
How to determine the system transfer function matrix by the equation of state?
According to the equation of state
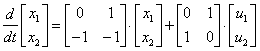 ,
,
describing a multidimensional system, determine the characteristic equation of the system.
Answer :
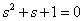 .
.
According to the equation of state
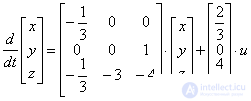 ,
,
describing a multidimensional system, determine the characteristic equation of the system.
Answer :
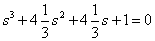 .
.
According to the equation of state
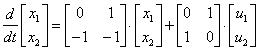 ,
,
describing the multidimensional system, determine the matrix of the transfer functions of the system.
Answer:
 .
.
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control