Lecture
The frequency response of a dynamic link is the function of a complex argument. 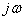 obtained by formal substitution
obtained by formal substitution 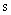 on
on 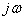 in terms of transfer function
in terms of transfer function
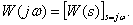
We obtain the relationship of the frequency response with well-known concepts. To do this, consider the dynamic link with the transfer function 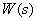 and signals
and signals 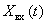 ,
, 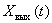 . Let be
. Let be 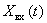 ,
, 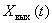 - absolutely integrable functions and equal to zero when
- absolutely integrable functions and equal to zero when 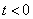 . Then the frequency spectra of these signals (Fourier transform) of these functions can be defined as follows:
. Then the frequency spectra of these signals (Fourier transform) of these functions can be defined as follows:
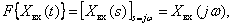
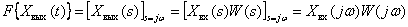 .
.
We obtain the ratio of the spectra
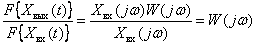 .
.
Thus, the frequency response of a dynamic link can be defined as the ratio of the spectrum (Fourier transform) of the output signal to the spectrum of the input signal.
Knowledge of the frequency response of the link allows you to determine the output spectrum on the input
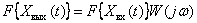 .
.
Consider a dynamic link -
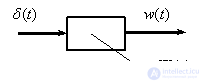
Fig. one
Get the spectrum of the output signal - impulse response
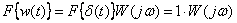 .
.
Then we have
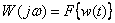 ,
,
that is, the Fourier transform of the impulse response is equal to the frequency response of the dynamic link.
The frequency function characteristic as a function of a complex argument can be represented as follows: -
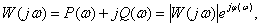
Where 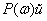 - real (real) part
- real (real) part 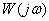 ,
,
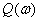 - imaginary part
- imaginary part 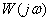 ,
,
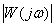 - module (amplitude)
- module (amplitude) 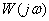 ,
,
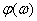 - phase argument
- phase argument 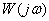 .
.
Amplitude, phase, real and imaginary parts of the frequency response are functions of the frequency, so the frequency response is used and graphically represented as amplitude-phase, real, imaginary, amplitude and phase frequency characteristics.
In the theory of automatic control, the following frequency characteristics of dynamic links are considered and used:
Amplitude-frequency response (AFC) -
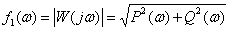 .
.
Phase Frequency Response (FRF) -
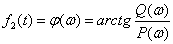 .
.
Real frequency response (VCHH) -
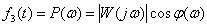 .
.
Imaginary frequency response (MCH) -
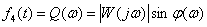 .
.
Amplitude-phase frequency response (AFC), which is defined as a hodograph (trace of the end movement) of the vector 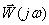 built on the complex plane when the frequency changes from 0 to
built on the complex plane when the frequency changes from 0 to 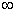 .
.
In fig. 2 we will show the frequency characteristics of some dynamic link.

Fig. 2
To clarify the physical meaning of the frequency response, we consider a dynamic link with the transfer function 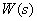 and impulse response
and impulse response 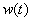 whose input is a harmonic signal
whose input is a harmonic signal 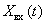 .
.
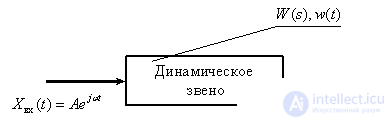
Fig. 3
Recall that the solution of a linear differential equation of a dynamic link, in the framework of the classical method, consists of two components — free and steady-state.
The steady-state component in the case of a harmonic function of time on the right side of the equation is also a harmonic function of time. Therefore, the steady-state signal at the output of the dynamic link can be described by the following expression
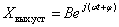 .
.
The signal at the output of the link can be determined using the image multiplication theorem

The result is
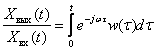 .
.
For transition to the established mode we suppose 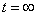 then we get
then we get
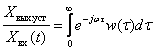 .
.
But, on the other hand, we have, by definition, the direct Fourier transform
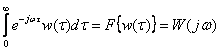 .
.
therefore
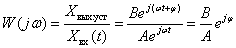 .
.
From here follows a simple algorithm for experimentally determining the frequency response of a linear dynamic link, object or control system for a specific frequency.  :
:
Apply a sinusoidal frequency signal to the object input  and constant amplitude.
and constant amplitude.
Wait until the free component of the transient decays.
Measure the amplitude of the output signal and its phase shift relative to the input signal.
The ratio of the amplitude of the output steady-state signal to the amplitude of the input signal will determine the modulus of the frequency response at a frequency 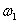 .
.
The phase shift of the output signal relative to the input signal will determine the angle (argument) of the frequency response at a frequency 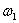 .
.
Using this algorithm for frequencies from zero to infinity, it is possible to experimentally determine the frequency response of a particular device. Functional diagram of the experimental setup for removing frequency characteristics is

Fig. four
At frequency 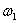 on the oscilloscope screen, after the free component is attenuated, the following picture -
on the oscilloscope screen, after the free component is attenuated, the following picture -
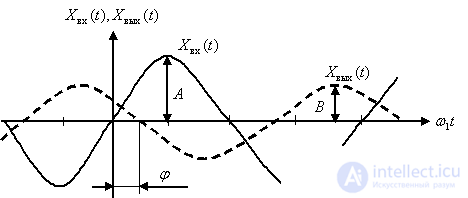
Fig. five
Based on fig. 5, a point belonging to the frequency characteristic of the device can be built on the complex plane, and the set of points when the frequency changes from zero to the value when the amplitude of the output steady-state signal becomes negligible will be an amplitude-phase frequency response (AFC). As can be seen from the figure, any necessary frequency response of the device can be constructed from these data.

Fig. 6
For experimental acquisition of frequency characteristics of various objects, specialized devices are used in engineering practice, and recently personal computers equipped with specialized I / O boards and application packages are widely used for such purposes.
Given all the above, it becomes clear and the physical meaning of the frequency response.
It shows how many times the dynamic link (device) operating in steady state changes, the amplitude of the input sinusoid of frequency 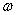 , and at what angle shifts the input sinusoid in phase.
, and at what angle shifts the input sinusoid in phase.
Test questions and tasks
How to determine the frequency response of a dynamic link, if its transfer function is known?
What types of frequency characteristics do you know?
How to determine the amplitude and frequency response argument?
List the main stages of experimental removal of the frequency response of the device.
Explain the physical meaning of the frequency response of the linear dynamic link.
Determine the expression of the frequency response for a given transfer function
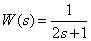 .
.
Answer :
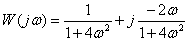 .
.
Determine the expression of the frequency response for a given transfer function
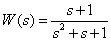 .
.
Answer :
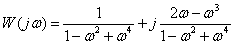 .
.
Determine the expression of the amplitude and phase frequency characteristics for the dynamic link with the transfer function -
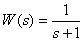 .
.
Answer :
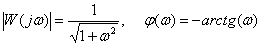 .
.
To the input of a dynamic link with transfer function
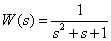 ,
,
constant amplitude harmonic signal with frequency
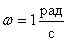 .
.
At what angle will the output signal be shifted in steady state?
Answer :
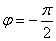
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control