The normal form is a relation property in the relational data model, which characterizes it in terms of redundancy, potentially leading to logically erroneous results of sampling or changing data. A normal form is defined as the set of requirements that a relation must satisfy.

The process of transforming database relations into a form that responds to normal forms is called normalization. Normalization is intended to bring the database structure to a form that provides minimal logical redundancy, and is not intended to reduce or increase productivity or reduce or increase the physical size of the database. [1] The ultimate goal of normalization is to reduce the potential inconsistency of information stored in the database. According to C. Deith, [2] the general purpose of the normalization process is as follows:

exclusion of some types of redundancy;
elimination of some update anomalies;
the development of a database project that is a fairly “high-quality” representation of the real world is intuitive and can serve as a good basis for further expansion;
simplifying the procedure for applying the necessary integrity constraints.
The elimination of redundancy is made, as a rule, due to the decomposition of relations in such a way that only primary facts are stored in each relation (that is, facts that cannot be derived from other stored facts).

Content
1 The role of normalization in the design of relational databases
2 Normal forms
2.1 First Normal Form (1NF)
2.2 Second normal form (2NF)
2.3 Third normal form (3NF)
2.4 Boyce Normal Form - Codd (BCNF)
2.5 Fourth normal form (4NF)
2.6 Fifth Normal Form (5NF)
2.7 Domain Key Normal Form (DKNF)
2.8 Sixth normal form (6NF)
3 Notes
4 See also
5 References
The role of normalization in the design of relational databases
While the ideas of normalization are very useful for designing databases, they are by no means a universal or exhaustive means of improving the quality of a database project. This is due to the fact that there is too much variety of possible errors and shortcomings in the structure of the database, which are not eliminated by normalization. Despite these arguments, the theory of normalization is a very valuable achievement of relational theory and practice, since it provides scientifically rigorous and reasonable criteria for the quality of a database project and formal methods for improving this quality. By this, the theory of normalization stands out sharply against the background of purely empirical approaches to design, [3] which are offered in other data models. Moreover, it can be argued that in the entire field of information technology there are practically no methods for assessing and improving design solutions that are comparable to the theory of normalizing relational databases in terms of formal rigor.

Normalization is sometimes blamed on the grounds that “this is just common sense,” and any competent professional himself will “naturally” design a fully normalized database without the need to apply dependency theory. [4] However, as K. Date points out, normalization is exactly the principles of common sense that guide a mature designer in his mind, that is, the principles of normalization are formalized common sense. Meanwhile, identifying and formalizing the principles of common sense is a very difficult task, and success in solving it is a significant achievement. [4]

Normal forms
Many scientists took part in the creation and development of the theory of normalization. However, the first three normal forms and the concept of functional dependence were proposed by E. Codd. [4]

First Normal Form (1NF)
Main article: First normal form
A relationship variable is in the first normal form (1NF) if and only if, in any valid value of a relationship, each tuple contains only one value for each of the attributes.

In a relational model, a relation is always in first normal form by definition of the concept of relation. As for the various tables, they may not be the correct representations of relations and, accordingly, may not be in 1NF.

Second normal form (2NF)
Main article: Second normal form
A relationship variable is in second normal form if and only if it is in first normal form, and each non-key attribute is irreducibly (functionally fully) dependent on its potential key.

Third normal form (3NF)
Main article: Third normal form
A relationship variable is in third normal form if and only if it is in second normal form, and there are no transitive functional dependencies of non-key attributes on key attributes.

Boyce Normal Form - Codd (BCNF)
Main article: Boyce Normal Form - Codd
A relation variable is in the normal form of Boys – Codd (otherwise, in a strengthened third normal form) if and only if each of its nontrivial and left irreducible functional dependencies has some potential key as its determinant.

Fourth normal form (4NF)
Main article: Fourth normal form
The relation variable is in fourth normal form if it is in Boyes – Codd normal form and does not contain non-trivial multivalued dependencies.

Fifth Normal Form (5NF)
Main article: Fifth normal form
A relationship variable is in the fifth normal form (otherwise, in a projection-connecting normal form) if and only if each nontrivial connection dependence in it is determined by the potential key (s) of this relationship.

Domain Key Normal Form (DKNF)
Main article: Domain-key normal form
Sixth normal form (6NF)
Main article: Sixth normal form
Introduced by C. Data in his book, [2] as a generalization of the fifth normal form for a temporal database.

The first normal form (1NF) is the basic normal form of the relation in the relational data model.

Content

• 1 Definition
• 2 Example
• 3 Atomicity of attributes
• 4 Initial assignment of 1NF
• 5 Notes
• 6 Literature

Definition

A relationship variable is in the first normal form if and only if, in any valid value of the relationship, each tuple contains only one value for each of the attributes.

In a relational model, a relation is always in first normal form by definition of the concept of relation .

As for the various tables , they may not be the correct representations of the relations and, accordingly, may not be in 1NF. In accordance with the definition of C. J. Data for such a case, the table is normalized (equivalently, it is in the first normal form) if and only if it is a direct and correct representation of some relation. More specifically, the table in question should satisfy the following five conditions:

1. There is no top-down ordering of lines (in other words, the order of the lines does not carry any information).
2. There is no left-to-right column ordering (in other words, the column order does not carry any information).
3. No duplicate rows.
4. Each row and column intersection contains exactly one value from the corresponding domain (and nothing more).
5. All columns are normal [1] .

The “normality” of all columns of a table means that there are no “hidden” components in the table that can only be accessed by calling some special operator instead of referring to the names of regular columns, or which lead to side effects for rows or tables when calling standard operators. Thus, for example, strings do not have identifiers other than the usual values ​​of potential keys (without hidden “string identifiers” or “object identifiers”). They also do not have hidden timestamps [1] .

Example

The original non-normalized (that is, not the correct representation of some relationship) table:

Employee	Phone number
Ivanov I.I.	283-56-82 390-57-34
Petrov P.P.	708-62-34

The table given to 1NF (which is the correct representation of some relationship):

Employee	Phone number
Ivanov I.I.	283-56-82
Ivanov I.I.	390-57-34
Petrov P.P.	708-62-34

Atomicity of attributes

The question of the atomicity of attributes is decided on the basis of the semantics of the data, that is, their semantic meaning. An attribute is atomic if its value loses its meaning during any partitioning or reordering. Therefore, if any method of splitting into parts does not deprive the attribute of meaning, then the attribute is not atomic.

The same value can be atomic or non-atomic, depending on the meaning of this value. For example, the value "4286" is

• atomic , if its meaning is “pin-code of a credit card” (when splitting or re-ordering, the meaning is lost)

• non-atomic if its meaning is “a set of numbers” ( no sense is lost when splitting or reordering)

A good way to decide whether it is necessary to split an attribute into parts is the question: “will the attribute parts be used separately?”. If so, then the attribute should be divided (but so that the meaningful parts of the attribute are preserved). Next, you need to ask again the same question for the new structure and so on until there are no attributes that can be split.

Examples of non-atomic attributes that are often encountered in practice: composite fields in the form of a string of identifiers separated by, say, commas: 100, 32, 168, 1045.

Initial assignment 1NF

The original purpose of 1NF, which was proposed by E.F. Codd in the article “The Relational Data Model for Large Shared Data Banks” [ 2] (“A Relational Model for the Large Shared Data Banks” [3] ), was not related at all to fight against anomalies or redundancy. Codd proposed using “simple domains” (simple domains) only to facilitate future software implementation, namely:

• to facilitate the storage of relations in the form of two-dimensional arrays

Attitude, all domains of which are simple, can be represented by storing a two-dimensional array with homogeneous columns.

Original text (English) [show]

• to facilitate data transfer in heterogeneous systems

The simplicity of the representation of relations by arrays, which is feasible if all relations are brought into normal form, provides advantages not only for storage, but also for transferring large amounts of data between systems that use largely different representations of data.

Original Text (eng.)

Second normal form

Main article: Normal form

The second normal form (eng. Second normal form ; abbreviated 2NF ) is one of the possible normal forms of relation in a relational database.

Content

[remove]

• 1 Definition
• 2 Example
• 3 Notes
• 4 Literature

Definition

A relationship variable is in second normal form if and only if it is in first normal form and each non-key attribute is irreducibly dependent on its potential key. [one]

Irreducibility means that there is no smaller subset of attributes in the composition of a potential key, from which this functional dependence can also be derived. [1] For the irreducible functional dependence, the equivalent concept “full functional dependence” is often used. [one]

If a potential key is simple, that is, consists of a single attribute, then any functional dependence on it is irreducible (complete). If a potential key is composite, then according to the definition of the second normal form in relation, there should be no non-key attributes depending on the part of the composite potential key.

The second normal form by definition forbids the presence of non-key attributes that are completely independent of the potential key. Thus, the second normal form, among other things, prohibits the creation of relations as unrelated (chaotic, random) attribute sets.

Example

An example of bringing a relationship to second normal form

In the following respect, let the primary key form a pair of attributes { Employee , Position }:

Employee	Position	Salary	Computer availability
Grishin	Storekeeper	20,000	Not
Vasiliev	Programmer	40,000	there is
Ivanov	Storekeeper	25,000	Not

Each employee sets the salary to the employee himself (although its boundaries depend on the position). The presence of a computer employee depends only on the position, that is, the dependence on the primary key is incomplete.

As a result of the reduction to 2NF, the initial relation should be decomposed into two relations:

Employee	Position	Salary
Grishin	Storekeeper	20,000
Vasiliev	Programmer	40,000
Ivanov	Storekeeper	25,000

Position	Computer availability
Storekeeper	Not
Programmer	there is

Third normal form

The third normal form (English Third normal form ; abbreviated 3NF ) is one of the possible normal forms of relation in a relational database. 3NF was originally formulated by E.F. Codd in 1971.

Content

• 1 Definition
• 2 "Nothing but the key"
• 3 Example
• 4 Notes
• 5 Literature
• 6 See also

Definition

The relation variable R is in 3NF if and only if the following conditions are true:

• R is in second normal form.
• No non-key attribute R is in transitive functional non-transitive dependence on potential key R.

Explanation of the definition:

The non-key attribute of the relationship R is an attribute that does not belong to any of the potential keys R.

The functional dependence of the attribute set Z on the attribute set X (written X → Z , pronounced “X defines z”) is transitive if there is a set of attributes Y such that X → Y and Y → Z. Moreover, none of the sets X , Y, and Z is a subset of the other, that is, the functional dependencies X → Z , X → Y, and Y → Z are not trivial .

The definition of 3NF, equivalent to Codd's definition, but differently formulated, was given by Carlo Zaniolo in 1982. According to him, a relationship variable is in 3NF if and only if for each of its functional dependencies X → A at least one of the following conditions is fulfilled:

• X contains A (that is, X → A is a trivial functional dependence)
• X - superkey
• A is a key attribute (that is, A is part of a potential key).

The definition of Zaniolo clearly defines the difference between the 3NF and the more stringent Beuys-Codd normal form (NFBC): the NFBC excludes the third condition (“A is the key attribute”).

"Nothing but the key"

A memorable and, by tradition, clear summary of Codd’s 3NF definition was given by Bill Kent: each non-key attribute “must provide information about a key, a full key, and nothing but a key.” [one]

The condition of dependence on the “full key” of non-key attributes ensures that the table is in the second normal form; and the condition of their dependence on “nothing but the key” is that they are in third normal form.

Chris Date talks about Kent’s summary as 3NF’s “intuitively attractive characterization”, and notes that with a slight change it can serve as a definition of a more strict Boyes-Codd normal form: “Each attribute must provide information about the key, the full key, and not except the key. The 3NF Kent definition is less stringent than the NFBK Data version, since the first one states only that non-key attributes depend on keys. Primary attributes (which are keys or their parts) should not be functionally dependent at all; each of them provides information about the key by providing the key itself or part of it. It should be noted here that this rule is valid only for non-key attributes, since applying it to all attributes will completely prohibit all complex alternative keys, since each element of such a key will violate the “full key” condition.

Example

Consider as an example the relationship that is in 2NF, but does not correspond to 3NF:

R1

Employee	Department	Phone
Grishin	Accounting	11-22-33
Vasiliev	Accounting	11-22-33
Petrov	Supply	44-55-66

In relation to the attribute "Employee" is the primary key. Employees have no personal phone numbers, and the employee’s phone number depends solely on the department.

Thus, in relation to the following functional dependencies exist: Employee → Department, Department → Telephone, Employee → Telephone.

Dependency Employee → Telephone is transitive, therefore, the relationship is not in 3NF.

As a result of the separation of the relationship R1, two relations are obtained that are in 3NF:

R2

Department	Phone
Accounting	11-22-33
Supply	44-55-66

R3

Employee	Department
Grishin	Accounting
Vasiliev	Accounting
Petrov	Supply

The initial relationship R1, if necessary, is easily obtained as a result of the operation of combining the relations R2 and R3.

Notes

Boyce Normal Form - Codd

The current version of the page has not yet been tested by experienced participants and may differ significantly from the version tested on March 15, 2013; checks require 10 edits.

Boyce-Codd normal form (English Boyce-Codd normal form ; abbreviated as BCNF ) is one of the possible normal forms of relation in the relational data model.

Sometimes, the normal form of Boys-Codd is called the enhanced third normal form , since it is stronger in all respects (stricter) than the previously determined 3NF [1] .

Named after Ray Beuys and Edgar Codd, although Christopher Deith points out that the strict definition of the “third” normal form, equivalent to the definition of the Beuys-Codd normal form, was first given by Ian Heath in 1971, therefore данную форму следовало бы называть «нормальной формой Хита» [1] .

Content

[remove]

• 1 Определение
• 2 Пример
• 3 Notes
• 4 Literature

Definition

Переменная отношения находится в BCNF тогда и только тогда, когда каждая её нетривиальная и неприводимая слева функциональная зависимость имеет в качестве своего детерминанта некоторый потенциальный ключ [1] .

Менее формально, переменная отношения находится в нормальной форме Бойса-Кодда тогда и только тогда, когда детерминанты всех ее функциональных зависимостей являются потенциальными ключами.

Для определения BCNF следует понимать понятие функциональной зависимости атрибутов отношения.

Пусть R является переменной отношения, а X и Y — произвольными подмножествами множества атрибутов переменной отношения R . Y функционально зависимо от X тогда и только тогда, когда для любого допустимого значения переменной отношения R , если два кортежа переменной отношения R совпадают по значению X , они также совпадают и по значению Y . Подмножество X называют детерминантом, а Y — зависимой частью.

Функциональная зависимость тривиальна тогда и только тогда, когда ее правая (зависимая) часть является подмножеством ее левой части (детерминанта).

Ситуация, когда отношение будет находиться в 3NF, но не в BCNF, возникает, например, при условии, что отношение имеет два (или более) потенциальных ключа, которые являются составными и имеют общий атрибут. На практике такая ситуация встречается достаточно редко, для всех прочих отношений 3NF и BCNF эквивалентны.

Example

Предположим, создаётся таблица бронирования для теннисных кортов на день: {Номер корта, Время начала, Время окончания, Тариф, Член клуба} . Тариф зависит от выбранного корта и членства в клубе, для каждого из кортов имеется тариф для членов теннисного клуба и для сторонних клиентов. Тарифы для кортов не повторяются.

Таким образом, возможны следующие составные первичные ключи: {Номер корта, Время начала} , {Номер корта, Время окончания} , {Тариф, Время начала} , {Тариф, Время окончания} .

Таблица соответствует второй и третьей нормальной форме. Требования второй нормальной формы (2NF) выполняются, так как все атрибуты входят в какой-то из потенциальных ключей, а неключевых атрибутов в отношении нет. Также нет и транзитивных зависимостей, что соответствует требованиям третьей нормальной формы (3NF).

Тем не менее, существует функциональная зависимость тарифа от номера корта. То есть, по ошибке можно нарушить логическую целостность и, например, приписать тариф Premium для первого корта, хотя тариф Premium может относиться только ко второму корту.

Можно улучшить структуру, разбив таблицу на две: {Номер корта, Время начала, Время окончания} и {Тариф, Номер корта, Член клуба} . Данное отношение будет соответствовать BCNF.

Четвёртая нормальная форма

Четвёртая нормальная форма (4NF) — одна из возможных нормальных форм отношения реляционной базы данных.

Content

[remove]

• 1 Определение
• 2 Пример
• 3 Notes
• 4 Literature

Definition

Переменная отношения R находится в четвёртой нормальной форме, если она находится в НФБК и все нетривиальные многозначные зависимости фактически являются функциональными зависимостями [1] от её потенциальных ключей.

Эквивалентная формулировка определения:

Переменная отношения R находится в четвёртой нормальной форме тогда и только тогда, когда в случае существования таких подмножеств A и B атрибутов этой переменной отношения R , для которых выполняется нетривиальная многозначная зависимость A →→ B , все атрибуты переменной отношения R также функционально зависят от А [2] .

Example

Предположим, что рестораны производят разные виды пиццы, а службы доставки ресторанов работают только в определенных районах города. Составной первичный ключ соответствующей переменной отношения включает три атрибута: {Ресторан, Вид пиццы, Район доставки} .

Такая переменная отношения не соответствует 4НФ, так как существует следующая многозначная зависимость:

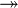• {Ресторан} {Вид пиццы}
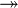• {Ресторан} {Район доставки}

То есть, например, при добавлении нового вида пиццы придется внести по одному новому кортежу для каждого района доставки. Возможна логическая аномалия, при которой определенному виду пиццы будут соответствовать лишь некоторые районы доставки из обслуживаемых рестораном районов.

Для предотвращения аномалии нужно декомпозировать отношение, разместив независимые факты в разных отношениях. В данном примере следует выполнить декомпозицию на {Ресторан, Вид пиццы} и {Ресторан, Район доставки} .

Однако если к исходной переменной отношения добавить атрибут, функционально зависящий от потенциального ключа, например цену с учётом стоимости доставки ( {Ресторан, Вид пиццы, Район доставки} → Цена ), то полученное отношение будет находиться в 4НФ и его уже нельзя подвергнуть декомпозиции без потерь. [ источник не указан 691 день ] Указанные выше многозначные зависимости в данном случае называются внедрёнными зависимостями .

Пятая нормальная форма (5NF) — одна из возможных нормальных форм отношения реляционной базы данных.

Content

[remove]

• 1 Определение
  • 1.1 Декомпозиция без потерь
  • 1.2 Зависимость соединения
  • 1.3 Формулировка определения
• 2 Свойства 5НФ
• 3 Пример
• 4 Notes
• 5 Literature

Definition

Для определения пятой нормальной формы следует предварительно ввести понятие зависимости соединения , которое, в свою очередь основано на понятии декомпозиции без потерь .

Декомпозиция без потерь

Декомпозицией [1] отношения R называется замена R на совокупность отношений { R 1 , R 2 ,... , R n } такую, что каждое из них есть проекция R , и каждый атрибут R входит хотя бы в одну из проекций декомпозиции.

Например, для отношения R с атрибутами { a , b , c } существуют следующие основные варианты декомпозиции:

• { a }, { b }, { c }
• { a }, { b , c }
• { a , b }, { c }
• { b }, { a , c }
• { a , b }, { b , c }
• { a , b }, { a , c }
• { b , c }, { a , c }
• { a , b }, { b , c }, { a , c }

Рассмотрим теперь отношение R' , которое получается в результате операции естественного соединения (NATURAL JOIN), применённой к отношениям, полученным в результате декомпозиции R .

Декомпозиция называется декомпозицией без потерь , если R' в точности совпадает с R .

Неформально говоря, при декомпозиции без потерь отношение «разделяется» на отношения-проекции таким образом, что из полученных проекций возможна «сборка» исходного отношения с помощью операции естественного соединения.

Далеко не всякая декомпозиция является декомпозицией без потерь. Проиллюстрируем это на примере отношения R с атрибутами { a , b , c }, приведённом выше. Пусть отношение R имеет вид:

R

a	b	c
Moscow	Russia	столица
Tomsk	Russia	не столица
Berlin	Germany	столица

Декомпозиция R 1 = { a }, R 2 = { b , c } имеет вид:

R 1

a
Moscow
Tomsk
Berlin

R 2

b	c
Russia	столица
Russia	не столица
Germany	столица

Результат операции соединения этих отношений:

R' = R 1 NATURAL JOIN R 2

a	b	c
Moscow	Russia	столица
Moscow	Russia	не столица
Moscow	Germany	столица
Tomsk	Russia	столица
Tomsk	Russia	не столица
Tomsk	Germany	столица
Berlin	Russia	столица
Berlin	Russia	не столица
Berlin	Germany	столица

Очевидно, что R' не совпадает с R , а значит такая декомпозиция не является декомпозицией без потерь. Рассмотрим теперь декомпозицию R 1 = { a , b }, R 2 = { a , c }:

R 1

a	b
Moscow	Russia
Tomsk	Russia
Berlin	Germany

R 2

a	c
Moscow	столица
Tomsk	не столица
Berlin	столица

Такая декомпозицией является декомпозицией без потерь, в чём читатель может убедиться самостоятельно.

В некоторых случаях отношение вовсе невозможно декомпозировать без потерь. Существуют также примеры отношений, для которых нельзя выполнить декомпозицию без потерь на две проекции, но которые можно подвергнуть декомпозиции без потерь на три или большее количество проекций [2] .

Зависимость соединения

Пусть R — переменная отношения, а A , B , ..., Z — некоторые подмножества множества ее атрибутов.

Если декомпозиция любого допустимого значения R на отношения, состоящие из множеств атрибутов A , B , ..., Z , является декомпозицией без потерь, говорят, что переменная отношения R удовлетворяет зависимости соединения *{А, В, . . . , Z} [3] .

Иными словами, переменная отношения R удовлетворяет зависимости соединения *{А, В, . . . , Z} тогда и только тогда, когда любое допустимое значение переменной отношения R эквивалентно соединению ее проекций по подмножествам A , B , ..., Z множества атрибутов.

Подобно тому, как функциональная зависимость есть частный случай многозначной зависимости , многозначная зависимость является частным случаем зависимости соединения . Зависимость соединения является предельным обобщением понятий многозначной и функциональной зависимости, то есть это наиболее общая форма зависимости между атрибутами отношения.

Важно понимать, что зависимость соединения определяется не для конкретного значения переменной отношения в тот или иной момент времени, а по всем возможным значениям. Поэтому понятие зависимости соединения определено не для отношения (конкретного значения), а для переменной отношения . Зависимость соединения определяется не механически по текущим значениям, а следует из внешнего знания о природе и закономерностях данных, которые могут находиться в переменной отношения. То же самое относится к многозначной и функциональной зависимостям.

Зависимость соединения *{A, B,..., Z} является тривиальной тогда и только тогда, когда по крайней мере одно из подмножеств A , B , ..., Z является множеством всех атрибутов отношения (включает все атрибуты). В противном случае зависимость соединения является нетривиальной .

Формулировка определения

Отношение находится в пятой нормальной форме (иначе — в проекционно-соединительной нормальной форме) тогда и только тогда, когда каждая нетривиальная зависимость соединения в нём определяется потенциальным ключом (ключами) этого отношения [2] .

Зависимость соединения *{A, B,..., Z} определяется потенциальным ключом (ключами) тогда и только тогда, когда каждое из подмножеств A , B , ..., Z множества атрибутов является суперключом отношения [2] .

Условие «каждое из подмножеств A, B,..., Z множества атрибутов является суперключом отношения» можно эквивалентно сформулировать так: «каждое из подмножеств A , B , ..., Z множества атрибутов включает некоторый потенциальный ключ отношения».

Свойства 5НФ

Любое отношение в 5НФ автоматически находится также в 4НФ и, следовательно, во всех других нормальных формах. 5НФ является окончательной нормальной формой (по крайней мере в контексте операций проекции и соединения).

Рональд Фейгин в 1979 г. показал, что любая переменная отношения может быть подвергнута декомпозиции без потерь на эквивалентный набор переменных отношения в 5НФ, т.е. 5НФ всегда достижима. Однако К. Дейт отмечает, что процедура определения того, что некоторая переменная отношения находится в 4НФ, а не в 5НФ, и, таким образом, существует возможность её дальнейшей выгодной декомпозиции, всё ещё остаётся не вполне ясной. Это связано с тем, что задача определения всех зависимостей соединения для отношения может оказаться очень сложной, а по поводу отношения можно утверждать, что оно находится в 5НФ, только при условии известности всех его потенциальных ключей и всех его зависимостей соединения.

Очень редко отношение, находящееся в 4НФ, не соответствует 5НФ. Это те ситуации, в которых реальные правила, ограничивающие допустимые комбинации атрибутов, никак не выражены в структуре отношения (см. пример ниже). В таком случае, если отношение не приведено к 5НФ, бремя обеспечения логической целостности данных отчасти перекладывается на приложение, отвечающее за добавление, удаление и изменения данных. В этом случае существует риск возникновения ошибок. Пятая нормальная форма исключает возникновение таких аномалий.

Example

Предположим, что нужно хранить данные об ассортименте нескольких продавцов, торгующих продукцией нескольких фирм (номенклатура товаров фирм может пересекаться):

Ассортимент (продавцы, фирмы, товары)

Seller	Фирма	Товар
Иванов	Рога и Копыта	Пылесос
Иванов	Рога и Копыта	Хлебница
Petrov	Безенчук&Ко	Сучкорез
Petrov	Безенчук&Ко	Пылесос
Petrov	Безенчук&Ко	Хлебница
Petrov	Безенчук&Ко	Umbrella
Sidorov	Безенчук&Ко	Пылесос
Sidorov	Безенчук&Ко	Telescope
Sidorov	Рога и Копыта	Пылесос
Sidorov	Рога и Копыта	Lamp
Sidorov	Hercules	Вешалка

Если дополнительных условий нет, то данное отношение, которое находится в 4-ой нормальной форме, является корректным и отражает все необходимые ограничения.

Now suppose you need to take into account the following restriction: each seller has in his assortment a limited list of firms and a limited list of types of goods and offers products from the list of goods produced by firms from the list of firms .

That is, the seller does not have the right to trade in any goods of any firms. If seller P has the right to trade in goods of firm F , and if seller P has the right to trade in goods of type T , then the seller’s assortment of P includes goods of type T of firm F , provided that firm F produces goods of type T.

Such a restriction may be caused, for example, by the fact that the list of types of goods of a seller is limited by its licenses, or by the knowledge and qualifications necessary for their sale, and the list of firms of each seller is determined by partnership agreements.

In this example, in particular, it is assumed that the seller Ivanov has the right to trade in goods only of the company “Horns and Hoofs”, the seller Petrov - in goods only of the company “Bezenchuk & Co”, but the seller Sidorov does not have the right to trade bread and with *** cuts and tons .d

The relation proposed above cannot exclude situations in which this restriction will be violated. Nothing prevents to enter data on trade in goods that this company does not release at all, or data on trade in goods of the company that the seller does not serve, or data on trade in such type of goods that the seller does not have the right to sell.

The relation is not in 5NF, because it has a non-trivial connection dependence * {{Seller, Firm}, {Firm, Product}, {Seller, Product}}, however, the subsets {Seller, Firm}, {Firm, Product}, {Seller , Commodity} are not super keys of the original relationship

In this case, to bring to 5NF, the relationship should be divided into three: {Seller, Firm} , {Firm, Product} , {Seller, Product} .

Merchants goods

Seller	Product
Ivanov	A vacuum cleaner
Ivanov	Bread box
Petrov	Lopper
Petrov	A vacuum cleaner
Petrov	Bread box
Petrov	Umbrella
Sidorov	Telescope
Sidorov	A vacuum cleaner
Sidorov	Lamp
Sidorov	Hanger

Sellers firms

Seller	Firm
Ivanov	Horns and hooves
Petrov	Bezenchuk & Co.
Sidorov	Bezenchuk & Co.
Sidorov	Horns and hooves
Sidorov	Hercules

Company Products

Firm	Product
Horns and hooves	A vacuum cleaner
Horns and hooves	Bread box
Horns and hooves	Lamp
Bezenchuk & Co.	Lopper
Bezenchuk & Co.	A vacuum cleaner
Bezenchuk & Co.	Bread box
Bezenchuk & Co.	Umbrella
Bezenchuk & Co.	Telescope
Hercules	Hanger

Domain Key Normal Form

The current version of the page has not yet been tested by experienced participants and may differ significantly from the version tested on December 1, 2011; checks require 3 edits.

The domain key normal form (DKNF) is one of the possible normal forms of the relational database table. She was offered by Ronald Fagin in 1981.

Definition

A relationship variable is in DK / NF if and only if every constraint imposed on it is a logical consequence of domain constraints and key constraints imposed on a given relationship variable.

Domain Restriction - a restriction that requires you to use for a particular attribute values ​​only from a certain specified domain. The restriction is essentially the task of specifying a list (or logical equivalent of a list) of valid values ​​of a type and declaring that the specified attribute has a given type.

Key constraint is a constraint stating that some attribute or combination of attributes is a potential key.

Any relationship variable that is in DK / NF is necessarily in 5NF. However, not any relationship variable can be brought to DK / NF.

Sixth normal form

The sixth normal form (6NF) is one of the possible normal forms of the relational database table.

Introduced by K. Data as a generalization of the fifth normal form for a chronological database [1] .

Content

[remove]

• 1 Definition
• 2 Example
• 3 Notes
• 4 Literature

Definition

A relationship variable is in the sixth normal form if and only if it satisfies all the non-trivial dependencies of the connection. It follows from the definition that a variable is in 6NF if and only if it is irreducible, that is, it cannot be subjected to further lossless decomposition. Each relationship variable that is in 6NF is also in 5NF.

Example

The idea of ​​“decomposition to the end” was put forward before the start of research in the field of historical data, but did not find support. However, for historical databases, the maximum possible decomposition allows you to combat redundancy and simplifies maintaining the integrity of the database.

For historical databases, U_ operators are defined, which unpack the relations by the specified attributes, perform the corresponding operation, and package the result obtained. In this example, the connection of the relationship projections should be made using the operator U_JOIN.

Workers

Tab. No	Time	Position	Home address
6575	[01-01-2000: 10-02-2003]	locksmith	st. Lenin, 10
6575	[11-02-2003: 15-06-2006]	locksmith	st. Soviet, 22
6575	[16-06-2006: 05-03-2009]	brigadier	st. Soviet, 22

The variable “Employees” is not in 6NF and can be decomposed into the variable relationships “Employees 'Positions” and “Employers' Home Addresses”.

Employees positions Tab. No Time Position 6575 [01-01-2000: 15-06-2006] locksmith 6575 [16-06-2006: 05-03-2009] brigadier

Employees' home addresses Tab. No Time Home address 6575 [01-01-2000: 10-02-2003] st. Lenin, 10 6575 [11-02-2003: 05-03-2009] st. Soviet, 22

Normalization database simple language

In short, what is normalization? Most modern subd are developed on the basis of relational algebra, which appeared before the relational subd themselves under the authorship of a certain doctor Codd. He also derived several rules, or forms, for organizing data and their relationships. In total, there are 6 + two such forms out of the competition, Beuys-Codd and domain-key.

In practice, it is rarely normalized beyond the 3rd normal form. In more detail to learn about all normal forms and the theory under links in the bottom of a post.

All examples from the book are shown in the database for a forum with the usual structure for forums - posts, authors, time, etc.

Here is the diagram before the conversion.

Keys

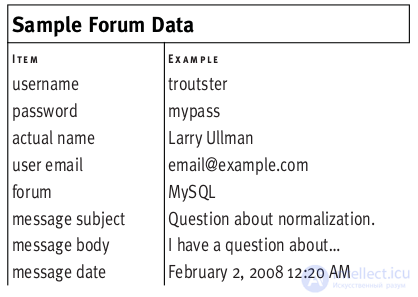
Keys are part of normalized tables. There are two types - external and primary.

A primary key is a unique identifier that meets the following conditions:

1. It must have a value, not NULL.
2. Be unchanged - the key value should not change.
3. Have a unique value for each line.

Foreign keys are references to the primary keys of other tables that satisfy the conditions above.

To start normalization, you must specify at least one primary key. In the example, this will be the message ID.

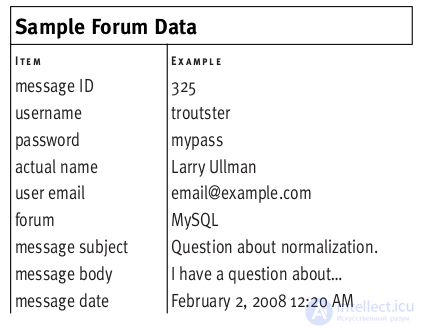
To specify a primary key, you need to find a field that will fit all three conditions. If there is no such field, it must be created. Ideally, the field should be of type integer.

Relations

Relationships are pointers that show how data in one table relates to data in another. Simply put, a link from one column of the first table to another column of the second table. There are three types - one-to-one, one-to-many, many-to-many.

The one-to-one ratio means that field1 is related to field2. An example is each person has their own passport number. 1 person - 1 passport. There is a one-to-one relationship.

One-to-many indicates that field1 can relate to both field2 and field3, fieldN ... The book gives an example - one man can have many women and vice versa Author humorist One-to-many is the most common connection between tables in normalized databases.

A many-to-many relationship occurs when several values ​​from one table correspond to several values ​​from another table. For example, in a blog category there can be many posts, and a blog can have many categories. Such an attitude may also occur in composite keys. Such a connection should be avoided because it leads to data redundancy. In the same WordPress category and posts are correlated through the third table - wp_relationships.

The figure shows the legend of all three relations in the UML notation.

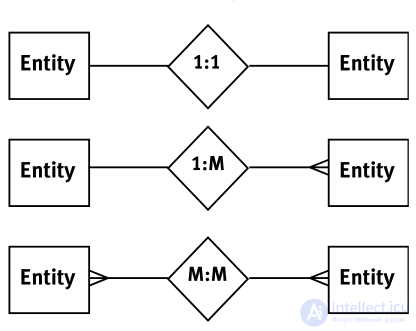
Creating a database structure (schema) and relationships between tables can be accelerated using various CASE-tools. At the end there will be a link to mysql workbench, a free cross-platform program.

First normal form

As stated above, normalization is bringing the database structure in order in accordance with several rules. The rules need to be followed precisely, and it is necessary to lead to the forms in the order they are followed.

To bring the table to 1NF, you need to follow two rules:

1. Atomicity or indivisibility. Each column must contain one indivisible value.
2. The table should not contain duplicate columns or groups of data.

For example, if a table contains the full address of a person in one field (street, city, postal code), it will not meet the 1NF rules, because it will contain different values ​​in one column, which would be a violation of the atomicity rule. Or if the database contains data about films and there are columns of actor1, actor2, actor3 in it, also will not meet the rules, since there will be a repetition of data.

It is necessary to start normalization with checking the structure of the database for compatibility with 1NF. All columns that are not atomic should be divided into their constituent columns. If the table has duplicate columns, then they need to select a separate table.

To bring the table to the first normal form, you should:

• Find all fields that contain multi-part information. In the figure above, the message date field contains the day, month, year, and time, which can be broken down into its component parts, but in this example, such detailing of the date is not needed. Mysql can work with this format - thanks to the DATETIME type. In this example, the username is split into a first and last name. Other examples of unsuccessful decisions can be fields in which all the phones of a person (mobile, work) or his interests (cooking, dancing) are stored at once.
• Those data that can be broken into its component parts must be put into separate fields. In the picture above, the full name is distributed in the name and surname.
• Take out duplicate data in a separate table. In the example with the forum there is no such problem, so we take as an example a table containing information about films. There are several actor fields that are repeatable. Repeated fields here carry two problems. If you store information about the actors in this way, their number will be limited by the number of tables. Even if there are 100 of them, it will still be the limit for some films. And the second problem - there will be a large number of empty (NULL) cells for most other entries, which should also be avoided. The solution to this problem will be to create a separate table for the actors, where information about all the necessary films will be entered. The names of the actors are also broken up to honor atomicity. Also in this table is its primary key, which is a prerequisite for normalization.
• Double check that all tables fit the conditions of the first normal form.

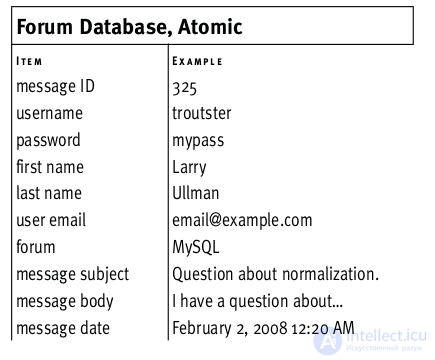
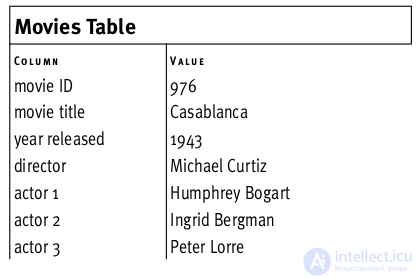
problem of redundant fields

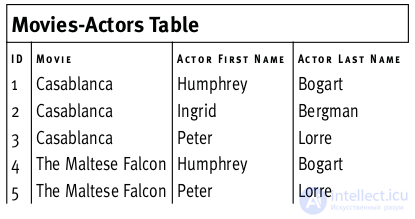
solving the problem of redundant fields

Tips

• The easiest way to bring to 1NF is to go through the eyes on all the columns. Check each row for repetition of similar data and divisibility.
• Different sources interpret the process of normalization in their own, mostly drier, technical language. The result of normalization is more important than the repetition of rules and buzzwords.

The next post will be devoted to the second normal form - 2NF.

The second normal form.

To bring the tables to the second normal form (2NF), the tables should be already in 1NF. Normalization should be in order.

Now, in the second normal form, the condition must be met - any column that is not a key (including an external one) must depend on the primary key. Usually such columns that have values ​​that are independent of the key are easy to identify. If the data contained in the column is not related to the key that describes the row, then they should be separated into their own separate table. In the old table it is necessary to return the primary key.

In the picture above, the names of the films and the names of the actors violate the 2NF rules (they are not keys themselves and do not depend on the primary key).

After all conversions, the database with movies will have at least 4 tables.

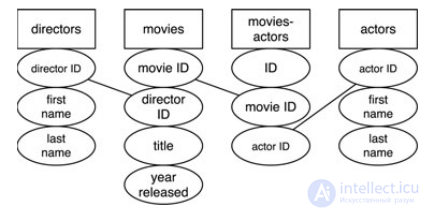
To bring bd to the second normal form, it took 4 tables. Directors (directors) are represented in movies (movies) through the foreign key director ID, movies in the table are movie actors (movies-actors) through movie ID, actors through actor ID

Each director name, picture name and actor name is stored only once and all non-key fields depend on the primary key of their own table.

In fact, normalization can be exaggeratedly called the process of creating more and more new tables until redundancy and repetition is completely destroyed.

To bring the base to the second normal form, you need:

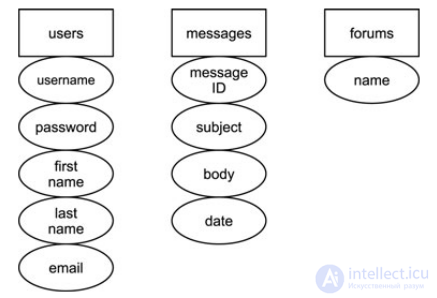
To bring this base to 2NF, you need 3 tables minimum

• Identify all columns that are not directly dependent on the primary key of this table. In the figure above, the users and forums tables do not have a primary key. The messages table has a primary key - the message ID, on which all other fields in this table depend.
• We create the necessary fields in the users and forums tables, select from the existing fields, or create new primary keys from the new ones.
  

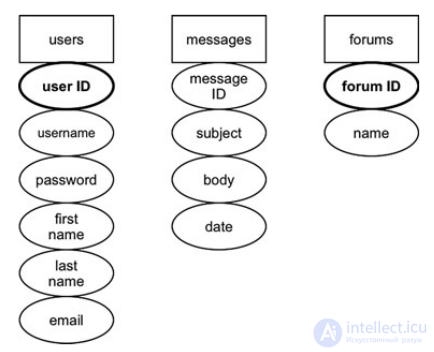
  Each table needs its own primary key.

• Create foreign keys and denote their relationships between tables. The final step of normalization to 2NF will be the allocation of foreign keys for communication with associated tables. The primary key of one table must be a foreign key in another. The figure below shows the relationship between the keys of the three tables. The user ID field of the messages table is the primary key of the user ID field of the users table. The type of connection between them is one to many. One user can leave many messages, but a message can have only one user. The same link connects the forums and messages tables via the forum ID. A forum can have many messages, but a message can only be in one forum.

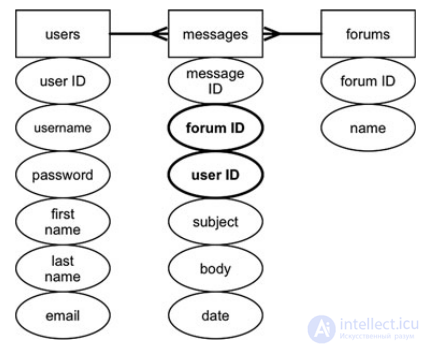
To correlate three tables, two foreign keys have been added to messages leading to primary keys in their tables.

Tips:

• Another way to bring the schema to 2NF is to look at the relationships between the tables. The ideal option is to create all one-to-many relationships. The many-to-many relationships of the species need restructuring.
• If you look again at the movies-actors table, you will notice that it is an intermediate table. It turns the many-to-many relationship between movies and actors into one-to-many. You can enter such intermediate tables, in which all columns are keys. These tables do not require their own primary key, since it can be a combination of two foreign keys.
• A properly normalized table will never have duplicate rows (two or more rows whose values ​​are not keys and contain matching data).
• To simplify normalization, remember that when casting to 1NF, you look for doubles horizontally (double columns), and when casting to 2NF - you look vertically (double lines).

The third normal form.

The database will be in third normal form if it is reduced to the second normal form and each non-key column is independent of each other. If you follow the normalization process correctly to this point, with the reduction to 3NF there may be no questions. You should know that 3NF is violated, if changing the value in one column, you will need to change in another column. In the example with the forum (figure above), problems with the reduction to 3NF will not arise, but we can consider a hypothetical situation where this may occur as an example.

Take, as a sample, a single table that stores some information about business customers: name, surname, phone number, address, city, state, zip code, and so on. Such a table will not be located in 3NF, since there will be many fields interdependently - the street will depend on the city, the city from the state, the postal code is also in question. All of these fields will be subordinate to each other, and not to the person to whom this record belongs.

To normalize such a database, you need to create a table for the states, cities (with a foreign key leading to the state table) and for postal codes. All of them will refer back to the client table.

If you feel that all these actions may be superfluous, you are right. Honestly, in the upper levels of normalization is often not necessary. The point is that you need to try to normalize the database, but sometimes you have to make concessions in order to avoid excessive complication. The needs of the application and the data structure in the database will tell you how much the normalization process will be required.

As already mentioned, the example with the forum is already quite normalized, but we still describe the steps for normalization for the third normal form, showing how to fix the example with clients.

To bring the base to the third normal form, it is necessary:

1. Определить, в каких полях каких таблиц имеется взаимозависимость. Как только что говорилось, поля, которые зависят больше друг от друга (как город от штата), чем от ряда в целом. В базе форума такой проблемы нет. Взглянув на таблицу сообщений, увидите, что каждый заголовок, каждое тело сообщения относится к своему message ID.

2. Создайте соответствующие таблицы. Если есть проблемный столбец в шаге 1, создавайте раздельные таблицы для него. Как города и штаты, в примере с клиентами.

3. Создайте или выделите первичные ключи. Каждая таблица должна иметь первичный ключ. Для примера с клиентами это будут city ID и state ID.

4. Создайте необходимые внешние ключи, которые образуют любое из отношений. В нашем примере нужно добавить state ID в таблицу городов и city ID в таблицу клиентов. Это свяжет каждого клиента с городом и штатом, где они живут.

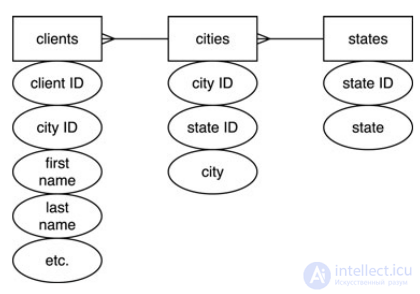
Рассмотренная в качестве примера база данных с записями о клиентах, созданы две новых таблицы для хранения информации о городах и штатах.

Подсказки:

Вообще, можно было бы и не нормализовывать базу с клиентами до такой степени. Если оставить города и штаты в таблице клиентов, самое страшное, что могло бы случиться — если бы город изменил название, нужно было бы менять его во всех записях о клиентах, которые живут в этом городе. Но города редко меняют свои имена.

Несмотря на то, что имеются правила как нормализовывать базы данных, разные люди сделают это разными способами. Проектирование баз данных допускает личные предпочтения и интерпретации. Важно, чтобы в базе не было явных нарушений нормальных форм, которые могут привести в дальнейшем к проблемам.

Нарушения правил нормализации

Убедившись, что база данных в 3НФ поможет гарантировать надёжность и жизнеспособность, не нужно полностью нормализовывать все базу, с которыми вы работаете. Перед тем, как использовать эти методы, имейте ввиду, что это может иметь долгосрочные разрушающие последствия.

Две основных причины, чтобы нарушить правила нормализации — удобство и быстродействие. Меньшим число таблиц проще управлять, чем большим. Кроме того, из-за более сложного характера, нормализованные таблицы более медленные для обновления, изменения и выдачи данных. Вкратце, нормализация это сделка между целостностью/расширяемостью и простотой/скоростью. С другой стороны, есть достаточно способов чтобы улучшить производительность базы данных, но не так много способов чтобы исправить повреждённые данные, возникшие из-за плохого дизайна структуры.

Практика и опыт подскажут, как сделать модель базы данных, но лучше совершайте ошибки пробуя нормальные формы, хотя бы до тех пор, пока не поймете принцип.

See also

• Integrity constraints