5. Elements of the SQL language

This chapter discusses the elements of the SQL (Structured Query Language) language. The current version of the SQL language standard was adopted in 1992 (The official name of the standard is the International Standard Database Language SQL (1992), the unofficial name is SQL / 92, or SQL-92, or SQL2). The document describing the standard contains more than 600 pages. We will give only some concepts of the language.

The SQL language has become the de facto standard language for accessing databases. All DBMSs claiming the name "relational" implement one or another SQL dialect. Many non-relational systems also currently have access to relational data. The goal of standardization is the portability of applications between different DBMSs.

It should be noted that currently, no system implements the SQL standard in full. In addition, in all dialects of the language there are possibilities that are not standard. Thus, it can be said that each dialect is a superset of some subset of the SQL standard. This complicates the portability of applications developed for some DBMS to other DBMS.

The SQL language uses terms that are slightly different from the terms of the relational theory, for example, instead of "relations", "tables" are used, instead of "tuples" - "rows", instead of "attributes" - "columns" or "columns".

The standard of the SQL language, although it is based on the relational theory, but in many places it departs from it. For example, a relation in a relational data model does not allow the same tuples, and tables in SQL terminology can have the same rows. There are other differences.

The SQL language is relationally complete. This means that any relational algebra operator can be expressed by a suitable SQL statement.

SQL statements

The basis of the SQL language is made up of operators that are conditionally divided into several groups according to the functions they perform.

The following groups of statements can be distinguished (not all SQL statements are listed):

DDL (Data Definition Language) Operators - Database Object Definition Operators

• CREATE SCHEMA - create database schema
• DROP SHEMA - remove database schema
• CREATE TABLE - create table
• ALTER TABLE - change table
• DROP TABLE - delete table
• CREATE DOMAIN - create domain
• ALTER DOMAIN - change domain
• DROP DOMAIN - delete domain
• CREATE COLLATION - create a sequence
• DROP COLLATION - delete sequence
• CREATE VIEW - create view
• DROP VIEW - delete view

DML (Data Manipulation Language) Operators - Data Manipulation Operators

• SELECT - select rows from tables
• INSERT - add rows to the table
• UPDATE - change rows in the table
• DELETE - delete rows in the table.
• COMMIT - commit changes
• ROLLBACK - roll back changes

Data Protection and Management Operators

• CREATE ASSERTION - create constraint
• DROP ASSERTION - remove restriction
• GRANT - grant privileges to a user or application to manipulate objects.
• REVOKE - revoke user or application privileges

In addition, there are groups of statements for setting session parameters, obtaining information about the database, static SQL statements, dynamic SQL statements.

Most important to the user are data manipulation statements (DML).

Examples of using data manipulation operators

INSERT - insert rows into a table

Example 1 Insert a single row into the table:

  INSERT INTO
   P (PNUM, PNAME)
   VALUES (4, "Ivanov");

Example 2 Inserting into the table several rows selected from another table (data about suppliers from table P with numbers greater than 2 are inserted into the TMP_TABLE table):

  INSERT INTO
   TMP_TABLE (PNUM, PNAME)
   SELECT PNUM, PNAME
     FROM P
     WHERE P.PNUM> 2;

UPDATE - update rows in a table

Example 3 Update multiple rows in a table:

  UPDATE P
   SET PNAME = "Guns"
   WHERE P.PNUM = 1;

DELETE - delete rows in a table.

Example 4 Deleting multiple rows in a table:

  DELETE FROM P
   WHERE P.PNUM = 1;

Example 5 Delete all rows in the table:

  DELETE FROM P;

Examples of using the SELECT statement

The SELECT statement is actually the most important for the user and the most complex SQL statement. It is designed to select data from tables, i.e. he, in fact, implements one of the main purposes of the database - to provide information to the user.

The SELECT statement is always executed on some tables in the database.

Remark In fact, databases can contain not only permanently stored tables, but also temporary tables and so-called views. Views are simply SELECT data stored in a database. From the point of view of users, a view is a table that is not stored permanently in the database, but “arises” at the moment of accessing it. From the point of view of the SELECT statement, both constantly stored tables and temporary tables and views look exactly the same. Of course, the actual execution of a SELECT statement by the system takes into account the differences between stored tables and views, but these differences are hidden from the user.

The result of the SELECT statement is always a table. Thus, according to the results of actions, the SELECT statement is similar to the relational algebra operators. Any relational algebra operator can be expressed by a suitably formulated SELECT statement. The complexity of the SELECT statement is determined by the fact that it contains all the capabilities of relational algebra, as well as additional features that are not in relational algebra.

Selection of data from one table

Example 6 Select all data from the supplier table ( SELECT keywords ... FROM ...):

  SELECT *
   FROM P;

Remark As a result, we obtain a new table containing a complete copy of the data from the original table P.

Example 7 Select all rows from the table of suppliers that satisfy a certain condition (keyword WHERE ...):

  SELECT *
   FROM P
   WHERE P.PNUM> 2;

Remark As a condition in the WHERE clause, you can use complex logical expressions that use table fields, constants, comparisons (>, <, =, etc.), brackets, AND and OR unions, NOT negation.

Example 8 Select some columns from the source table (specifying the list of columns to be selected):

  SELECT P.NAME
   FROM P;

Remark As a result, we obtain a table with a single column containing all the names of suppliers.

Remark If there are several suppliers in the source table with different numbers but the same names, then the resulting table will contain rows with repetitions - duplicate rows are not automatically discarded.

Example 9 Select some columns from the source table by removing duplicate rows from the result (keyword DISTINCT ):

  SELECT DISTINCT P.NAME
   FROM P;

Remark Using the DISTINCT keyword causes the result table to delete all duplicate rows.

Example 10 Using scalar expressions and column renames in queries (keyword AS ...):

  SELECT
     TOVAR.TNAME,
     TOVAR.KOL,
     TOVAR.PRICE,
     "=" AS EQU,
     TOVAR.KOL * TOVAR.PRICE AS SUMMA
   FROM TOVAR;

As a result, we get a table with columns that were not in the original TOVAR table:

TNAME	KOL	PRICE	EQU	SUMMA
Bolt	ten	100	=	1000
Nut	20	200	=	4,000
Screw	thirty	300	=	9000

Example 11. Ordering query results ( ORDER BY keyword ...):

  SELECT
     PD.PNUM,
     PD.DNUM,
     PD.VOLUME
   FROM PD
   ORDER BY DNUM;

As a result, we obtain the following table, ordered by the DNUM field:

PNUM	DNUM	VOLUME
one	one	100
2	one	150
3	one	1000
one	2	200
2	2	250
one	3	300

Example 12 Ordering query results by several fields in ascending or descending order (keywords ASC , DESC ):

  SELECT
     PD.PNUM,
     PD.DNUM,
     PD.VOLUME
   FROM PD
   ORDER BY 
     DNUM ASC,
     VOLUME DESC;

As a result, we will get a table in which the lines go in ascending order of the value of the DNUM field, and the rows with the same value of DNUM go in descending order of the value of the VOLUME field:

PNUM	DNUM	VOLUME
3	one	1000
2	one	150
one	one	100
2	2	250
one	2	200
one	3	300

Remark If the keywords ASC or DESC are not indicated explicitly, then the default ordering is ascending (ASC).

Selection of data from several tables

Example 13 Natural joining of tables (method 1 - explicit indication of joining conditions):

  SELECT
     P.PNUM,
     P.PNAME,
     PD.DNUM,
     PD.VOLUME
   FROM P, PD
   WHERE P.PNUM = PD.PNUM;

As a result, we obtain a new table in which the rows with data on suppliers are connected with the rows with data on the supply of parts:

PNUM	PNAME	DNUM	VOLUME
one	Ivanov	one	100
one	Ivanov	2	200
one	Ivanov	3	300
2	Petrov	one	150
2	Petrov	2	250
3	Sidorov	one	1000

Remark The joined tables are listed in the FROM clause of the statement, the join condition is given in the WHERE clause. Section WHERE, in addition to the conditions of joining tables, may also contain the conditions for selecting rows.

Example 14 Natural joining of tables (method 2 - keywords JOIN ... USING ... ):

  SELECT
     P.PNUM,
     P.PNAME,
     PD.DNUM,
     PD.VOLUME
   FROM P JOIN PD USING PNUM;

Remark The USING keyword allows you to explicitly indicate which of the common table columns will be joined.

Example 15 Natural joining of tables (method 3 - the keyword NATURAL JOIN ):

  SELECT
     P.PNUM,
     P.PNAME,
     PD.DNUM,
     PD.VOLUME
   FROM P NATURAL JOIN PD;

Remark The FROM section does not indicate which fields are being connected. NATURAL JOIN automatically connects across all the same fields in the tables.

Example 16 The natural connection of the three tables:

  SELECT
     P.PNAME,
     D.DNAME,
     PD.VOLUME
   FROM
     P NATURAL JOIN PD NATURAL JOIN D;

As a result, we obtain the following table:

PNAME	DNAME	VOLUME
Ivanov	Bolt	100
Ivanov	Nut	200
Ivanov	Screw	300
Petrov	Bolt	150
Petrov	Nut	250
Sidorov	Bolt	1000

Example 17 Direct work of tables:

  SELECT
     P.PNUM,
     P.PNAME,
     D.DNUM,
     D.DNAME
   FROM P, D;

As a result, we obtain the following table:

PNUM	PNAME	DNUM	DNAME
one	Ivanov	one	Bolt
one	Ivanov	2	Nut
one	Ivanov	3	Screw
2	Petrov	one	Bolt
2	Petrov	2	Nut
2	Petrov	3	Screw
3	Sidorov	one	Bolt
3	Sidorov	2	Nut
3	Sidorov	3	Screw

Remark Because the condition of joining the tables is not indicated, then each row of the first table will be connected with each row of the second table.

Example 18 Connection of tables by an arbitrary condition. Consider the tables of suppliers and details that are assigned a statue (see Example 8 from the previous chapter):

PNUM	PNAME	PSTATUS
one	Ivanov	four
2	Petrov	one
3	Sidorov	2

Table 1 P ratio (Suppliers)

DNUM	DNAME	DSTATUS
one	Bolt	3
2	Nut	2
3	Screw	one

Table 2 Attitude D (Details)

The answer to the question "which suppliers have the right to supply what parts?" gives the following query:

  SELECT
     P.PNUM,
     P.PNAME,
     P.PSTATUS,
     D.DNUM,
     D.DNAME,
     D.DSTATUS
   FROM P, D
   WHERE P.PSTATUS> = D.DSTATUS;

As a result, we obtain the following table:

PNUM	PNAME	PSTATUS	DNUM	DNAME	DSTATUS
one	Ivanov	four	one	Bolt	3
one	Ivanov	four	2	Nut	2
one	Ivanov	four	3	Screw	one
2	Petrov	one	3	Screw	one
3	Sidorov	2	2	Nut	2
3	Sidorov	2	3	Screw	one

Use of correlation names (aliases, pseudonyms)

Sometimes you have to execute queries in which a table joins with itself, or one table joins twice with another table. At the same time, correlation names ( aliases , pseudonyms ) are used, which allow to distinguish the joined copies of tables. Correlation names are entered in the FROM section and are spaced after the table name. Correlation names should be used as a prefix in front of the column name and separated from the column name by a dot. If the query contains the same fields from different instances of the same table, they must be renamed to eliminate ambiguity in the naming of the columns of the resulting table. The definition of the correlation name is valid only during the execution of the query.

Example 19 Select all pairs of suppliers in such a way that the first supplier in the pair has a status greater than the status of the second supplier:

  SELECT
     P1.PNAME AS PNAME1,
     P1.PSTATUS AS PSTATUS1,
     P2.PNAME AS PNAME2,
     P2.PSTATUS AS PSTATUS2
   FROM
     P P1, P P2
   WHERE P1.PSTATUS1> P2.PSTATUS2;

As a result, we obtain the following table:

PNAME1	PSTATUS1	PNAME2	PSTATUS2
Ivanov	four	Petrov	one
Ivanov	four	Sidorov	2
Sidorov	2	Petrov	one

Example 20 Consider a situation where some suppliers (let's call their counterparties) can act both as suppliers of parts and as recipients. Tables storing data may have the following form:

Counterparty number NUM	Name of counterparty NAME
one	Ivanov
2	Petrov
3	Sidorov

Table 3 Attitudes of CONTRAGENTS

Detail number DNUM	the name of detail DNAME
one	Bolt
2	Nut
3	Screw

Table 4 Attitude DETAILS (Details)

Vendor number PNUM	Recipient's number CNUM	Detail number DNUM	Quantity supplied VOLUME
one	2	one	100
one	3	2	200
one	3	3	300
2	3	one	150
2	3	2	250
3	one	one	1000

Table 5 CD Ratio (Supply)

In the CD (delivery) table, the PNUM and CNUM fields are foreign keys that refer to the potential NUM key in the CONTRAGENTS table.

The answer to the question "who supplies what to whom in what quantity" is given by the following request:

  SELECT
     P.NAME AS PNAME,
     C.NAME AS CNAME,
     DETAILS.DNAME,
     CD.VOLUME
   FROM
     CONTRAGENTS P,
     CONTRAGENTS C,
     DETAILS,
     CD
   WHERE
     P.NUM = CD.PNUM AND
     C.NUM = CD.CNUM AND
     D.DNUM = CD.DNUM;

As a result, we obtain the following table:

Supplier name PNAME	Recipient Name CNAME	the name of detail DNAME	Quantity supplied VOLUME
Ivanov	Petrov	Bolt	100
Ivanov	Sidorov	Nut	200
Ivanov	Sidorov	Screw	300
Petrov	Sidorov	Bolt	150
Petrov	Sidorov	Nut	250
Sidorov	Ivanov	Bolt	1000

Remark The same query can be expressed in a very large number of ways, for example, like this:

  SELECT
     P.NAME AS PNAME,
     C.NAME AS CNAME,
     DETAILS.DNAME,
     CD.VOLUME
   FROM
     CONTRAGENTS P,
     CONTRAGENTS C,
     DETAILS NATURAL JOIN CD
   WHERE
     P.NUM = CD.PNUM AND
     C.NUM = CD.CNUM;

Using aggregate functions in queries

Example 21 Get the total number of suppliers (keyword COUNT ):

  SELECT COUNT (*) AS N
   FROM P;

As a result, we obtain a table with one column and one row containing the number of rows from table P:

N
3

Example 22 Get the total, maximum, minimum and average number of parts supplied (keywords SUM , MAX , MIN , AVG ):

  SELECT
     SUM (PD.VOLUME) AS SM,
     MAX (PD.VOLUME) AS MX,
     MIN (PD.VOLUME) AS MN,
     AVG (PD.VOLUME) AS AV
   FROM PD;

As a result, we get the following table with one line:

SM	MX	MN	AV
2000	1000	100	333.33333333

Using aggregate functions with groupings

Example 23 For each part, get the total quantity supplied (keyword GROUP BY ...):

  SELECT
     PD.DNUM,
     SUM (PD.VOLUME) AS SM
   GROUP BY PD.DNUM;

This query will be executed as follows. First, the rows in the source table will be grouped so that each group contains rows with the same DNUM values. Then within each group the VOLUME field will be summarized. From each group one line will be included in the resulting table:

DNUM	SM
one	1250
2	450
3	300

Remark In the list of selectable fields of the SELECT statement containing the GROUP BY clause, only aggregate functions and fields that are part of the grouping condition can be included. The following query will generate a syntax error:

  SELECT
     PD.PNUM,
     PD.DNUM,
     SUM (PD.VOLUME) AS SM
   GROUP BY PD.DNUM;

The reason for the error is that the PNUM field is included in the list of selected fields, which is not included in the GROUP BY section. Indeed, each received group of lines can include several lines with different values ​​of the PNUM field. One final line will be formed from each group of lines. At the same time, there is no unequivocal answer to the question of what value to choose for the PNUM field in the summary line.

Remark Some SQL dialects do not consider this an error. The query will be executed, but it is impossible to predict what values ​​will be entered in the PNUM field in the result table.

Example 24 Obtain part numbers whose total quantity supplied exceeds 400 (keyword HAVING ...):

Remark The condition that the total quantity supplied must be greater than 400 cannot be stated in the WHERE section, since in this section you cannot use aggregate functions. Conditions using aggregate functions should be placed in a special section HAVING:

  SELECT
     PD.DNUM,
     SUM (PD.VOLUME) AS SM
   GROUP BY PD.DNUM
   HAVING SUM (PD.VOLUME)> 400;

As a result, we obtain the following table:

DNUM	SM
one	1250
2	450

Remark In a single query, both the conditions for selecting rows in the WHERE section and the conditions for selecting groups in the HAVING section may occur. Group selection conditions cannot be moved from the HAVING section to the WHERE section. Similarly, row selection conditions cannot be moved from the WHERE section to the HAVING section, except for conditions that include fields from the GROUP BY group list.

Using subqueries

A very convenient tool that allows you to formulate queries in a more understandable way is the ability to use subqueries nested in the main query.

Example 25 Get a list of suppliers whose status is less than the maximum status in the table of suppliers (comparison with a subquery):

  SELECT *
   FROM P
   WHERE P.STATYS <
     (SELECT MAX (P.STATUS)
         FROM P);

Remark Because If the P.STATUS field is compared with the result of a subquery, the subquery must be formulated to return a table consisting of exactly one row and one column .

Remark The result of the query will be equivalent to the result of the following sequence of actions:

1. Run the nested subquery once and get the maximum status value.
2. Scan the table of suppliers P, each time comparing the value of the status of the supplier with the result of the subquery, and select only those rows in which the status is less than the maximum.

Example 26 Using the IN predicate. Get a list of suppliers that supply part number 2:

  SELECT *
   FROM P
   WHERE P.PNUM IN
     (SELECT DISTINCT PD.PNUM
         FROM PD
         WHERE PD.DNUM = 2);

Remark In this case, the nested subquery may return a table containing several rows.

Remark The result of the query will be equivalent to the result of the following sequence of actions:

1. Run the subquery once and get the list of vendor numbers that supply part number 2.
2. Scan the table of suppliers P, each time checking if the number of the supplier is contained in the result of the subquery.

Example 27 Using the predicate exist . Get a list of suppliers that supply part number 2:

  SELECT *
   FROM P
   WHERE EXIST
     (SELECT *
         FROM PD
         WHERE
             PD.PNUM = P.PNUM AND
             PD.DNUM = 2);

Remark The result of the query will be equivalent to the result of the following sequence of actions:

1. Scan the table of suppliers P, each time performing a subquery with a new value of the supplier number taken from table P.
2. In the result of the query, include only those rows from the supplier table for which the nested subquery returned a non-empty set of rows.

Remark Unlike the two previous examples, the subquery contains a parameter (external link) transmitted from the main request — the vendor number P.PNUM. Such subqueries are called correlated . An external link can take on different values ​​for each candidate row evaluated by a subquery, so the subquery must be re-executed for each row selected in the main query. Such subqueries are characteristic of the EXIST predicate, but can be used in other subqueries.

Remark It may seem that queries containing correlated subqueries will execute more slowly than queries with uncorrelated subqueries. In fact, this is not the case. how the user formulated the request does not determine how this request will be executed. The SQL language is non-procedural, but declarative. This means that the user formulating the query simply describes what the result of the query should be , and how this result will be obtained - the DBMS itself is responsible for this.

Example 28 Using the predicate NOT EXIST . Get a list of suppliers that do not supply part number 2:

  SELECT *
   FROM P
   WHERE NOT EXIST
     (SELECT *
         FROM PD
         WHERE
             PD.PNUM = P.PNUM AND
             PD.DNUM = 2);

Remark As in the previous example, a correlated subquery is used here. Отличие в том, что в основном запросе будут отобраны те строки из таблицы поставщиков, для которых вложенный подзапрос не выдаст ни одной строки.

Пример 29 . Получить имена поставщиков, поставляющих все детали:

 SELECT DISTINCT PNAME
  FROM P
  WHERE NOT EXIST
    (SELECT *
        FROM D
        WHERE NOT EXIST
          (SELECT *
              FROM PD
               WHERE
                  PD.DNUM = D.DNUM AND
                  PD.PNUM = P.PNUM));

Remark Данный запрос содержит два вложенных подзапроса и реализует реляционную операцию деления отношений .

Самый внутренний подзапрос параметризован двумя параметрами (D.DNUM, P.PNUM) и имеет следующий смысл: отобрать все строки, содержащие данные о поставках поставщика с номером PNUM детали с номером DNUM. Отрицание NOT EXIST говорит о том, что данный поставщик не поставляет данную деталь. Внешний к нему подзапрос, сам являющийся вложенным и параметризованным параметром P.PNUM, имеет смысл: отобрать список деталей, которые не поставляются поставщиком PNUM. Отрицание NOT EXIST говорит о том, что для поставщика с номером PNUM не должно быть деталей, которые не поставлялись бы этим поставщиком. Это в точности означает, что во внешнем запросе отбираются только поставщики, поставляющие все детали.

Использование объединения, пересечения и разности

Пример 30 . Получить имена поставщиков, имеющих статус, больший 3 или поставляющих хотя бы одну деталь номер 2 (объединение двух подзапросов - ключевое слово UNION ):

 SELECT P.PNAME
  FROM P
  WHERE P.STATUS > 3
   UNION
  SELECT P.PNAME
    FROM P, PD
    WHERE P.PNUM = PD.PNUM AND
        PD.DNUM = 2;

Remark Результатирующие таблицы объединяемых запросов должны быть совместимы, т.е. иметь одинаковое количество столбцов и одинаковые типы столбцов в порядке их перечисления. Не требуется , чтобы объединяемые таблицы имели бы одинаковые имена колонок. Это отличает операцию объединения запросов в SQL от операции объединения в реляционной алгебре. Наименования колонок в результатирующем запросе будут автоматически взяты из результата первого запроса в объединении.

Пример 31 . Получить имена поставщиков, имеющих статус, больший 3 и одновременно поставляющих хотя бы одну деталь номер 2 (пересечение двух подзапросов - ключевое слово INTERSECT ):

 SELECT P.PNAME
  FROM P
  WHERE P.STATUS > 3
  INTERSECT
  SELECT P.PNAME
    FROM P, PD
    WHERE P.PNUM = PD.PNUM AND
        PD.DNUM = 2;

Пример 32 . Получить имена поставщиков, имеющих статус, больший 3, за исключением тех, кто поставляет хотя бы одну деталь номер 2 (разность двух подзапросов - ключевое слово EXCEPT ):

 SELECT P.PNAME
  FROM P
  WHERE P.STATUS > 3
EXCEPT
  SELECT P.PNAME
    FROM P, PD
    WHERE P.PNUM = PD.PNUM AND
        PD.DNUM = 2;

Синтаксис оператора выборки данных (SELECT)

BNF-нотация

Опишем синтаксис оператора выборки данных (оператора SELECT) более точно. При описании синтаксиса операторов обычно используются условные обозначения, известные как стандартные формы Бэкуса-Наура ( BNF ).

В BNF обозначениях используются следующие элементы:

• Символ "::=" означает равенство по определению. Слева от знака стоит определяемое понятие, справа - собственно определение понятия.
• Ключевые слова записываются прописными буквами. Они зарезервированы и составляют часть оператора.
• Метки-заполнители конкретных значений элементов и переменных записываются курсивом.
• Необязательные элементы оператора заключены в квадратные скобки [].
• Вертикальная черта | указывает на то, что все предшествующие ей элементы списка являются необязательными и могут быть заменены любым другим элементом списка после этой черты.
• Фигурные скобки {} указывают на то, что все находящееся внутри них является единым целым.
• Троеточие "…" означает, что предшествующая часть оператора может быть повторена любое количество раз.
• Многоточие, внутри которого находится запятая ".,.." указывает, что предшествующая часть оператора, состоящая из нескольких элементов, разделенных запятыми, может иметь произвольное число повторений. Запятую нельзя ставить после последнего элемента. Замечание: данное соглашение не входит в стандарт BNF, но позволяет более точно описать синтаксис операторов SQL.
• Круглые скобки являются элементом оператора.

Синтаксис оператора выборки

В довольно сильно упрощенном виде оператор выборки данных имеет следующий синтаксис (для некоторых элементов мы дадим не BNF-определения, а словесное описание):

Оператор выборки ::=
Table expression
[ ORDER BY
{{ Имя столбца-результата [ ASC | DESC ]} | { Положительное целое [ ASC | DESC ]}}.,..];

Табличное выражение ::=
Select-выражение
[
{ UNION | INTERSECT | EXCEPT } [ ALL ]
{ Select-выражение | TABLE Имя таблицы | Конструктор значений таблицы }
]

Select-выражение ::=
SELECT [ ALL | DISTINCT ]
{{{ Скалярное выражение | Функция агрегирования | Select-выражение } [ AS Имя столбца ]}.,..}
| {{ Имя таблицы | Имя корреляции }.*}
| *
FROM {
{ Имя таблицы [ AS ] [ Имя корреляции ] [( Имя столбца .,..)]}
| { Select-выражение [ AS ] Имя корреляции [( Имя столбца .,..)]}
| Соединенная таблица }.,..
[ WHERE Условное выражение ]
[ GROUP BY {[{ Имя таблицы | Имя корреляции }.] Имя столбца }.,..]
[ HAVING Условное выражение ]

Remark Select-выражение в разделе SELECT, используемое в качестве значения для отбираемого столбца, должно возвращать таблицу, состоящую из одной строки и одного столбца, т.е. скалярное выражение.

Remark Условное выражение в разделе WHERE должно вычисляться для каждой строки, являющейся кандидатом в результатирующее множество строк. В этом условном выражении можно использовать подзапросы. Синтаксис условных выражений, допустимых в разделе WHERE рассматривается ниже.

Remark Раздел HAVING содержит условное выражение, вычисляемое для каждой группы, определяемой списком группировки в разделе GROUP BY. Это условное выражение может содержать функции агрегирования, вычисляемые для каждой группы. Условное выражение, сформулированное в разделе WHERE, может быть перенесено в раздел HAVING. Перенос условий из раздела HAVING в раздел WHERE невозможен, если условное выражение содержит агрегатные функции. Перенос условий из раздела WHERE в раздел HAVING является плохим стилем программирования - эти разделы предназначены для различных по смыслу условий (условия для строк и условия для групп строк).

Remark Если в разделе SELECT присутствуют агрегатные функции, то они вычисляются по-разному в зависимости от наличия раздела GROUP BY. Если раздел GROUP BY отсутствует, то результат запроса возвращает не более одной строки. Агрегатные функции вычисляются по всем строкам, удовлетворяющим условному выражению в разделе WHERE. Если раздел GROUP BY присутствует, то агрегатные функции вычисляются по отдельности для каждой группы, определенной в разделе GROUP BY.

Скалярное выражение - в качестве скалярных выражений в разделе SELECT могут выступать либо имена столбцов таблиц, входящих в раздел FROM, либо простые функции, возвращающие скалярные значения.

Функция агрегирования ::=
COUNT (*) |
{
{ COUNT | MAX | MIN | SUM | AVG } ([ ALL | DISTINCT ] Scalar Expression )
}

Table value constructor :: =
VALUES Line value constructor ., ..

String value constructor :: =
Constructor Element | ( Design element ., ..) | Select expression

Remark A select expression used in the string's value constructor is required to return exactly one string.

Constructor Element :: =
Expression to calculate the value | NULL | DEFAULT

Синтаксис соединенных таблиц

В разделе FROM оператора SELECT можно использовать соединенные таблицы. Пусть в результате некоторых операций мы получаем таблицы A и B. Такими операциями могут быть, например, оператор SELECT или другая соединенная таблица. Тогда синтаксис соединенной таблицы имеет следующий вид:

Соединенная таблица ::=
Перекрестное соединение
| Естественное соединение
| Соединение посредством предиката
| Соединение посредством имен столбцов
| Соединение объединения

Тип соединения ::=
INNER
| LEFT [ OUTER ]
| RIGTH [ OUTER ]
| FULL [ OUTER ]

Перекрестное соединение ::=
Таблица А CROSS JOIN Таблица В

Естественное соединение ::=
Таблица А [ NATURAL ] [ Тип соединения ] JOIN Таблица В

Соединение посредством предиката ::=
Таблица А [ Тип соединения ] JOIN Таблица В ON Предикат

Соединение посредством имен столбцов ::=
Таблица А [ Тип соединения ] JOIN Таблица В USING (Имя столбца.,..)

Соединение объединения ::=
Таблица А UNION JOIN Таблица В

Опишем используемые термины.

CROSS JOIN - Перекрестное соединение возвращает просто декартово произведение таблиц. Такое соединение в разделе FROM может быть заменено списком таблиц через запятую.

NATURAL JOIN - Естественное соединение производится по всем столбцам таблиц А и В, имеющим одинаковые имена. В результатирующую таблицу одинаковые столбцы вставляются только один раз.

JOIN … ON - Соединение посредством предиката соединяет строки таблиц А и В посредством указанного предиката.

JOIN … USING - Соединение посредством имен столбцов соединяет отношения подобно естественному соединению по тем общим столбцам таблиц А и Б, которые указаны в списке USING.

OUTER - Ключевое слово OUTER (внешний) не является обязательными, оно не используется ни в каких операциях с данными.

INNER - Тип соединения "внутреннее". Внутренний тип соединения используется по умолчанию, когда тип явно не задан. В таблицах А и В соединяются только те строки, для которых найдено совпадение.

LEFT (OUTER) - Тип соединения "левое (внешнее)". Левое соединение таблиц А и В включает в себя все строки из левой таблицы А и те строки из правой таблицы В, для которых обнаружено совпадение. Для строк из таблицы А, для которых не найдено соответствия в таблице В, в столбцы, извлекаемые из таблицы В, заносятся значения NULL.

RIGHT (OUTER) - Тип соединения "правое (внешнее)". Правое соединение таблиц А и В включает в себя все строки из правой таблицы В и те строки из левой таблицы А, для которых обнаружено совпадение. Для строк из таблицы В, для которых не найдено соответствия в таблице А, в столбцы, извлекаемые из таблицы А заносятся значения NULL.

FULL (OUTER) - Тип соединения "полное (внешнее)". Это комбинация левого и правого соединений. В полное соединение включаются все строки из обеих таблиц. Для совпадающих строк поля заполняются реальными значениями, для несовпадающих строк поля заполняются в соответствии с правилами левого и правого соединений.

UNION JOIN - Соединение объединения является обратным по отношению к внутреннему соединению. Оно включает только те строки из таблиц А и В, для которых не найдено совпадений. В них используются значения NULL для столбцов, полученных из другой таблицы. Если взять полное внешнее соединение и удалить из него строки, полученные в результате внутреннего соединения, то получится соединение объединения.

Использование соединенных таблиц часто облегчает восприятие оператора SELECT, особенно, когда используется естественное соединение. Если не использовать соединенные таблицы, то при выборе данных из нескольких таблиц необходимо явно указывать условия соединения в разделе WHERE. Если при этом пользователь указывает сложные критерии отбора строк, то в разделе WHERE смешиваются семантически различные понятия - как условия связи таблиц, так и условия отбора строк (см. примеры 13, 14, 15 данной главы).

Синтаксис условных выражений раздела WHERE

Условное выражение, используемое в разделе WHERE оператора SELECT должно вычисляться для каждой строки-кандидата, отбираемой оператором SELECT. Условное выражение может возвращать одно из трех значений истинности: TRUE, FALSE или UNKNOUN. Строка-кандидат отбирается в результатирующее множество строк только в том случае, если для нее условное выражение вернуло значение TRUE.

Условные выражения имеют следующий синтаксис (в целях упрощения изложения приведены не все возможные предикаты):

Условное выражение ::=
[ ( ] [ NOT ]
{ Предикат сравнения
| Between predicate
| In predicate
| Like predicate
| Null predicate
| Предикат количественного сравнения
| Предикат exist
| Предикат unique
| Предикат match
| Overlaps predicate }
[{ AND | OR } Conditional expression ] [)]
[ IS [ NOT ] { TRUE | FALSE | UNKNOWN }]

Comparison predicate :: =
String value constructor {= | <| > | | <= | > = | <>} String value constructor

Example 33 Comparison of table field and scalar value:

  POSTAV.VOLUME> 100 

Example 34 Comparison of two constructed lines:

  (PD.PNUM, PD.DNUM) = (1, 25) 

This example is equivalent to the conditional expression

  PD.PNUM = 1 AND PD.DNUM = 25 

Predicate between :: =
The constructor of the values ​​of the string [ NOT ] BETWEEN
String value constructor AND String value constructor

Example 35 PD.VOLUME BETWEEN 10 AND 100

The predicate in :: =
The constructor of the values ​​of the string [ NOT ] IN
{( Select-expression ) | (An expression to calculate the value ., ..)}

Example 36

  P.PNUM IN (SELECT PD.PNUM FROM PD WHERE PD.DNUM = 2) 

Example 37

  P.PNUM IN (1, 2, 3, 5) 

Like predicate :: =
Expression to calculate the search string value [ NOT ] LIKE
An expression to calculate the value of the template string [ ESCAPE Character ]

Remark The LIKE predicate searches for a search string in a pattern string. In the pattern string it is allowed to use two stencil characters:

• The underscore character "_" can be used instead of any single character in the search string,
• The percent character "%" can replace the set of any characters in the search string (the number of characters in the set can be from 0 or more).

Null predicate :: =
The constructor of the values ​​of the string IS [ NOT ] NULL

Comment. The NULL predicate is used specifically to test whether the expression being tested is not equal to a null value.

Quantitative comparison predicate :: =
String value constructor {= | <| > | | <= | > = | <>}
{ ANY | SOME | ALL } ( Select-expression )

Remark The quantifiers ANY and SOME are synonymous and are completely interchangeable.

Remark If one of the ANY and SOME quantifiers is specified, then the predicate of quantitative comparison returns TRUE if the compared value matches at least one value returned in the subquery (select expression).

Remark If the ALL quantifier is specified, the quantitative comparison predicate returns TRUE if the compared value matches each value returned in the subquery (select expression).

Example 38

  P.PNUM = SOME (SELECT PD.PNUM FROM PD WHERE PD.DNUM = 2) 

Exist predicate :: =
EXIST ( Select-expression )

Remark The EXIST predicate returns TRUE if the result of a subquery (select expression) is not empty.

Unique : = predicate
UNIQUE ( Select-expression )

Remark The UNIQUE predicate returns TRUE if there are no matching rows as a result of a subquery (select expression).

Match predicate :: =
MATCH string constructor [ UNIQUE ]
[ PARTIAL | FULL ] ( Select-expression )

Remark The MATCH predicate checks whether the value defined in the string constructor will match the value of any string resulting from the subquery.

Overlaps predicate :: =
OVERLAPS string value constructor

Remark The OVERLAPS predicate is a specialized predicate that allows you to determine whether a specified period of time overlap another period of time.

The order of the SELECT statement

In order to understand how the result of the execution of the SELECT statement is obtained, consider the conceptual scheme of its implementation. This scheme is precisely conceptual, since it is guaranteed that the result will be as if it were performed step by step in accordance with this scheme. In fact, the result is actually obtained by more sophisticated algorithms that a particular DBMS "owns".

Stage 1. Execution of a single SELECT statement

If the operator contains the keywords UNION, EXCEPT and INTERSECT, then the query is divided into several independent queries, each of which is performed separately:

Step 1 (FROM) . Calculates the direct Cartesian product of all tables specified in the mandatory FROM section. As a result of step 1, we obtain table A.

Step 2 (WHERE) . If the WHERE clause is present in the SELECT statement, then table A is scanned from step 1. In this case, the conditional expression given in the WHERE clause is calculated for each row from table A. Only those rows for which the conditional expression returns the value TRUE are included in the result. If the WHERE clause is omitted, then go straight to step 3. If nested subqueries participate in a conditional expression, then they are calculated in accordance with this conceptual scheme. As a result of step 2, we obtain table B.

Step 3 (GROUP BY) . If the GROUP BY clause is present in the SELECT statement, then the rows of table B obtained in the second step are grouped according to the grouping list listed in the GROUP BY clause. If the GROUP BY section is omitted, then go straight to step 4. As a result of step 3, we obtain Table C.

Step 4 (HAVING) . If the HAVING clause is present in the SELECT statement, then groups that do not satisfy the conditional clause given in the HAVING clause are excluded. If the HAVING section is omitted, then immediately proceed to step 5. As a result of step 4, we obtain table D.

Step 5 (SELECT) . Each group obtained in step 4 generates one result line as follows. All scalar expressions specified in the SELECT section are evaluated. According to the rules for using the GROUP BY clause, these scalar expressions must be the same for all rows within each group. For each group, the values ​​of the aggregate functions given in the SELECT section are calculated. If the GROUP BY clause was absent, but in the SELECT clause there are aggregate functions, then it is considered that there is only one group. If there is neither a GROUP BY clause nor aggregate functions, then it is considered that there are as many groups as there are lines selected at this time. As a result of step 5, we obtain table E, containing as many columns as the number of elements given in the SELECT section and as many rows as the selected groups.

Stage 2. Performing UNION, EXCEPT, INTERSECT operations

If the UNION, EXCEPT, and INTERSECT keywords were present in the SELECT statement, then the tables resulting from the execution of stage 1 are combined, subtracted, or intersected.

Stage 3. Streamlined results

If the ORDER BY clause is present in the SELECT statement, the rows from the previous steps in the table are ordered according to the ordering list in the ORDER BY clause.

How the SELECT statement actually executes

If you carefully consider the above conceptual algorithm for calculating the result of a SELECT statement, then it is immediately clear that it is extremely expensive to execute it directly in this form. Even at the very first step, when the Cartesian product of the tables given in the FROM section is calculated, a table of enormous dimensions can be obtained, and practically the majority of the rows and columns from it will be discarded in the next steps.

In fact, in the RDBMS there is an optimizer , whose function is to find such an optimal algorithm for executing a query that guarantees getting the correct result.

Schematically, the work of the optimizer can be represented as a sequence of several steps:

Step 1 (Parsing) . The incoming request is being parsed. At this step, it is determined whether the query is formulated at all (in terms of SQL syntax). During the parsing, some internally generated query is generated, which is used in subsequent steps.

Step 2 (Conversion to canonical form) . A request in the internal representation is transformed into a certain canonical form. When converting to canonical form, both syntactic and semantic transformations are used. Syntactic transformations (for example, converting logical expressions to conjunctive or disjunctive normal form, replacing the expressions "x AND NOT x" with "FALSE", etc.) allow you to get a new internal representation of the query, syntactically equivalent to the original, but standard in some sense . Semantic transformations use additional knowledge that the system owns, such as integrity constraints. As a result of semantic transformations, a query is obtained that is not syntactically equivalent to the original one, but gives the same result .

Step 3 (Generate query execution plans and select the optimal plan) . In this step, the optimizer generates a set of possible query execution plans. Each plan is constructed as a combination of low-level procedures for accessing data from tables, methods for joining tables. Of all the plans generated, a plan with the lowest cost is selected. At the same time, data on the presence of indexes on tables, statistical data on the distribution of values ​​in tables, etc. are analyzed. The cost of the plan is usually the sum of the costs of performing the individual low-level procedures that are used to carry it out. The cost of a separate procedure may include estimates of the number of accesses to the disks, the degree of processor utilization, and other parameters.

Step 4. (Execution of the request plan) . In this step, the plan selected in the previous step is transferred to the actual implementation.

In many ways, the quality of a particular DBMS is determined by the quality of its optimizer. A good optimizer can increase the speed of a query by several orders of magnitude. The quality of the optimizer is determined by what methods of transformation it can use, what statistical and other information about the tables it has, what methods for estimating the cost of executing the plan it knows.

Implementing relational algebra using the SELECT (SQL relational completeness) operator

In order to show that the SQL language is relationally complete, it is necessary to show that any relational operator can be expressed by means of SQL. In fact, it suffices to show that using SQL tools we can express any of the primitive relational operators.

Cartesian operator

Relational algebra: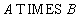

SQL statement:

  SELECT A.Pole1, A.Pole2, ..., B.Pole1, B.Pole2, ...
     FROM A, B;

or

  SELECT A.Pole1, A.Pole2, ..., B.Pole1, B.Pole2, ...
     FROM A CROSS JOIN B;

Projection operator

Relational algebra: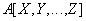

SQL statement:

  SELECT DISTINCT X, Y, ..., Z
     FROM A;

Sampling operator

Relational algebra: ,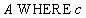

SQL statement:

  SELECT *
     FROM A
     WHERE c;

Union operator

Relational algebra: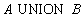

SQL statement:

  SELECT *
     FROM A
     UNION
     SELECT *
         FROM B;

Subtraction operator

Relational algebra: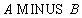

  SQL statement:
 SELECT *
     FROM A
     EXCEPT
     SELECT *
         FROM B

The relational rename operator RENAME is expressed using the AS keyword in the list of selectable fields of the SELECT statement. Thus, the SQL language is relationally complete.

The remaining operators of relational algebra (connection, intersection, division) are expressed in terms of primitive, therefore, can be expressed by SQL operators. However, for practical purposes we give them.

Connection operator

Relational algebra: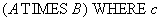

SQL statement:

  SELECT A.Pole1, A.Pole2, ..., B.Pole1, B.Pole2, ...
     FROM A, B
     WHERE c;

or

  SELECT A.Pole1, A.Pole2, ..., B.Pole1, B.Pole2, ...
     FROM A CROSS JOIN B
     WHERE c;

Intersection operator

Relational algebra: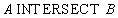

SQL statement:

  SELECT *
     FROM A
     INTERSECT
     SELECT *
         FROM B;

Division operator

Relational algebra: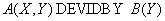

SQL statement:

  SELECT DISTINCT AX
   FROM A
   WHERE NOT EXIST
     (SELECT *
         FROM B
         WHERE NOT EXIST
           (SELECT *
               FROM A A1
               WHERE
                   A1.X = AX AND
                   A1.Y = BY));

Remark The SQL statement that implements the division of relationships is difficult to remember, so we give an example of an equivalent transformation of expressions representing the essence of the query.

Let relation A contain details of the supply of parts, relation B contains a list of all the parts that can be supplied. The attribute X is the supplier number, the attribute Y is the part number.

Splitting relationship A into relationship B means in this example, “select vendor numbers that supply all parts.”

Convert the text of the expression:

"Select vendor numbers that supply all parts" is equivalent to

"Select those supplier numbers from Table A for which there are no non-deliverable parts in Table B" is equivalent to

"Select those supplier numbers from table A for which there are no part numbers from table B that are not supplied by this supplier" is equivalent to

"Select those supplier numbers from Table A for which there are no parts numbers from Table B for which there are no supply records in Table A for this supplier and this part."

The last expression is literally translated into SQL. When translating an expression into the SQL language, it is necessary to take into account that in the internal subquery, table A must be renamed in order to distinguish it from the instance of the same table used in the external query.

findings

In fact, SQL (Structured Query Language) has now become the standard database access language.

The SQL language uses terms that are slightly different from the terms of the relational theory, for example, instead of "relations", "tables" are used, instead of "tuples" - "rows", instead of "attributes" - "columns" or "columns".

The standard of the SQL language, although it is based on the relational theory, but in many places it departs from it.

The basis of the SQL language is made up of operators that are conditionally divided into several groups of the functions they perform:

• DDL (Data Definition Language) operators are operators for defining database objects.
• DML (Data Manipulation Language) Operators are data manipulation statements.
• Security and data management operators, etc.

One of the main DML statements is the SELECT statement, which allows you to extract data from tables and receive answers to various queries. The SELECT statement contains all the capabilities of relational algebra. This means that any relational algebra operator can be expressed using the appropriate SELECT operator. This proves the relational completeness of the SQL language.

A distinction is made between the conceptual scheme for the execution of a SELECT statement and the actual scheme for its execution. A conceptual diagram describes the logical sequence in which operations must be performed in order to obtain a result. In the real execution of the SELECT statement, the achievement of the maximum speed of the query execution comes to the fore. To do this, use the optimizer , which, analyzing various plans for executing a query, selects the best among them.