Lecture
In the previous chapter, normal forms up to the third normal form (3NF) were considered. In most cases, this is quite enough to develop fully functional databases. This chapter discusses the normal forms of higher orders, namely, the normal form of Beuys-Codd (NFBK), the fourth normal form (4NF), the fifth normal form (5NF).
When reducing relations using the normalization algorithm to relations in 3NF, it was implicitly assumed that all relations contain one potential key. This is not always true. Consider the following example of a relationship containing two keys.
Example 1 Suppose you want to store data on the supply of parts of some suppliers. Suppose that supplier names are unique. In addition, each supplier has its own unique number. Supply data can be stored in the following respect:
| Vendor number PNUM | Supplier name PNAME | Detail number DNUM | Quantity supplied VOLUME |
|---|---|---|---|
| one | Firm 1 | one | 100 |
| one | Firm 1 | 2 | 200 |
| one | Firm 1 | 3 | 300 |
| 2 | Firm 2 | one | 150 |
| 2 | Firm 2 | 2 | 250 |
| 3 | Firm 3 | one | 1000 |
Table 1 Supply Relationship
This relationship contains two potential keys - { PNUM , DNUM } and { PNAME , DNUM } . It can be seen that the data is stored with respect to redundancy - when changing the name of the supplier, this name needs to be changed in all tuples where it occurs. Is it possible to eliminate this anomaly using the normalization algorithm described in the previous chapter? To do this, it is necessary to identify the existing functional dependencies (as usual, key attributes are italicized):
PNUM 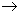 PNAME - the name of the supplier depends on the number of the supplier.
PNAME - the name of the supplier depends on the number of the supplier.
PNAME 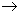 PNUM - supplier number depends on the name of the supplier.
PNUM - supplier number depends on the name of the supplier.
{ PNUM , DNUM } 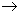 VOLUME - the quantity supplied depends on the first key of the relationship.
VOLUME - the quantity supplied depends on the first key of the relationship.
{ PNUM , DNUM } 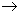 PNAME - supplier name depends on the first key of the relationship.
PNAME - supplier name depends on the first key of the relationship.
{ PNAME , DNUM } 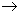 VOLUME - the quantity supplied depends on the second key of the relationship.
VOLUME - the quantity supplied depends on the second key of the relationship.
{ PNAME , DNUM } 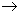 PNUM - supplier number depends on the second key of the relationship.
PNUM - supplier number depends on the second key of the relationship.
This relationship does not contain non-key attributes, depending on the part of the complex key (see definition 2NF). Indeed, the PNAME and PNUM attributes depend on the part of the complex key, but they themselves are key. Thus, the ratio is in 2NF.
In addition, the relation does not contain non-key attributes that are dependent on each other, since The only non-key attribute is VOLUME (see definition 3NF). Thus, it is shown that the “Supply” relationship is in 3NF.
Thus, the normalization algorithm described earlier is not applicable to this relation. It is obvious, however, that the anomaly of this relationship is eliminated by decomposing it into the following two relations:
| Vendor number PNUM | Supplier name PNAME |
|---|---|
| one | Firm 1 |
| 2 | Firm 2 |
| 3 | Firm 3 |
Table 2 Relationship "Suppliers"
| Vendor number PNUM | Detail number DNUM | Quantity supplied VOLUME |
|---|---|---|
| one | one | 100 |
| one | 2 | 200 |
| one | 3 | 300 |
| 2 | one | 150 |
| 2 | 2 | 250 |
| 3 | one | 1000 |
Table 3 Relationship "Supplies-2"
Definition 1 . Attitude  is in Boyce-Codd normal form ( NFBK ) if and only if the determinants of all functional dependencies are potential keys .
is in Boyce-Codd normal form ( NFBK ) if and only if the determinants of all functional dependencies are potential keys .
Remark If the relation is in the NFBK, then it is automatically located in 3NF. Indeed, this immediately follows from the definition of 3NF.
The “Delivery” relationship is not in the NFBC, since there are dependencies ( PNUM 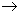 PNAME and PNAME
PNAME and PNAME 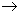 PNUM ) whose determinants are not potential keys.
PNUM ) whose determinants are not potential keys.
In order to eliminate dependence on determinants that are not potential keys, it is necessary to decompose, bringing these determinants and their dependent parts into a separate relation. Relationship "Suppliers" and "Deliveries-2", obtained as a result of decomposition are in the NFBK.
Remark The given decomposition of the “Supply” relationship into the “Supplier” and “Delivery-2” relations is not the only possible one. Alternative decomposition is decomposition into the following relations:
| Vendor number PNUM | Supplier name PNAME |
|---|---|
| one | Firm 1 |
| 2 | Firm 2 |
| 3 | Firm 3 |
Table 4 Relationship "Suppliers"
| Supplier name PNAME | Detail number DNUM | Quantity supplied VOLUME |
|---|---|---|
| Firm 1 | one | 100 |
| Firm 1 | 2 | 200 |
| Firm 1 | 3 | 300 |
| Firm 2 | one | 150 |
| Firm 2 | 2 | 250 |
| Firm 3 | one | 1000 |
Table 5 Supply-3 Relationship
At first glance, such a decomposition is worse than the first. Indeed, the names of suppliers are still repeated, and when changing the name of the supplier, this name will have to be changed simultaneously in several places (especially in two respects at once!). It seems that the situation has become even worse than it was before decomposition. However, this feeling arises from the fact that we intuitively believe that the names of suppliers can change, but the numbers - not. If we assume that supplier numbers can also change (why not - the director ordered suppliers to be renumbered!), Then the first decomposition turns out to be just as “bad” as the second - duplicate numbers will have to be changed simultaneously in several places and also in two ways at once.
In fact, there is no contradiction here. In the case of Supply-3, the Supplier Name attribute (PNAME) is the foreign key used to communicate with the Suppliers relationship. Therefore, when changing the supplier’s name, this change is made in relation to “Suppliers” and cascadingly (see the referential integrity strategies in Chapter 3) applies to the “Delivery-3” relationship in exactly the same way as changing the supplier’s number in a cascading relationship to -2 ". Therefore, formally both decompositions are completely equal. In real work, the developer chooses, of course, the first decomposition, but it is important to emphasize here that his choice is based entirely on other considerations that are not related to the formal theory of normal forms.
Remark The “Supply-2” relationship obtained as a result of decomposition has only one potential key . Therefore, to analyze the “Supply-2” relationship, it is not required to involve the definition of the NFBK, it is enough to define 3NF. Although the "Suppliers" relationship has two potential keys, but, since there are no other attributes in it; it is already so simply arranged that it cannot be simplified further. The question arises, are there any non-trivial examples of relations in the NFBK that are not in 3NF and are not as simple as the relationship "Suppliers"?
Example 2 Suppose that we still need to consider deliveries, but each delivery deed must have some unique number (let's call it “pass-through delivery number”). Attitude can be as follows:
| Vendor number PNUM | Detail number DNUM | Quantity supplied VOLUME | Pass-through delivery number Nn |
|---|---|---|---|
| one | one | 100 | one |
| one | 2 | 200 | 2 |
| one | 3 | 300 | 3 |
| 2 | one | 150 | four |
| 2 | 2 | 250 | five |
| 3 | one | 1000 | 6 |
Table 6 Relationship "Deliveries-with-number"
One potential key of this relationship is, as before, a pair of attributes { PNUM , DNUM } . Another key, due to the uniqueness of the pass-through number, is the NN attribute. In this respect, there are the following functional dependencies:
Attribute dependence on the first key of the relationship:
{ PNUM , DNUM } 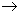 VOLUME ,
VOLUME ,
{ PNUM , DNUM } 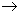 Nn
Nn
Attribute dependence on the second key of the relationship:
Nn 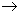 PNUM ,
PNUM ,
Nn 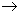 DNUM ,
DNUM ,
Nn 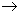 VOLUME ,
VOLUME ,
Dependencies resulting from dependencies on relation keys:
{ PNUM , DNUM } 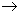 { VOLUME, NN } ,
{ VOLUME, NN } ,
Nn 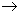 { PNUM , DNUM } ,
{ PNUM , DNUM } ,
Nn 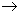 { PNUM , VOLUME} ,
{ PNUM , VOLUME} ,
Nn 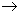 { DNUM , VOLUME} ,
{ DNUM , VOLUME} ,
Nn 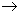 { PNUM , DNUM , VOLUME} .
{ PNUM , DNUM , VOLUME} .
As you can see, the determinants of all dependencies are potential keys, so this relationship is in the NFBK. A feature of this relationship is that it has two completely independent potential keys.
Consider the following example. Suppose you want to take into account data on applicants entering the university. When analyzing the subject area, the following requirements were identified:
Suppose that we need to store data about what items each entrant must pass. We will try to store data in one respect "Applicants-Faculties-Subjects":
| Enrollee | Faculty | Thing |
|---|---|---|
| Ivanov | Mathematical | Maths |
| Ivanov | Mathematical | Computer science |
| Ivanov | Physical | Maths |
| Ivanov | Physical | Physics |
| Petrov | Mathematical | Maths |
| Petrov | Mathematical | Computer science |
Table 7 Relationship "Applicants-Faculties-Objects"
At the moment, in relation to the stored information that the applicant Ivanov enters the two faculties (mathematically and physical), and the applicant Petrov - only in mathematics. In addition, it can be concluded that at the Faculty of Mathematics it is necessary to take mathematics and computer science, and on the physical - mathematics and physics.
It seems that in relation to there is an anomaly of the update, due to the fact that duplicates of the names of applicants, the names of faculties and the names of subjects are duplicated. However, this anomaly is easily eliminated in the standard way - by putting all the names into separate relations, leaving only the corresponding numbers in the original relation:
| room Entrant | room Faculty | room Subject |
|---|---|---|
| one | one | one |
| one | one | 2 |
| one | 2 | one |
| one | 2 | 3 |
| 2 | one | one |
| 2 | one | 2 |
Table 8 The modified relationship "Applicants-Faculties-Objects"
| room Entrant | Enrollee |
|---|---|
| one | Ivanov |
| 2 | Petrov |
Table 9 Attitude "Applicants"
| room Faculty | Faculty |
|---|---|
| one | Mathematical |
| 2 | Physical |
Table 10 Attitude "Faculties"
| room Subject | Thing |
|---|---|
| one | Maths |
| 2 | Computer science |
| 3 | Physics |
Table 11 Attitude "Objects"
Now each name is found only in one place.
And yet, both in the original and in the modified relation, there are update anomalies that occur when you try to insert or delete tuples.
Anomaly insertion . When trying to add a new tuple to the "Applicants-Faculties-Subjects" relation, for example (Sidorov, Mathematical, Mathematics), we must also add a tuple (Sidorov, Mathematical, Computer science), since All applicants of the Faculty of Mathematics are obliged to have the same list of donated items. Accordingly, when trying to insert a tuple (3, 1, 1) into a modified relation, we must also insert a tuple (3, 1, 2) into it.
Anomaly removal. When trying to remove a tuple (Ivanov, Mathematical, Mathematics), we must also remove the tuple (Ivanov, Mathematical, Computer science) for the same reason.
Thus, insertion and deletion of tuples cannot be performed independently of other relation tuples.
In addition, if we remove the tuple (Ivanov, Physical, Mathematics), and with it the tuple (Ivanov, Physical, Physics), then information will be lost about the subjects that should be surrendered at the physics department.
Decomposition of the "Applicants-Faculties-Subjects" relationship to eliminate the indicated anomalies cannot be performed on the basis of functional dependencies, since This relationship does not contain any functional dependencies . This relationship is completely key, i.e. the key of a relationship is the whole set of attributes. But it is clear that there is some kind of relationship between the attributes. This relationship is described by the concept of a multi-valued relationship .
Definition 2 . Let be  - attitude, and
- attitude, and 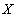 ,
, 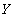 ,
, 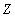 - some of its attributes (or disjoint attribute sets).
- some of its attributes (or disjoint attribute sets).
Then attributes (attribute sets) 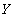 and
and 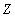 depend heavily on
depend heavily on 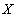 (denoted by
(denoted by 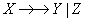 ), if and only if from the fact that with respect to
), if and only if from the fact that with respect to  contain tuples
contain tuples 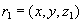 and
and 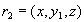 it follows that with respect
it follows that with respect  there is also a tuple to
there is also a tuple to 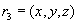 .
.
Remark Swapping tuples 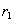 and
and 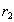 in the definition of a multi-valued relationship, we get that in relation to
in the definition of a multi-valued relationship, we get that in relation to  the tuple must also be contained
the tuple must also be contained 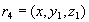 . So the attributes
. So the attributes 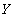 and
and 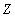 dependently on
dependently on 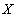 behave "symmetrically" with respect to the attribute
behave "symmetrically" with respect to the attribute 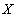 .
.
With regard to "Applicants-Faculties-Subjects" there is a significant relationship Faculty 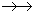 Entrant | Subject.
Entrant | Subject.
This can be expressed in words as follows - for each faculty (for each value from 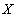 ) each applicant entering him (value from
) each applicant entering him (value from 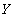 ) handles the same list of items (set of values from
) handles the same list of items (set of values from 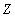 ), and for each faculty (for each value of
), and for each faculty (for each value of 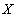 ) each pass on the faculty exam (the value of
) each pass on the faculty exam (the value of 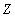 ) is submitted by the same list of applicants (a set of values from
) is submitted by the same list of applicants (a set of values from 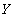 ). It is the presence of this dependency that does not allow for independently inserting and deleting tuples. Tuples are required to be inserted and removed simultaneously in whole sets .
). It is the presence of this dependency that does not allow for independently inserting and deleting tuples. Tuples are required to be inserted and removed simultaneously in whole sets .
Remark If regarding  there are at least three attributes
there are at least three attributes 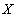 ,
, 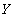 ,
, 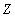 and there is a functional dependency
and there is a functional dependency 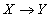 , that is, a multiple-valued dependence
, that is, a multiple-valued dependence 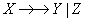 .
.
Indeed, acting formally in accordance with the definition of a multi-valued dependence, suppose that with respect to  contain tuples
contain tuples 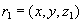 and
and 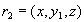 . Due to functional dependence
. Due to functional dependence 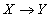 it follows that
it follows that 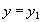 . But then the tuple
. But then the tuple 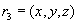 exactly the same as the tuple
exactly the same as the tuple 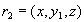 and therefore contained in relation
and therefore contained in relation  . Thus, there is a multi-valued relationship
. Thus, there is a multi-valued relationship 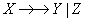 .
.
Thus, the concept of a multivalued dependence is a generalization of the concept of functional dependence .
Definition 3 . Many-valued dependency 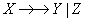 is called a non-trivial multivalued dependency , if there are no functional dependencies
is called a non-trivial multivalued dependency , if there are no functional dependencies 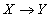 and
and 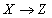 .
.
With regard to "Applicants-Faculties-Subjects" there is precisely a nontrivial multivalued dependence Faculty 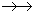 Entrant | Subject. Due to the nontriviality of this dependence, we cannot use the Hez theorem to decompose the relation. However, Fagin R. [52] proved the following theorem:
Entrant | Subject. Due to the nontriviality of this dependence, we cannot use the Hez theorem to decompose the relation. However, Fagin R. [52] proved the following theorem:
Theorem (Fagin) . Let be 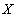 ,
, 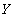 ,
, 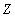 - disjoint sets of relation attributes
- disjoint sets of relation attributes 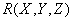 .
.
Relation decomposition  on the projection
on the projection 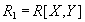 and
and 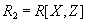 will be lossless decomposition if and only if there is a multi-valued relationship
will be lossless decomposition if and only if there is a multi-valued relationship 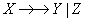 .
.
RemarkIf the dependency 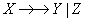 is trivial, i.e. there is one of the functional dependencies
is trivial, i.e. there is one of the functional dependencies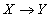 or
or 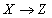 then we get the Hez theorem.
then we get the Hez theorem.
Proof of the theorem .
Necessity . Let decomposition of a relation on a projection
on a projection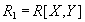 and
and 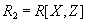 is lossless decomposition. Prove that
is lossless decomposition. Prove that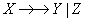 .
.
Suppose the relation  contains tuples
contains tuples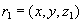 and
and 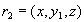 .It is necessary to prove that the tuple is
.It is necessary to prove that the tuple is 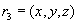 also contained in
also contained in .By the definition of projections, a tuple is
.By the definition of projections, a tuple is 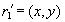 contained in
contained in 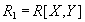 , and a tuple is
, and a tuple is 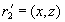 contained in
contained in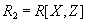 .Then the tuple is
.Then the tuple is 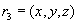 contained in the natural connection
contained in the natural connection 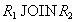 , and since decomposition is a lossless decomposition, this tuple is contained in
, and since decomposition is a lossless decomposition, this tuple is contained in . Necessity is proved .
. Necessity is proved .
Sufficiency . Let there be a multi-valued dependence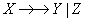 .Let us prove that the decomposition of a relation
.Let us prove that the decomposition of a relation  on a projection
on a projection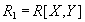 and
and 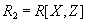 is lossless decomposition.
is lossless decomposition.
As in the proof of the Hez theorem, it is necessary to prove that 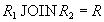 for any state of a relation
for any state of a relation .
.
The inclusion is 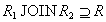 proved as in the Hez theorem. Such inclusion is always performed for any decomposition of a relation.
proved as in the Hez theorem. Such inclusion is always performed for any decomposition of a relation. .
.
We prove the inclusion 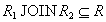 . Let the tuple
. Let the tuple 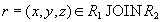 .This means that the projection
.This means that the projection 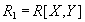 contains a tuple
contains a tuple 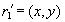 , and the projection
, and the projection 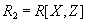 contains a tuple
contains a tuple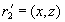 . По определению проекции, найдется такое значение
. По определению проекции, найдется такое значение 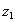 атрибута
атрибута 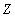 , что отношение
, что отношение  содержит кортеж
содержит кортеж 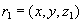 . Аналогично, найдется такое значение
. Аналогично, найдется такое значение 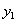 атрибута
атрибута 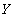 , что отношение
, что отношение  содержит кортеж
содержит кортеж 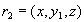 . Тогда по определению многозначной зависимости кортеж
. Тогда по определению многозначной зависимости кортеж 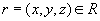 . Включение доказано. Достаточность доказана . Теорема доказана .
. Включение доказано. Достаточность доказана . Теорема доказана .
Определение 4 . Отношение  находится в четвертой нормальной форме ( 4НФ ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей .
находится в четвертой нормальной форме ( 4НФ ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей .
Отношение "Абитуриенты-Факультеты-Предметы" находится в НФБК, но не в 4НФ. Согласно теореме Фейджина, это отношение можно без потерь декомпозировать на отношения:
| Faculty | Абитуриент |
|---|---|
| Математический | Ivanov |
| Физический | Ivanov |
| Математический | Петров |
Таблица 12 Отношение "Факультеты-Абитуриенты"
| Faculty | Thing |
|---|---|
| Математический | Maths |
| Математический | Computer science |
| Физический | Maths |
| Физический | Physics |
Таблица 13 Отношение "Факультеты-Предметы"
В полученных отношениях устранены аномалии вставки и удаления, характерные для отношения "Абитуриенты-Факультеты-Предметы".
Заметим, что полученные отношения остались полностью ключевыми, и в них по-прежнему нет функциональных зависимостей.
Отношения с нетривиальными многозначными зависимостями возникают, как правило, в результате естественного соединения двух отношений по общему полю, которое не является ключевым ни в одном из отношений . Фактически это приводит к попытке хранить в одном отношении информацию о двух независимых сущностях. В качестве еще одного примера можно привести ситуацию, когда сотрудник может иметь много работ и много детей. Хранение информации о работах и детях в одном отношении приводит к возникновению нетривиальной многозначной зависимости Работник 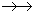 Работа|Дети.
Работа|Дети.
Функциональные и многозначные зависимости позволяют произвести декомпозицию исходного отношения без потерь на две проекции. Можно, однако, привести примеры отношений, которые нельзя декомпозировать без потерь ни на какие две проекции.
Example 3 Рассмотрим следующее отношение  :
:
| X | Y | Z |
|---|---|---|
| one | one | 2 |
| one | 2 | one |
| 2 | one | one |
| one | one | one |
Таблица 14 Отношение R
Всевозможные проекции отношения  , включающие по два атрибута, имеют вид:
, включающие по два атрибута, имеют вид:
| X | Y |
|---|---|
| one | one |
| one | 2 |
| 2 | one |
Таблица 15 Проекция R1=R[X,Y]
| X | Z |
|---|---|
| one | 2 |
| one | one |
| 2 | one |
Таблица 16 Проекция R2=R[X,Z]
| Y | Z |
|---|---|
| one | 2 |
| 2 | one |
| one | one |
Таблица 17 Проекция R3=R[Y,Z]
Как легко заметить, отношение  не восстанавливается ни по одному из попарных соединений
не восстанавливается ни по одному из попарных соединений 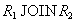 ,
, 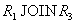 or
or 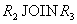 . Действительно, соединение
. Действительно, соединение 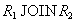 имеет вид:
имеет вид:
| X | Y | Z |
|---|---|---|
| one | one | 2 |
| one | one | one |
| one | 2 | 2 |
| one | 2 | one |
| 2 | one | one |
Таблица 18 R1 JOIN R2
Серым цветом выделен лишний кортеж, отсутствующий в отношении  . Аналогично (в силу соображений симметрии) и другие попарные соединения не восстанавливают отношения
. Аналогично (в силу соображений симметрии) и другие попарные соединения не восстанавливают отношения  .
.
Однако отношение  восстанавливается соединением всех трех проекций:
восстанавливается соединением всех трех проекций:
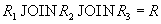 .
.
Это говорит о том, что между атрибутами этого отношения также имеется некоторая зависимость, но эта зависимость не является ни функциональной, ни многозначной зависимостью.
Определение 5 . Let be  является отношением, а
является отношением, а 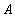 ,
, 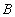 , ...,
, ..., 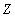 - произвольными (возможно пересекающимися) подмножествами множества атрибутов отношения
- произвольными (возможно пересекающимися) подмножествами множества атрибутов отношения  . Тогда отношение
. Тогда отношение  удовлетворяет зависимости соединения
удовлетворяет зависимости соединения
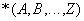
тогда и только тогда, когда оно равносильно соединению всех своих проекций с подмножествами атрибутов 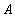 ,
, 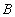 , ...,
, ..., 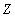 i.e.
i.e.
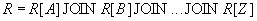 .
.
Можно предположить , что отношение  в примере 3 удовлетворяет следующей зависимости соединения:
в примере 3 удовлетворяет следующей зависимости соединения:
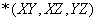 .
.
Утверждать, что это именно так мы пока не можем, т.к. определение зависимости соединения должно выполняться для любого состояния отношения  , а не только для состояния, приведенного в примере.
, а не только для состояния, приведенного в примере.
Покажем, что зависимость соединения является обобщением понятия многозначной зависимости. Действительно, согласно теореме Фейджина, отношение 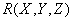 может быть декомпозировано без потерь на проекции
может быть декомпозировано без потерь на проекции 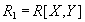 and
and 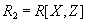 тогда и только тогда, когда имеется многозначная зависимость
тогда и только тогда, когда имеется многозначная зависимость 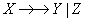 . Согласно определению зависимости соединения, теорема Фейджина может быть переформулирована следующим образом:
. Согласно определению зависимости соединения, теорема Фейджина может быть переформулирована следующим образом:
Теорема Фейджина (другая формулировка) . Отношение 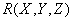 удовлетворяет зависимости соединения
удовлетворяет зависимости соединения 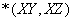 тогда и только тогда, когда имеется многозначная зависимость
тогда и только тогда, когда имеется многозначная зависимость 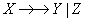 .
.
Because теорема Фейджина является взаимно обратной, то ее можно взять в качестве определения многозначной зависимости. Таким образом, многозначная зависимость является частным случаем зависимости соединения, т.е., если в отношении имеется многозначная зависимость, то имеется и зависимость соединения. Обратное, конечно, неверно.
Определение 6 . Зависимость соединения 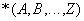 называется нетривиальной зависимостью соединения , если выполняется два условия:
называется нетривиальной зависимостью соединения , если выполняется два условия:
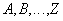 не содержит потенциального ключа отношения
не содержит потенциального ключа отношения  .
.  .
. Для удобства работы сформулируем это определение так же и в отрицательной форме:
Определение 7 . Зависимость соединения 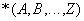 называется тривиальной зависимостью соединения , если выполняется одно из условий:
называется тривиальной зависимостью соединения , если выполняется одно из условий:
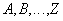 содержат потенциальный ключ отношения
содержат потенциальный ключ отношения  .
.  .
. Определение 8 . Отношение  находится в пятой нормальной форме ( 5НФ ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной .
находится в пятой нормальной форме ( 5НФ ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной .
Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:
Определение 9 . Отношение  не находится в 5НФ , если в отношении найдется нетривиальная зависимость соединения .
не находится в 5НФ , если в отношении найдется нетривиальная зависимость соединения .
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении  :
:
(i) Отношение  является полностью ключевым (т.е. потенциальным ключом отношения является все множество атрибутов).
является полностью ключевым (т.е. потенциальным ключом отношения является все множество атрибутов).
(ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении  содержатся кортежи
содержатся кортежи 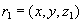 ,
, 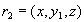 and
and 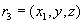 , то отсюда следует, что в отношении
, то отсюда следует, что в отношении  содержится также и кортеж
содержится также и кортеж 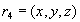 .
.
Утверждение . Докажем, что при наличии ограничений (i) и (ii), отношение находится в 4НФ, но не в 5НФ.
Доказательство . Покажем, что отношение  находится в 4НФ. Согласно определению 4НФ, необходимо показать, что отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей. Because отношение является полностью ключевым, то оно автоматически находится в НФБК. Если бы в отношении имелась многозначная зависимость (необязательно нетривиальная), то, согласно теореме Фейджина, отношение можно было бы декомпозировать без потерь на две проекции. Но пример 3 показывает, что таких декомпозиций нет (здесь мы воспользовались тем, что для доказательства возможности декомпозиции необходимо доказать ее для всех возможных состояний отношения, а для доказательства невозможности достаточно привести один контрпример). Поэтому в отношении нет никаких многозначных зависимостей.
находится в 4НФ. Согласно определению 4НФ, необходимо показать, что отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей. Because отношение является полностью ключевым, то оно автоматически находится в НФБК. Если бы в отношении имелась многозначная зависимость (необязательно нетривиальная), то, согласно теореме Фейджина, отношение можно было бы декомпозировать без потерь на две проекции. Но пример 3 показывает, что таких декомпозиций нет (здесь мы воспользовались тем, что для доказательства возможности декомпозиции необходимо доказать ее для всех возможных состояний отношения, а для доказательства невозможности достаточно привести один контрпример). Поэтому в отношении нет никаких многозначных зависимостей.
Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является 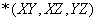 . Если это действительно зависимость соединения, то она нетривиальна. Действительно, ни одно из множеств атрибутов
. Если это действительно зависимость соединения, то она нетривиальна. Действительно, ни одно из множеств атрибутов 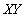 ,
, 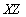 and
and 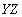 не совпадает с множеством всех атрибутов отношения
не совпадает с множеством всех атрибутов отношения  и не содержит потенциального ключа.
и не содержит потенциального ключа.
Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции 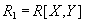 ,
, 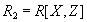 and
and 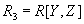 является декомпозицией без потерь для любого состояния отношения
является декомпозицией без потерь для любого состояния отношения  (именно здесь содержится ключевая тонкость, обычно пропускаемая при анализе конкретного состояния отношения
(именно здесь содержится ключевая тонкость, обычно пропускаемая при анализе конкретного состояния отношения  в примере 3, и именно здесь нам понадобятся знания о предметной области, выраженные в утверждении (ii)).
в примере 3, и именно здесь нам понадобятся знания о предметной области, выраженные в утверждении (ii)).
Как и в предыдущих доказательствах, нужно доказать, что 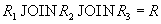 для любого состояния отношения
для любого состояния отношения  .
.
Включение 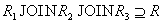 доказывается как в теореме Хеза. Такое включение выполняется всегда для любой декомпозиции отношения
доказывается как в теореме Хеза. Такое включение выполняется всегда для любой декомпозиции отношения  .
.
Докажем включение 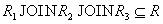 .
.
Пусть кортеж  . Это означает, что в проекции
. Это означает, что в проекции 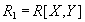 содержится кортеж
содержится кортеж 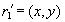 , в проекции
, в проекции 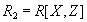 содержится кортеж
содержится кортеж 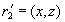 , а в проекции
, а в проекции 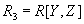 содержится кортеж
содержится кортеж 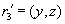 . По определению проекции, найдутся такие значения
. По определению проекции, найдутся такие значения 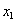 ,
, 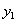 ,
, 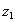 атрибутов
атрибутов 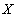 ,
, 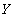 and
and 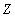 соответственно, что отношение
соответственно, что отношение  содержит кортежи
содержит кортежи 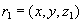 ,
, 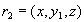 and
and 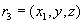 . Но тогда по условию (ii) в отношении
. Но тогда по условию (ii) в отношении  содержится также и кортеж
содержится также и кортеж 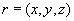 . Этим доказано необходимое включение. Утверждение доказано .
. Этим доказано необходимое включение. Утверждение доказано .
В предыдущей главе был описан алгоритм нормализации как алгоритм приведения отношений к 3НФ. Теперь мы можем продолжить этот алгоритм, доведя его до алгоритма приведения к 5НФ.
Шаг 4 (Приведение к НФБК) . Если имеются отношения, содержащие несколько потенциальных ключей, то необходимо проверить, имеются ли функциональные зависимости, детерминанты которых не являются потенциальными ключами. Если такие функциональные зависимости имеются, то необходимо провести дальнейшую декомпозицию отношений. Те атрибуты, которые зависят от детерминантов, не являющихся потенциальными ключами выносятся в отдельное отношение вместе с детерминантами.
Шаг 5 (Приведение к 4НФ) . Если в отношениях обнаружены нетривиальные многозначные зависимости, то необходимо провести декомпозицию для исключения таких зависимостей.
Шаг 5 (Приведение к 5НФ) . Если в отношениях обнаружены нетривиальные зависимости соединения, то необходимо провести декомпозицию для исключения и таких зависимостей.
Обобщением 3НФ на случай, когда отношение имеет более одного потенциального ключа, является нормальная форма Бойса-Кодда.
Отношение  находится в нормальной форме Бойса-Кодда ( НФБК ) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
находится в нормальной форме Бойса-Кодда ( НФБК ) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
Нормализация отношений вплоть до нормальной формы Бойса-Кодда основывалась на понятии функциональной зависимости и теореме Хеза, гарантировавшей, что декомпозиция будет происходить без потерь информации.
Дальнейшая нормализация связана уже с обобщением понятия функциональной зависимости.
Атрибуты (множества атрибутов) 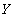 and
and 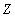 многозначно зависят от
многозначно зависят от 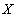 , (
, ( 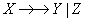 ), тогда и только тогда, когда из того, что в отношении
), тогда и только тогда, когда из того, что в отношении  содержатся кортежи
содержатся кортежи 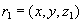 and
and 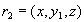 следует, что в отношении
следует, что в отношении  содержится также и кортеж к
содержится также и кортеж к 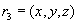 .
.
Корректность дальнейшей декомпозиции основывается на теореме Фейджина, которая говорит о том, что декомпозиция отношения на две проекции является декомпозицией без потерь тогда и только тогда, когда в отношении имеется некоторая многозначная зависимость.
Если в отношении имеется функциональная зависимость, то автоматически имеется и тривиальная многозначная зависимость, определяемая этой функциональной зависимостью.
Многозначная зависимость 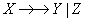 называется нетривиальной многозначной зависимостью , если не существует функциональных зависимостей
называется нетривиальной многозначной зависимостью , если не существует функциональных зависимостей 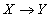 and
and 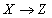 .
.
Отношение  находится в четвертой нормальной форме ( 4НФ ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
находится в четвертой нормальной форме ( 4НФ ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
Имеют место зависимости специального вида, когда отношение не может быть подвергнуто декомпозиции без потерь на две проекции, но может быть декомпозировано на большее число проекций. Такие зависимости называются зависимостями соединения и являются обобщением понятия многозначной зависимости.
A relation  is in the fifth normal form ( 5NF ) if and only if any existing dependence of the compound is trivial .
is in the fifth normal form ( 5NF ) if and only if any existing dependence of the compound is trivial .
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL