Lecture
The simplest data structure used in mathematics occurs when there are no interconnections between individual isolated data. The combination of such data is a set . The concept of a set is an undefined concept. The set does not have an internal structure. A set can be imagined as a collection of elements with some common property. In order for some set of elements to be called a set, it is necessary that the following conditions be fulfilled:
Sets are usually denoted by capital Latin letters. If the item 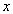 belongs to many
belongs to many 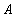 then it is denoted by:
then it is denoted by:
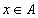
If each element of the set 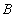 is also an element of the set
is also an element of the set 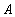 then they say that a lot
then they say that a lot 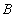 is a subset of the set
is a subset of the set 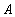 :
:
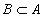
Subset 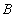 sets
sets 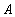 called its own subset if
called its own subset if
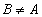
Using the concept of a set, one can construct more complex and informative objects.
The main operations on sets are union , intersection, and difference .
Definition 1 . The union of two sets is a new set.

Definition 2 . The intersection of two sets is a new set.

Definition 3 . The difference of two sets is a new set.
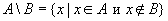
If the class of objects on which different sets are defined denote 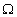 ( Universum ), then the complement of the set
( Universum ), then the complement of the set 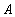 call the difference
call the difference
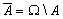
One of the ways to construct new objects from the already existing sets is the Cartesian product of sets .
Let be 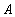 and
and 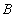 - sets. Expression type
- sets. Expression type 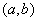 where
where 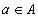 and
and 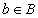 is called an ordered pair . Equality of the form
is called an ordered pair . Equality of the form 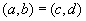 means that
means that 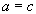 and
and 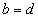 . In general, you can consider ordered n-ku
. In general, you can consider ordered n-ku 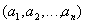 of the elements
of the elements 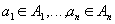 . Ordered n-ki otherwise called sets or tuples .
. Ordered n-ki otherwise called sets or tuples .
Definition 4 . Cartesian (direct) product of sets 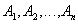 is called the set of ordered n-ok (sets, tuples) of the form
is called the set of ordered n-ok (sets, tuples) of the form
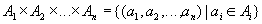
Definition 5 . Cartesian degree 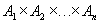 is called the number of sets n included in this Cartesian product.
is called the number of sets n included in this Cartesian product.
Remark If all the sets 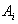 are the same then use the designation
are the same then use the designation
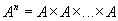 .
.
Definition 6 . Subset 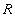 Cartesian product of sets
Cartesian product of sets 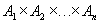 called the ratio of degree n ( n-ary ratio ).
called the ratio of degree n ( n-ary ratio ).
Definition 7 . The power of a set of tuples related to 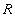 is called the ratio power
is called the ratio power 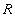 .
.
Remark The concept of relationship is very important not only from a mathematical point of view. The concept of relationship actually underlies the entire relational theory of databases. As will be shown below, relations are the mathematical analogue of tables . The term "relational data representation", first introduced by Codd [43], comes from the term relation , which is understood precisely in the sense of this definition.
Because Any set can be considered as a Cartesian product of degree 1, then any subset, like any set, can be considered a ratio of degree 1. This is not a very interesting example, indicating only that the terms "ratio of degree 1" and "subset" are synonymous. The nontriviality of the concept of a relationship is manifested when the degree of a relationship is greater than 1. Two points are key here:
First , all the elements of a relationship are of the same type of tuples. Tuples of the same type make it possible to consider them as analogs of rows in a simple table, i.e. in such a table, in which all rows consist of the same number of cells and the corresponding cells contain the same data types. For example, the relation consisting of the following three tuples {(1, "Ivanov", 1000), (2, "Petrov", 2000), (3, "Sidorov", 3000)} can be considered a table containing information about employees and their salaries. Such a table will have three rows and three columns, with each column containing data of the same type.
In contrast, consider the set {(1), (1, 2), (1, 2, 3)}, consisting of different types of numerical tuples. This set is not a relation to 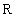 nor in
nor in 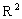 nor in
nor in 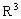 . From the tuples belonging to this set it is impossible to make a simple table. However, this set can be considered a ratio of degree 1 on the set of all possible numerical tuples of all possible degrees
. From the tuples belonging to this set it is impossible to make a simple table. However, this set can be considered a ratio of degree 1 on the set of all possible numerical tuples of all possible degrees 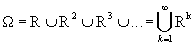 , but such an interpretation gives nothing new in comparison with the notion of a subset.
, but such an interpretation gives nothing new in comparison with the notion of a subset.
Secondly . Except in the extreme case when the relation is the Cartesian product itself. 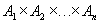 The relation does not include all possible tuples from the Cartesian product. This means that for each relationship there is a criterion that allows you to determine which tuples are related and which ones are not. This criterion, in essence, determines for us the meaning (semantics) of the relationship.
The relation does not include all possible tuples from the Cartesian product. This means that for each relationship there is a criterion that allows you to determine which tuples are related and which ones are not. This criterion, in essence, determines for us the meaning (semantics) of the relationship.
Indeed, each relation can be associated with a certain logical expression. 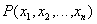 depending on n parameters (n-place predicate) and determining whether a tuple will be
depending on n parameters (n-place predicate) and determining whether a tuple will be 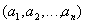 belong to a relation
belong to a relation 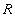 . This logical expression is called the relationship predicate.
. This logical expression is called the relationship predicate. 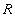 . More precisely, the tuple
. More precisely, the tuple 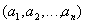 belongs to the relation
belongs to the relation 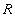 if and only if the predicate of this relationship
if and only if the predicate of this relationship 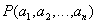 takes the value "true". In turn, each n-local predicate gives some n-ary relation. Thus, there is a one-to-one correspondence between n-ary relations and n-local predicates.
takes the value "true". In turn, each n-local predicate gives some n-ary relation. Thus, there is a one-to-one correspondence between n-ary relations and n-local predicates.
If it does not cause confusion, it is convenient and the relationship, and its predicate denoted by the same letter. For example, the ratio 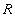 has a predicate
has a predicate 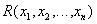 .
.
In mathematics, binary relations play an important role, i.e. relations defined on the Cartesian product of two sets 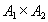 .
.
Definition 8 . Attitude 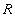 on set
on set 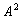 is called an equivalence relation if it has the following properties:
is called an equivalence relation if it has the following properties:
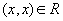 for all
for all 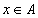 (reflexivity)
(reflexivity) 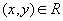 then
then 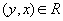 (symmetry)
(symmetry) 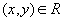 and
and 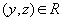 then
then 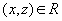 (transitivity)
(transitivity) Usually the equivalence relation is denoted by 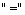 or
or 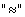 and they say that it (the relation) is given on the set
and they say that it (the relation) is given on the set 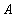 (and not on
(and not on 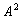 ). Conditions 1-3 in such designations look more natural:
). Conditions 1-3 in such designations look more natural:
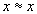 for all
for all 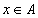 (reflexivity)
(reflexivity) 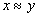 then
then 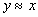 (symmetry)
(symmetry) 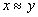 and
and 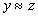 then
then 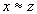 (transitivity)
(transitivity) It is easy to prove that if on the set 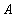 given an equivalence relation, then the set
given an equivalence relation, then the set 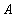 divided into mutually disjoint subsets consisting of equivalent elements ( equivalence classes ).
divided into mutually disjoint subsets consisting of equivalent elements ( equivalence classes ).
Example 1 Consider on the set of real numbers 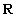 a relation defined simply by equality of numbers. The predicate of this relationship is:
a relation defined simply by equality of numbers. The predicate of this relationship is:
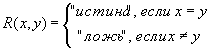 , or simply
, or simply 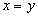
Conditions 1-3 are obviously satisfied, therefore this relation is an equivalence relation. Each equivalence class of this relation consists of one number.
Example 2 Consider a more complex equivalence relation. On the set of integers 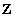 set the relationship "equality modulo n" as follows: two numbers
set the relationship "equality modulo n" as follows: two numbers 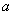 and
and 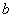 equal modulo n if their residues when divided by n are equal. For example, modulo 5 equals numbers 2, 7, 12, etc.
equal modulo n if their residues when divided by n are equal. For example, modulo 5 equals numbers 2, 7, 12, etc.
Conditions 1–3 are easily verified; therefore, modulo equality is an equivalence relation. The predicate of this relationship is:

The equivalence classes of this relation are made up of numbers that give the same residues when divided by n. There are exactly n such classes:
[0] = {0, n, 2n, ...}
[1] = {1, n + 1, 2n + 1, ...}
...
[n-1] = {n-1, n + n-1, 2n + n-1, ...}
Definition 9 . Attitude 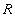 on set
on set 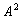 is called an order relation if it has the following properties:
is called an order relation if it has the following properties:
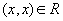 for all
for all 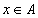 (reflexivity)
(reflexivity) 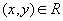 and
and 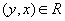 then
then 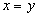 (antisymmetry)
(antisymmetry) 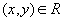 and
and 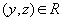 then
then 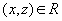 (transitivity)
(transitivity) Usually the order relationship is indicated by 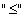 . If for two elements
. If for two elements 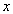 and
and 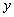 performed
performed 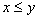 then say that
then say that 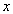 "preceded"
"preceded" 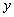 . As for the equivalence relation, conditions 1-3 in such notation look more natural:
. As for the equivalence relation, conditions 1-3 in such notation look more natural:
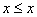 for all
for all 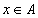 (reflexivity)
(reflexivity) 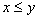 and
and 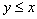 then
then 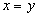 (antisymmetry)
(antisymmetry) 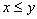 and
and 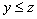 then
then 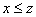 (transitivity)
(transitivity) Example 3 A simple example of an order relation is the relation given by the usual inequality 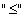 on the set of real numbers
on the set of real numbers 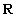 . Note that for any numbers
. Note that for any numbers 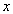 and
and 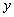 performed either
performed either 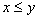 either
either 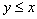 i.e. any two numbers are comparable. Such relationships are called full order relationships .
i.e. any two numbers are comparable. Such relationships are called full order relationships .
The predicate of this relationship is simply a statement. 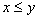 .
.
Пример 4 . Рассмотрим на множестве 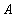 всех сотрудников некоторого предприятия отношение, задаваемое следующим образом: сотрудник
всех сотрудников некоторого предприятия отношение, задаваемое следующим образом: сотрудник 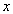 предшествует сотруднику
предшествует сотруднику 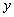 тогда и только тогда, когда выполняется одно из условий:
тогда и только тогда, когда выполняется одно из условий:
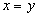
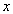 является начальником (не обязательно непосредственным)
является начальником (не обязательно непосредственным) 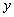
Назовем такое отношение "быть начальником". Легко проверить, что отношение "быть начальником" является отношением порядка. Заметим, что в отличие от предыдущего примера, существуют такие пары сотрудников 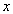 and
and 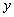 , для которых не выполняется ни
, для которых не выполняется ни 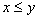 , ни
, ни 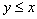 (for example, if
(for example, if 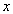 and
and 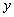 являются сослуживцами). Такие отношения, в которых есть несравнимые между собой элементы, называют отношениями частичного порядка .
являются сослуживцами). Такие отношения, в которых есть несравнимые между собой элементы, называют отношениями частичного порядка .
Определение 10 . Отношение 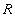 на декартовом произведении двух множеств
на декартовом произведении двух множеств 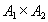 называется функциональным отношением , если оно обладает следующим свойством:
называется функциональным отношением , если оно обладает следующим свойством:
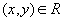 and
and 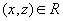 then
then 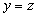 (однозначность функции).
(однозначность функции). Обычно, функциональное отношение обозначают в виде функциональной зависимости - 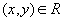 then and only if
then and only if 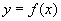 . Функциональные отношения (подмножества декартового произведения!) называют иначе графиком функции или графиком функциональной зависимости .
. Функциональные отношения (подмножества декартового произведения!) называют иначе графиком функции или графиком функциональной зависимости .
Предикат функционального отношения есть просто выражение функциональной зависимости 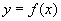 .
.
Пример 5 . Пусть множество 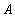 есть следующее множество молодых людей: {Вовочка, Петя, Маша, Лена}, причем известны следующие факты:
есть следующее множество молодых людей: {Вовочка, Петя, Маша, Лена}, причем известны следующие факты:
Information about the relationship of these young people can be described by the binary "love" relationship given on the set 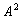 . This relationship can be described in several ways.
. This relationship can be described in several ways.
Method 1. Enumeration of facts in the form of an arbitrary text (as was done above).
Method 2. In the form of a relationship graph:
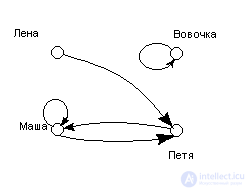
Figure 1 Relationship Graph
Method 3. Using the relationship matrix:
Whom Who | Little Johnny | Petya | Masha | Lena |
|---|---|---|---|---|
Little Johnny | Loves | |||
Petya | Loves | |||
Masha | Loves | Loves | ||
Lena | Loves |
Table 1. Relationship Matrix
Method 4. Using the fact table:
| Who loves | Who love |
|---|---|
| Little Johnny | Little Johnny |
| Petya | Masha |
| Masha | Petya |
| Masha | Masha |
| Lena | Petya |
Table 2 Fact Table
From the point of view of relational databases, the fourth method is most preferable, since it allows the most convenient way to store and manipulate information. Indeed, the enumeration of facts as a textual form of information storage is appropriate for a literary work, but it is difficult to process it algorithmatically. The image in the form of a graph is visual, and it is convenient to use it as the final form of presenting information to the user, but it is inconvenient to store data in a graphical form. The relationship matrix is more in line with the requirements of the information system. The matrix is convenient in processing and compactly stored. But one small change, for example, Vasya appeared and fell in love with unfortunate Lena, requires restructuring of the whole matrix, namely, adding both columns and columns. . Таблица фактов свободна от всех этих недостатков - при добавлении новых действующих лиц просто добавляются новые строки.
Что касается предиката данного отношения, то он имеет следующий вид (дизъюнктивная нормальная форма):
R(x,y) = {(x = "Вовочка" AND y = "Вовочка") OR (x = "Петя" AND y = "Маша") OR (x = "Маша" AND y = "Петя") OR (x = "Маша" AND y = "Маша") OR (x = "Лена" AND y = "Петя")}
Замечание. Приведенное отношение не является ни транзитивным, ни симметричным или антисимметричным, ни рефлексивным, поэтому оно не является ни отношением эквивалентности, ни отношением порядка, ни каким-либо другим разумным отношением.
Comment. Most of the world literature exists and makes sense only insofar as the binary relation "to love" is not an equivalence relation. In particular, for this reason, humanity is not divided into equivalence classes of mutually loving individuals. The study of the characteristics of this relationship and the corresponding predicate was engaged in (and continues to be engaged) by a large number of experts, such as Tolstoy L.N., Shakespeare V. and others.
In mathematics, n-ary relations are considered relatively rarely, unlike databases, where the most important are the relations defined on the Cartesian product of more than two sets .
Example 6 . At a university at the Faculty of Mathematics students are students Ivanov, Petrov and Sidorov. Lectures are given to them by the teachers of Pushkins, Tsyganov and Sharipov, and the following facts are known:
Для того чтобы формально описать данную ситуацию (например, в целях разработки информационной системы, учитывающей данные о ходе учебного процесса), введем три множества:
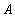 = {Пушников, Цыганов, Шарипов}.
= {Пушников, Цыганов, Шарипов}. 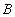 = {Алгебра, Геометрия, Базы данных}.
= {Алгебра, Геометрия, Базы данных}. 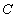 = {Иванов, Петров, Сидоров}.
= {Иванов, Петров, Сидоров}. Имеющиеся факты можно разделить на две группы. 1 группа (факты 1-3) - факты о преподавателях, 2 группа (факты 4-6) - факты о студентах.
Для того чтобы отразить факты 1-3 (характеризующие преподавателей и читаемые ими лекции), введем отношение 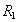 на декартовом произведении
на декартовом произведении 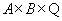 where
where 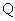 - множество рациональных чисел. А именно, упорядоченная тройка
- множество рациональных чисел. А именно, упорядоченная тройка 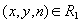 тогда и только тогда, когда преподаватель
тогда и только тогда, когда преподаватель 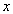 читает лекции по предмету
читает лекции по предмету 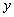 в количестве
в количестве 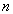 часов в семестр. Назовем такое отношение "Читает лекции по…". Множество кортежей, образующих отношение
часов в семестр. Назовем такое отношение "Читает лекции по…". Множество кортежей, образующих отношение 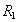 удобно представить в виде таблицы:
удобно представить в виде таблицы:
| A (Преподаватель) | B (Предмет) | Q (Количество часов) |
|---|---|---|
| Пушников | Algebra | 40 |
| Пушников | Базы данных | 80 |
| Цыганов | Geometry | 50 |
| Шарипов | Algebra | 40 |
| Шарипов | Geometry | 50 |
Таблица 3 Отношение "Читает лекции по…"
Для того чтобы отразить факты 4-6 (характеризующие посещение студентами лекций), введем отношение 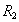 на декартовом произведении
на декартовом произведении 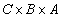 . Упорядоченная тройка
. Упорядоченная тройка 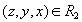 тогда и только тогда, когда студент
тогда и только тогда, когда студент 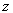 посещает лекции по предмету
посещает лекции по предмету 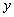 у преподавателя
у преподавателя 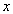 . Назовем это отношение "Посещать лекции". Его также представим в виде таблицы:
. Назовем это отношение "Посещать лекции". Его также представим в виде таблицы:
| C (студент) | B (предмет) | A (Преподаватель) |
|---|---|---|
| Ivanov | Algebra | Шарипов |
| Ivanov | Базы данных | Пушников |
| Петров | Algebra | Пушников |
| Петров | Geometry | Цыганов |
| Сидоров | Geometry | Цыганов |
| Сидоров | Базы данных | Пушников |
Таблица 4 Отношение "Посещать лекции"
Рассмотрим отношение 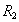 подробнее. Оно задано на декартовом произведении
подробнее. Оно задано на декартовом произведении 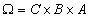 . Это произведение, содержащее 3*3*3=27 кортежей, можно назвать "Студенты-Лекции-Преподаватели". Множество
. Это произведение, содержащее 3*3*3=27 кортежей, можно назвать "Студенты-Лекции-Преподаватели". Множество 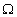 представляет собой совокупность всех возможных вариантов посещения студентами лекций. Отношение же
представляет собой совокупность всех возможных вариантов посещения студентами лекций. Отношение же 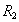 показывает текущее состояние учебного процесса. Очевидно, что отношение
показывает текущее состояние учебного процесса. Очевидно, что отношение 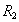 является изменяемым во времени отношением.
является изменяемым во времени отношением.
Итак, факты о ходе учебного процесса удалось отразить в виде двух отношений третьей степени (3-арных), а сами отношения изобразить в виде таблиц с тремя колонками.
Удобство использования табличной формы для задания отношения определяется в данном случае следующими факторами:
Нас сейчас не интересует вопрос, хороши ли полученные отношения. Заметим пока только, что, как показывают следующие замечания, не любую строку можно добавить в таблицу "Посещать лекции".
Remark В таблицу "Посещать лекции" нельзя добавить две одинаковые строки, т.к. таблица изображает отношение 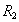 , а в отношении (как и в любом множестве) не может быть двух одинаковых элементов . Это пример синтаксического ограничения - такое ограничение задано в определении понятия отношение (одинаковых строк не может быть ни в одной таблице , задающей отношение).
, а в отношении (как и в любом множестве) не может быть двух одинаковых элементов . Это пример синтаксического ограничения - такое ограничение задано в определении понятия отношение (одинаковых строк не может быть ни в одной таблице , задающей отношение).
Remark В таблицу "Посещать лекции" нельзя добавить кортеж (Иванов, Геометрия, Пушников). Действительно, из таблицы "Читает лекции по…", представляющей отношение 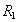 , следует, что Пушников не читает предмет "Геометрия". Оказалось, что таблицы связаны друг с другом, и существенным образом! Это пример семантического ограничения - такое ограничение является следствием нашей трактовки данных, хранящихся в отношении (следствием понимания смысла данных).
, следует, что Пушников не читает предмет "Геометрия". Оказалось, что таблицы связаны друг с другом, и существенным образом! Это пример семантического ограничения - такое ограничение является следствием нашей трактовки данных, хранящихся в отношении (следствием понимания смысла данных).
Введем понятие транзитивного замыкания , связанное с бинарными отношениями, которое понадобится в дальнейшем.
Определение 11. Пусть отношение 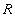 задано на декартовом квадрате
задано на декартовом квадрате 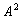 некоторого множества
некоторого множества 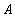 . Транзитивным замыканием отношения
. Транзитивным замыканием отношения 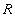 называется новое отношение
называется новое отношение 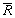 , состоящее из кортежей
, состоящее из кортежей 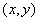 , для которых выполняется:
, для которых выполняется:
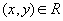 ,
, 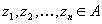 , такая, что все кортежи
, такая, что все кортежи 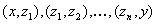 принадлежат отношению
принадлежат отношению 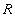 .
. It's obvious that 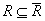 .
.
Пример 7 . Пусть множество 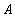 представляет собой следующее множество деталей и конструкций:
представляет собой следующее множество деталей и конструкций:
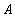 = {Болт, Гайка, Двигатель, Автомобиль, Колесо, Ось}
= {Болт, Гайка, Двигатель, Автомобиль, Колесо, Ось}
причем некоторые из деталей и конструкций могут использоваться при сборке других конструкций. Взаимосвязь деталей описывается отношением 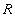 ("непосредственно используется в") и состоит из следующих кортежей:
("непосредственно используется в") и состоит из следующих кортежей:
| Design | Где используется |
|---|---|
| Болт | Engine |
| Болт | Колесо |
| Nut | Engine |
| Nut | Колесо |
| Engine | Car |
| Колесо | Car |
| Axis | Колесо |
Таблица 5 Отношение R
Транзитивное замыкание 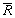 состоит из кортежей (добавленные кортежи помечены серым цветом):
состоит из кортежей (добавленные кортежи помечены серым цветом):
| Design | Где используется |
|---|---|
| Болт | Engine |
| Болт | Колесо |
| Nut | Engine |
| Nut | Колесо |
| Engine | Car |
| Колесо | Car |
| Axis | Колесо |
| Болт | Car |
| Nut | Car |
| Axis | Car |
Таблица 6 Транзитивное замыкание отношения R
Очевидный смысл замыкания 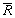 состоит в описании включения деталей друг в друга не только непосредственно, а через использование их в промежуточных деталях, например, болт используется в автомобиле, т.к. он используется в двигателе, а двигатель используется в автомобиле.
состоит в описании включения деталей друг в друга не только непосредственно, а через использование их в промежуточных деталях, например, болт используется в автомобиле, т.к. он используется в двигателе, а двигатель используется в автомобиле.
Множество - это неопределяемое понятие, представляющее некоторую совокупность данных. Элементы множества можно отличать друг от друга, а также определять, принадлежит ли данный элемент данному множеству. Над множествами можно выполнять операции объединения, пересечения, разности и дополнения.
Новые множества можно строить при помощи понятия декартового произведения (конечно, есть и другие способы, но они нас в данный момент не интересуют). Декартово произведение нескольких множеств - это множество кортежей , построенный из элементов этих множеств.
Отношение - это подмножество декартового произведения множеств. Отношения состоят из однотипных кортежей. Каждое отношение имеет предикат отношения и каждый n-местный предикат задает n-арное отношение.
Отношение является математическим аналогом понятия "таблица".
Отношения обладают степенью и мощностью . Степень отношения - это количество элементов в каждом кортеже отношения (аналог количества столбцов в таблице). Мощность отношения - это мощность множества кортежей отношения (аналог количества строк в таблице).
В математике чаще всего используют бинарные отношения (отношения степени 2). В теории баз данных основными являются отношения степени 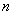 .In mathematics, as a rule, relations are given on infinite sets and have infinite cardinality. In databases, on the contrary, the power relations are finite (the number of stored rows in the tables is always of course).
.In mathematics, as a rule, relations are given on infinite sets and have infinite cardinality. In databases, on the contrary, the power relations are finite (the number of stored rows in the tables is always of course).
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL