Connections and set-theoretic relations on relations

Consider the basic operations on relationships that may be of interest from the point of view of extracting data from relational tables. This union, intersection, difference, extended Cartesian product of relations, as well as special operations on relations: selection, projection and connection.

To illustrate set-theoretic operations on relations, we introduce abstract relations (tables) with some attributes (fields).

R ratio
R.a1	R.a2
A	one
A	2
B	one
B	3
B	four

  CREATE TABLE R
 (a1 CHAR (1), a2 INT, PRIMARY KEY (a1, a2)) 

S ratio
S.b1	S.b2
one	h
2	g
3	h

  CREATE TABLE S
 (b1 INT PRIMARY KEY, b2 CHAR (1)) 

Sampling and projection operations are unary because they work with the same relation.

Fetch operation

The sampling operation is the construction of a horizontal subset, i.e. subsets of tuples with given properties.

The sampling operation works with one relation R and determines the resulting relation that contains only those tuples (strings) of the relation R that satisfy the given condition F (predicate).

or .

Example 5.1 . Sampling operation in SQL.

Sample written as follows:

  SELECT a1, a2
 FROM R
 WHERE a2 = 1 

5.1. Sampling operation in SQL.

Projection operation

The projection operation is the construction of a vertical relation subset, i.e. subsets of tuples obtained by choosing one and excluding other attributes.

The projection operation works with a single R relation and defines a new relation that contains a vertical subset of the R relationship created by extracting the values ​​of the specified attributes and excluding duplicate rows from the result.

Example 5.2 . The projection operation in SQL.

Projection 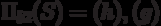written as follows:

  SELECT DISTINCT b2
 FROM S 

5.2. The projection operation in SQL.

The Cartesian product belongs to the main operations on relations.

Cartesian product

The Cartesian product RxS of two relations (two tables) defines a new relation — the result of concatenation (ie, concatenation) of each tuple (each record) from the relation R with each tuple (each record) from the relation S.

  RxS = {(a, 1, 1, h), (a, 2, 1, h), 
      (b, 1, 1, h), ...} 

  SELECT R.a1, R.a2, S.b1, S.b2
 FROM R, S 

5.3. Cartesian product of relations in SQL.

The result of the Cartesian product of the two relations is shown in the table.

Table 5.1.

R x S
R.a1	R.a2	S.b1	S.b2
a	one	one	h
a	one	2	g
a	one	3	h
a	2	one	h
a	2	2	g
a	2	3	h
b	one	one	h
b	one	2	g
b	one	3	h
b	3	one	h
b	3	2	g
b	3	3	h
b	four	one	h
b	four	2	g
b	four	3	h

If one relation has N records and K fields, and the other has M records and L fields, then the relation with their Cartesian product will contain NxM records and K + L fields. The original relationships can contain fields with the same name, then the field names will contain the names of the tables as prefixes to ensure the uniqueness of the field names in the relation obtained as the result of the Cartesian product.

However, in this form (Example 5.3.) The relation contains more information than is usually necessary for the user. As a rule, users are only interested in some part of all combinations of records in a Cartesian product, satisfying some condition. Therefore, instead of the Cartesian product, one of the most important operations of relational algebra is commonly used - the join operation, which is a derivative of the Cartesian product operation. From the point of view of implementation efficiency in relational DBMSs, this operation is one of the most difficult and often is among the main reasons for the performance problems inherent in all relational systems.

Join operation by two relationships (tables)

Joining is a process where two or more tables are combined into one. The ability to combine information from several tables or queries in the form of a single logical set of data determines the wide possibilities of SQL.

In SQL, to specify the type of connection of tables into a logical set of records, from which the necessary information will be selected, the JOIN operation is used in the FROM clause.

Operation format:

  FROM table_name_1 {INNER |  LEFT |  RIGHT} 
     JOIN table_name_2 
 ON join condition 

There are various types of join operations:

• theta connection ;
• equivalence connection ;
• natural compound ;
• external connection , ;
• semi-compound .

Theta join operation

Theta join operation defines a relation that contains tuples from a Cartesian product of relations R and S that satisfy predicate F. Predicate F has the form where instead one of the comparison operators (>,> =, <, <=, =, <>) may be specified.

If the predicate F contains only the equality operator (=), then the connection is called an equivalence connection.

Table 5.2.

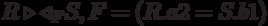R.a1	R.a2	S.b1	S.b2
a	one	one	h
a	2	2	g
b	3	3	h
b	one	one	h

The theta join operation in SQL is called INNER JOIN (inner join) and is used when you need to include all rows from both tables that meet the join condition. The inner join occurs when the values ​​of the fields from different tables are compared in the WHERE clause. In this case, the Cartesian product of the rows of the first and second tables is constructed, and records are selected from the resulting data set that satisfy the join conditions.

In a join environment, fields with the same data type and containing the same kind of data may participate, but they do not have to have the same name.

The data blocks from the two tables are combined as soon as the matching values ​​are found in the specified fields.

If several tables are listed in the FROM clause and the JOIN specification is not used, and the condition in the WHERE clause is used to indicate the correspondence of the fields from the tables, some relational DBMSs (for example, Access) optimize query execution, interpreting it as a join.

If you list a series of tables or queries and do not specify join conditions, the Cartesian (direct) product of all the tables will be selected as the source table.

  SELECT R.a1, R.a2, S.b1, S.b2
 FROM R, S
 WHERE R.a2 = S.b1

     or

 SELECT R.a1, R.a2, S.b1, S.b2
 FROM R INNER JOIN S ON R.a2 = S.b1 

5.4. Theta connection relations in SQL.

Natural compound

A natural connection is a connection by equivalence of two relations R and S, performed for all common attributes, from the results of which one instance of each common attribute is excluded.

Table 5.3.

R.a1	R.a2 or S.b1	S.b2
a	one	h
a	2	g
b	3	h
b	one	h

  SELECT R.a1, R.a2, S.b2
 FROM R, S
 WHERE R.a2 = S.b1

     or 

 SELECT R.a1, S.b1, S.b2
 FROM R INNER JOIN S ON R.a2 = S.b1 

5.5. The natural connection of relationships in SQL.

Example 5.6 . Display information about the goods sold.

  SELECT *
 FROM Transaction, Commodity
 WHERE Transaction. Product Code = Product Product Code

     Or (equivalently)

 SELECT *
 FROM Item INNER JOIN Transaction 
     ON Commodity Product Code = Transaction. Product Code 

5.6. Selection of information about the goods sold.

You can create nested joins by adding a third table to the result of combining two other tables.

Example 5.7 . Get information about the goods, the date of transactions, the number of goods sold and buyers.

  SELECT Commodity. Name, Deal. Amount, Deal.
     Date, Client. Firm
 FROM Client INNER JOIN 
     (Product INNER JOIN Transaction
 ON Product.Product ID = Transaction.Product ID) 
 ON Client.Code Client = Transaction. Client Code 

5.7. A selection of information about the goods, the date of transactions, the number of goods sold and buyers.

Using common table names to identify columns is inconvenient because of their bulkiness. Each table can be assigned a short designation, an alias.

Example 5.8 . Get information about the goods, the date of transactions, the number of goods sold and buyers. The query uses table aliases.

  SELECT T.Name, S.Number, 
        S.Data, K.Firma
 FROM Client AS TO INNER JOIN 
     (Product AS T INNER JOIN
     AS C transaction 
 ON T.KodTovara = S.KodTovara) 
 ON K. Client Code = S. Client Code; 

5.8. A selection of information about the goods, the date of transactions, the number of goods sold and customers using a nickname.

An outer join is similar to an inner join, but the resultant dataset also includes the entries in the join master table, which merge with the empty set of entries in another table.

Which of the tables will be leading determines the type of connection. LEFT - left outer join, leading is a table located to the left of the join type; RIGHT - the right outer join, the leading table is located to the right of the join type.

Left outer join

A left outer join is a join in which the tuples of the relation R that do not have the same values ​​in the common columns of the relation S are also included in the resulting relation.

Table 5.4.

R.a1	R.a2	S.b1	S.b2
a	one	one	h
a	2	2	g
b	one	one	h
b	3	3	h
b	four	null	null

  SELECT R.a1, R.a2, S.b1, S.b2
 FROM R LEFT JOIN S ON R.a2 = S.b1 

5.9. Left external join of relations in SQL.

There is also a right external connection. , so called because the resulting relation contains all the tuples of the right relation. In addition, there is a complete external connection, all the tuples from both relations are placed in its resulting relation, and the null determinants are used to denote mismatched tuple values.

  SELECT R.a1, R.a2, S.b1, S.b2
 FROM R RIGHT JOIN S ON R.a2 = S.b1 

5.10. Right external join of relations in SQL.

Example 5.11 . Display information about all products. For the goods sold, the transaction date and quantity will be indicated. For unsold these fields will remain empty.

  SELECT Item. *, Deal. *
 FROM Item LEFT JOIN Transaction 
 ON Product.Product ID = Transaction.Product ID; 

5.11. Selection of information on all products.

Semi compound

The semi-join operation defines a relation containing those tuples of the relation R that are part of the combination of the relations R and S.

Table 5.5.

R.a1	R.a2
a	one
a	2
b	3
b	one

  SELECT R.a1, R.a2
 FROM R, S
 WHERE R.a2 = S.b1

     or

 SELECT R.a1, R.a2
 FROM R INNER JOIN S ON R.a2 = S.b1 

5.12. Semi-join relationship in SQL.

Join operation

Union (UNION) relations R and S can be obtained as a result of their concatenation with the formation of one relationship with the exception of duplicate tuples. In this case, the relations R and S must be compatible, i.e. have the same number of fields with matching data types. In other words, the relationship must be compatible with the union.

The union of two tables R and S is a table containing all the rows that are in the first table R, in the second table S, or in both tables at once.

  SELECT R.a1, R.a2 
 FROM R
 UNION
 SELECT S.b2, S.b1 
 FROM S 

5.13. Combining relations in SQL.

Intersection operation

INTERSECT operation defines a relation that contains tuples that are present both in relation to R and in relation to S. Relations of R and S must be compatible with the union.

The intersection of two tables R and S is a table containing all rows that are present in both source tables at the same time.

  SELECT R.a1, R.a2
 FROM R, S
 WHERE R.a1 = S.b1 AND R.a2 = S.b2

    or

 SELECT R.a1, R.a2
 FROM R
 WHERE R.a1 IN    
     (SELECT S.b1 FROM S
      WHERE S.b1 = R.a1) AND R.a2 IN
          (SELECT S.b2
           FROM S
           WHERE S.b2 = R.a2) 

5.14. The intersection of relations in SQL.

Difference operation

The difference (EXCEPT) RS of the two relations R and S consists of tuples that exist in relation to R, but are absent in relation to S. Moreover, the relationship R and S must be compatible with the union.

The difference between the two tables, R and S, is a table that contains all the rows that are present in table R, but not in table S.

  SELECT R.a1, R.a2
 FROM R
 WHERE NOT EXISTS 
     (SELECT S.b1, S.b2
      FROM S
      WHERE S.b1 = R.a2 AND S.b2 = R.a1) 

5.15. Difference relations in SQL.

Relational division operation

The result of the division operation R: S is the set of tuples of the relation R defined on the set of attributes C, which correspond to the combination of all the tuples of the relation S.

  T1 = P 

C

  (R);
 T2 = P 

C

  ((SX T1) -R);
 T = T1 - T2. 

The relation R is defined on the set of attributes A, and the relation S on the set of attributes B, and and C = A - B.

Let A = {name, gender, height, age, weight}; B = {name, gender, age}; C = {height, weight}.

Table 5.6.

R ratio
name	floor	growth	age	weight
a	well	160	20	60
b	m	180	thirty	70
c	well	150	sixteen	40

S ratio
name	floor	age
a	well	20

T1 = P C (R)
growth	weight
160	60
180	70
150	40

TT = (SX T1) -R
name	floor	age	growth	weight
a	well	20	180	70
a	well	20	150	40

T2 = P C ((SX T1) -R)
growth	weight
180	70
150	40

T = T1-T2
growth	weight
160	60

Example 5.16 . Division of relations in SQL.

• Creating relationship R

    CREATE TABLE R
   (i int primary key,
   name varchar (3),
   gender varchar (3),
   int growth,
   age int,
   weight int) 

  5.16a. Division of relations in SQL.
• Creating relationship S

    CREATE TABLE S
   (i int primary key,
   name varchar (3),
   gender varchar (3),
   age int) 

  5.16b. Division of relations in SQL.
• Creating a T1 relationship

    CREATE VIEW T1
   AS 
   SELECT height weight
   FROM R 

  5.16c. Division of relations in SQL.
• Creating a TT relationship

    CREATE VIEW TT AS
   SELECT S. name, S. floor, S. age, 
          T1.rost, T1.ves
   FROM S, T1 

  5.16d. Division of relations in SQL.
• Creating a T2 relationship

    CREATE VIEW T2
   AS
   SELECT TT. Growth, TT. Weight
   FROM TT
   WHERE NOT EXISTS 
       (SELECT R. growth, R. weight
        FROM R
        WHERE TT. Name = R. Name AND TT. Paul = R. Paul
              AND TT. Age = R. Age 
              AND TT.rost = R.rost 
  		    AND TT. Weight = R. weight) 

  5.16e. Division of relations in SQL.
• Creating relationship T

    SELECT T1. growth, T1. weight
   FROM T1
   WHERE NOT EXISTS 
       (SELECT T2.rost, T2.ves
        FROM T2
        WHERE T1.ros = T2.rost AND T1.ves = T2.ves) 

  5.16f. Division of relations in SQL.

See also

• 5.1. Relational algebra
• Connections and set-theoretic relations on relations
• 4. Relational algebra