Lecture
The previous section was devoted to the issues of presenting in the database one of the most important types of information about the subject area - data integrity constraints . In particular, the following important types of integrity constraints were considered, such as constraints of potential keys and restrictions of descriptor integrity. These one of the most important types of integrity constraints are, however, special cases of the representation in the database of various kinds of dependencies between entities of the information system domain. Indeed, the potential key constraint is that the values of one attribute (s) uniquely determine the values of other attributes in a relation. The constraint of external keys indicates the dependence of the attribute values of one relation on the attribute values of another relation. Undoubtedly, one of the most important components of a database design task is to present as diversely as possible the various dependencies between the entities of the subject area and provide a mechanism for maintaining the data stored in the system during its operation in the state corresponding to these relationships. However, the material presented in the previous sections does not allow to answer the question: how best to present this subject area in the form of a specific set of basic (stored) relational relations.
This section discusses how to build a “good” relational database. As mentioned above, the relational database is a set of normalized table-relations. On the basis of the material already studied, it should be clear that the same information on the subject area, generally speaking, can be represented using different sets of relationships, to the point that all information can be represented using one normalized supertables. It is obvious that such various forms of the logical structure of the database will not be fully equivalent in terms of convenience and efficiency of using the information contained in them, the ability to maintain data in a coherent state.
The task of designing a database is to choose the most optimal structure of basic relations.
The materials of this section are just dedicated to clarifying the criteria that allow choosing the “best” variants of the logical structure of the database, as well as defining methods that allow consciously using formal, equivalent from the point of view of the information content of the database transformations to optimize the logical structure of its relations.
When solving these issues, one of the fundamental concepts of the theory of relational databases is the concept of functional dependence.
Functional Dependency is a many-to-one relationship between sets of attribute values within a relationship. The relationship is understood in the sense of a variable relationship, which implies that this kind of dependence between attribute values takes place in any specific state of the relationship.
Informally speaking, the functional dependence between attribute values is that the value of one attribute (possibly a composite one) uniquely determines the value of another attribute. This kind of relationship between the attributes of a relationship is already familiar to us. For example, the values of attributes that are the key of a relationship always uniquely determine the values of all other attribute relations.
A more rigorous formulation of the definition of functional dependence is as follows.
Let R be a relation variable, and X and Y be arbitrary subsets of the attribute set of the relation R. It is said that the value of Y functionally depends on the value of X if and only if for any valid value of the relation R each value of X is associated exactly with one value of Y .
Symbolically, a functional relationship is designated X → Y. This entry reads as follows: X functionally defines Y or Y functionally depends on X.
At the same time, the attributes of X are called the determinant , and the attributes of Y are the dependent part of the functional dependency.
An important clarification in this definition, indicating that a functional relationship exists for all possible relationship states, indicates that the definition of functional dependencies for a relationship relates to a type of indication of the constraints of the integrity of the relationship .
In the concrete relation usually not one, but a set of functional dependences is present. For example, in the relation shown in fig. 10.1, the key of which is the composite attribute {CODE_STUDIO, DISCIPLINE}, there are several functional dependencies.
|
{CODE_STUDIO, DISCIPLINE} → {NAME_STUD}
{CODE_STUDIO, DISCIPLINE} → {EVALUATION}
{CODE_STUDIO, DISCIPLINE} → {NAME_STUD, ESTIMATION}
{CODE_STUDIO, DISCIPLINE, NAME_STUD} → {EVALUATION}
{CODE_STUDIO, DISCIPLINE} → {CODE_STUD}
{CODE_STUDIO, DISCIPLINE, NAME_STUD} → {DISCIPLINE}
However, not all functional dependencies taking place in relation to them are of practical interest, in particular, the so-called trivial functional dependencies.
A functional dependency is called trivial if and only if the right (dependent) part of the symbolic notation of this dependency is a subset of its left part (determinant).
Thus, in the example above, the dependencies
{CODE STUD, DISCIPLINE} → {CODE STUD} and
{CODE_STUDIO, DISCIPLINE, NAME_STUD} → {DISCIPLINE}
are trivial. It is clear that the fixation of the presence between attributes of such dependencies does not carry any additional semantic load.
Speaking of functional dependencies, it can also be noted that some dependencies can be derived from other functional dependencies. Addiction
{CODE_STUDIO, DISCIPLINE} → {NAME_STUD, ESTIMATION}
follows from dependencies
{CODE_STUDIO, DISCIPLINE} → {NAME_STUD} and
{CODE_STUDIO, DISCIPLINE} → {EVALUATION}.
It is obvious that adding to the set of functional dependencies derived from them also does not add any new information about the nature of dependencies between the attributes. Nevertheless, the fact that some dependencies can be deduced from others suggests that there can exist sets of dependencies equivalent to each other in terms of the information about the subject area reflected by them.
The set of all functional dependencies that are defined by a given set of functional dependencies S, that is, they can be derived from these dependencies, is called a closure of the set of dependencies S and is denoted by S + .
The rules that allow us to derive its closure S + from this set of dependencies S , called Armstrong's rules, have the following form.
Let A , B , C and D be arbitrary subsets of the set of attributes of a given relation R , then such rules apply to them.
These three rules are a complete set that allows you to display all the dependencies that make up the S + closure of the S dependency sets. From these rules, to simplify the task of practical computation of the closure of S + , several consequences can be derived.
In practice, it is usually more important not to find the set of dependencies S + , which are the closure of the set of functional dependencies S , but to find the answer to the question whether this particular functional dependence X → Y can be inferred from the existing set of dependencies S.
We give some more useful definitions.
Let S1 and S2 be two sets of functional dependencies. If any functional dependency that is a dependency of the set S1 is also a dependency of the set S2, that is, if S1 + is a subset of S2 + , then S2 is called a cover for S1.
If S2 is a coating for S1, and S1 is a coating for S2, that is, if S1 + = S2 + , then S1 and S2 are equivalent .
A functional dependence is called left irreducible (or functionally complete ) if no attribute can be dropped from its determinant without changing the closure of S + (without transforming the set S into some set that is not equivalent to it).
Or, less strictly, but more simply:
A functional dependency is called left irreducible (or functionally complete ) if no attribute can be omitted from its determinant without breaking this dependency.
Normal forms
As mentioned above, the relational model supports only normalized relations, that is, relations that contain only scalar (atomic) attribute values. This form of relationship in the theory of normalization is called the first normal form (abbreviated 1NF). This, however, is not the only normal form of relational representation. Currently, besides the first normal form, five others are known. Why is it necessary to introduce new normal forms and transform relations into normal forms of a higher order? The fact is that relationships that are in the first normal form may have a number of undesirable properties. Consider as an example, the ratio of CERTAINABILITY, presented in Figure 10.2.
|
Fig. 10.2. An example of a relationship in first normal form.
It is easy to see that in this respect there is a certain redundancy. Indeed, in many tuples information is duplicated on which student’s code corresponds to a particular student’s last name. The presence of redundancy of information is considered as a lack of attitude. And the point here is not only and not so much that duplication of information leads to an increase in the amount of memory required to store information in a computer system. Much more important is that redundancy makes it difficult to maintain information contained in a holistic state. For example, in the case of a change in the student's last name, the corresponding attribute values in all tuples related to this student should be corrected in the relation; otherwise, the relation data will be in a contradictory state.
Normalization of relations of a relational database is a formalized transformation of these relations in order to eliminate possible undesirable properties in them, which in general can have a logical structure of relations that are in the first normal form without loss of information of the original relationship, including dependencies that have place between its attributes.
The theory of normalization allows, for example, to answer the question - which of the two logical structures of relations is preferable: relation
R1 {CODE_STUDE, NAME_STUD, FACULTY, DISCIPLINE, EVALUATION}
or structure of two relationships
R2 {CODE_STUD, NAME_STUD, FACULTY} and R3 {CODE_STUD, DISCIPLINE, EVALUATION}.
Normal forms of higher order are the first, second and third normal forms defined by Codd (Codd) (1NF, 2NF and 3NF), the so-called Boyes – Codd normal form (NFBC) and the fourth one defined by Fagin and the fifth normal form (4NF and 5NF).
Fig. 10.3 shows that the sets of relations that are in various normal forms turn out to be nested in each other. So, for example, the relation in 3NF will be simultaneously in both 2NF and 1NF, but not necessarily in the NFBK. The relation that is in 5NF will simultaneously be in all other normal forms.
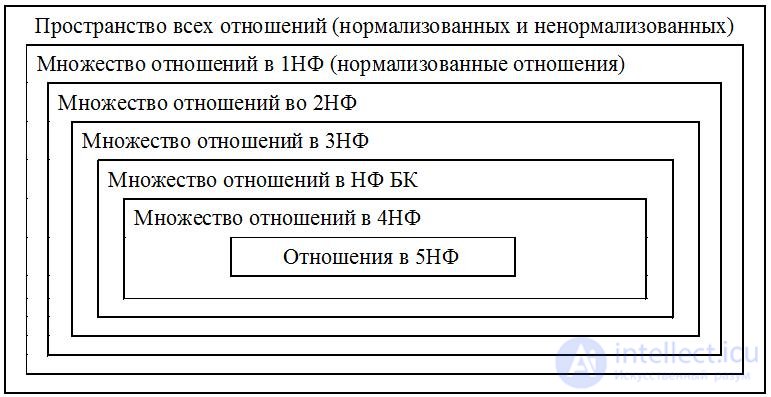
Below it will be shown that the transformation of relations into a normal form of a higher degree is in a certain sense “more desirable”. It is important to immediately note that the normalization of relations should be necessarily reversible . This means that the transformation of relations into normal forms of a higher degree is carried out without losing the information that these relations represent , since the possibility of the inverse transformation is always guaranteed, that is, the complete restoration of the original information.
The procedure of normalization of relations consists in their division, that is, decomposition, into other relations that are in normal forms of a higher level. Moreover, as mentioned above, such a decomposition should be carried out without loss of information contained in the original relation. Thus, in the implementation of the process of normalization of relations, it is not of any transformation that is of interest, but only those that do not lead to the loss of useful information.
Consider an example. Let the initial relation have the form presented in Figure 10.4.
|
Figure 10.5 shows that this relationship can be broken into two relationships in three different ways.
Ratio 1a
|
Attitude 2a
|
||||||||
Attitude 1b
|
Attitude 2b
|
||||||||
Attitude 1c
|
Attitude 2c
|
If you look closely at the three options for decomposition of relations, you can see that in the first case (option a), when the relations are split, the original information is not lost. Indeed, the original relationship Relationship 1 can be restored in its previous form by the operation of the natural connection of relations Relationship 1a and Relationship 2a by the attribute STUDENT_CODE.
In the second and third cases, part of the information contained in relation to Attitude 1 is lost, namely: they lose information which of the namesake students Ivanov learns from the physical and what at the history departments. It is easy to see that the natural connection of the Relationship 1b and the Relationship 2b in their only common attribute PERSON_NAME, which is shown in Fig.10.6, does not allow to get the initial state of the relationship Ratio 1.
|
The important question of whether or not a loss of information occurs during the decomposition of relations is closely related to the concept of functional dependence . You can pay attention to the fact that in the previous example, when carrying out the decomposition represented by option “b”, the functional dependence of the FACTORY attribute on the attribute STANDING CODE was lost, and in the decomposition of option “c”, the attribute POST_NAME from the attribute STUDENT CODE was lost.
The answer to the question in which case the decomposition of a relation is reversible is given by the Heath theorem.
Hez's theorem. Let R {A, B, C} be a relation, and A, B, and C be attributes of this relation. If in relation to R there is a functional dependence A → B, then the ratio R is equal to the connection of its projections R 1 {A, B} and R 2 {A, C}.
In other words, the functional dependency must be preserved and the determinant of this dependency (attribute A ) must be present in both the resulting relationships. In the example given in Fig. 10.4, two functional dependencies take place: CODE → STUDENT_NAME and STUDENT_CODE → FACULTY, and therefore, according to the Hez theorem, Ratio 1 can be broken down into two relations that are its projections, namely, Ratio 1a {STUDENT_CODE, NAME_TITLE. {STANDARD CODE, FACULTY}, without loss of information. In any other way of decomposition, one of these functional dependencies is lost.
A relation is in the first normal form (1NF) if and only if the domains of all its attributes contain only scalar values.
As mentioned above, a relation that is in the first normal form may have undesirable properties.
Let us imagine that we need to store in the database information about the student’s personal code (identifier), his last name, and his grades obtained in specific disciplines. For these purposes, you can enter the following attributes: STANDING CODE, STUDENT_NAME, DISCIPLINE and EVALUATION. Between these attributes, functional dependencies take place, represented by arrows in Figure 10.7.
Fig. 10.7. Functional Dependency Diagram
Эти зависимости показывают, что пара значений атрибутов {КОД_СТУДЕНТА, ДИСЦИПЛИНА} однозначно определяет значение атрибута ОЦЕНКА (конкретный студент может иметь по конкретной дисциплине только одну оценку), а значение атрибута КОД_СТУДЕНТА однозначно определяет значения атрибутаИМЯ_СТУДЕНТА (студент имеет одну фамилию).
Можно отметить также, что в отношении присутствует еще и приводимая функциональная зависимостьатрибута от ключа отношения, а именно, зависимость {КОД_СТУДЕНТА, ДИСЦИПЛИНА}→{ИМЯ_СТУДЕНТА}, обозначенная на рис.10.7 пунктиром.
Какова должна быть структура отношений для хранения данных, соответствующих этому примеру? Рассмотрим простейший случай, когда все приведенные атрибуты включены в схему одного отношения, назовем его Экзамен, как это показано на рис.10.8.
|
Это отношение находится в первой нормальной форме, так как все значения его атрибутов являются скалярными. Единственным потенциальным ключом этого отношения является составной атрибут {КОД_СТУДЕНТА, ДИСЦИПЛИНА}, так как эта пара атрибутов однозначно определяет значения кортежейотношения, в то время как каждый из атрибутов КОД_СТУДЕНТА и ДИСЦИПЛИНА по отдельности таким свойством не обладает.
Хорошо видно, однако, что содержащиеся в этом отношении данные избыточны. Так, в частности, в этом отношении для каждого студента многократно дублируется информация о его фамилии.
Избыточность в отношении приводит к возникновению нежелательных факторов, или к аномалиям , при осуществлении с этим отношением операций, связанных с изменением данных, а именно операций INSERT (вставка кортежа), DELETE (удаление кортежа) и UPDATE (обновление значений атрибута какого-либо кортежа). Рассмотрим, в чем состоят эти аномалии.
Операция INSERT . В отношение ЭКЗАМЕН нельзя вставить кортеж с данными о коде студента и его фамилии (например, запись о том, что студент с кодом С4 имеет фамилию Лукин), если мы не имеем данных о том, что этот студент сдавал хотя бы одну дисциплину. Действительно, в этом случае не может быть задано значениепервичного ключа для кортежа, соответствующего этой записи, так как неизвестно значение атрибутаДисциплина.
Операция DELETE . При удалении информации о том, что конкретный студент сдавал какую-либо дисциплину, например, если мы хотим аннулировать ошибочно введенную запись о сдаче студентом с кодом С9 экзамена по иностранному языку, мы можем потерять информацию о фамилии этого студента из-за того, что удаляемый кортеж был единственным кортежем, содержащем информацию о нем.
UPDATE operation . The value of the attribute student_name is repeated in this respect many times for each specific value of the attribute STUDENT CODE. Therefore, in the case when, for example, for a student with CAS2, it is necessary to change the surname (married), these changes will need to be made for all tuples related to this student. In addition to the cumbersome performance of the same operation of adjusting the attribute value for a large number of records in this case, a more unpleasant situation is possible. If for one reason or another (for example, due to a system failure), for any tuples of the relationship, such a correction will not be produced, relations will be tuples with conflicting data (in some tuples C2 will correspond to one surname, and in others for the same code will be indicated another surname.
The indicated anomalies, however, can be eliminated if the initial relation is replaced by two projections of it - the STUDENTS and PERFORMANCE relationships shown in Figure 10.9.
|
|
Diagrams of functional dependencies for these two relationships are presented in Figure 10.10.
Fig. 10.10. Diagrams of the functional dependencies of the STUDENTS relationship and RESEARCH
Можно видеть, что рассмотренные выше проблемы, имеющие место в отношении ЭКЗАМЕН, связанные с обновлением данных, в данном случае оказываются преодоленными.
Операция INSERT . Информация о том, что студент с кодом С4 имеет фамилию Лукин, может быть сохранена путем вставки соответствующего кортежа в отношение СТУДЕНТЫ независимо от того, имеются или нет данные о сдаче этим студентом какой-либо учебной дисциплины.
Операция DELETE . Информация о том, что студент с кодом С9 сдавал экзамен по иностранному языку может быть удалена из отношения УСПЕВАЕМОСТЬ без потери информации о фамилии этого студента.
Операция UPDATE . Для изменения фамилии у студентки с кодом С2 необходимо скорректировать значение соответствующего атрибута в единственной записи отношения СТУДЕНТЫ.
Сравнивая диаграммы функциональных зависимостей на рис.10.7 и 10.10, можно увидеть, что произведенная декомпозиция отношения Экзамен на два отношения СТУДЕНТЫ и Успеваемость привела к исключению из отношений приводимой функциональной зависимости атрибута от ключа отношения, а именно зависимости {Код_студента, Дисциплина}→{ИМЯ_студента}, обозначенной на рис.10.7 пунктиром.
Указанная зависимость является избыточной, так как, на самом деле, она является следствием наличия неприводимой функциональной зависимости {Код_студента}→{ИМЯ_студента}, что хорошо видно из диаграммы на рис.10.7.
Теперь можно дать определение второй нормальной формы отношения.
Отношение находится во второй нормальной форме (2НФ) тогда и только тогда, когда оно находиться впервой нормальной форме и каждый неключевой атрибут неприводимо (функционально полно) зависит от первичного ключа.
Напомним, что неключевым мы называем атрибут, который не входит в состав ключа отношения.
Оба отношения – СТУДЕНТЫ и Успеваемость, полученные в результате декомпозиции отношения Экзамен, находятся во второй нормальной форме, так как их неключевые атрибуты ИМЯ_студента, Факультет иОценка зависят от первичных ключей этих отношений, соответственно, {Код_студента} и {Код_студента,Дисциплина} неприводимо .
Обратившись к приведенной ранее теореме Хеза, можно видеть, что для любого отношения, находящегося впервой нормальной форме, всегда возможно без потерь информации путем его декомпозиции преобразовать к двум отношениям, находящимся во второй нормальной форме.
Еще раз обращаем внимание на то, что декомпозиция эта осуществляется без потерь информации. Исходное отношение ЭКЗАМЕН (рис.10.8) всегда может быть восстановлено путем соединения двух выходных отношений студенты и УСПЕВАЕМОСТЬ (рис.10.9) по их общему атрибуту КОД_СТУДЕНТА.
Consider the following example. Представим себе, что требуется хранить в базе данных информацию о том, в каком общежитии живет студент с указанием адреса общежития. Для этих целей можно ввести следующие атрибуты: КОД_СТУДЕНТА, ОБЩЕЖИТИЕ и АДРЕС. Между указанными атрибутами имеют местофункциональные зависимости, представленные на рис.10.11.
Fig. 10.11. Диаграмма функциональных зависимостей между атрибутами СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС
Эти функциональные зависимости означают тот факт, что студент может жить только в одном общежитии и у общежития может быть только один адрес.
Для хранения рассматриваемой информации может быть использовано отношение СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС, приведенное на рис.10.12.
|
Это отношение находятся во второй нормальной форме. Действительно, как это видно из диаграммы на рис.10.11, между его неключевыми атрибутами общежитие и адрес и ключом отношения, которым является атрибут КОД_СТУДЕНТА, имеет место неприводимая функциональная зависимость . Поэтому в данном отношении не может быть аномалий, связанных с наличием приводимой функциональной зависимости у отношений, не находящихся во второй нормальной форме. Тем не менее, при внимательном рассмотрении этого отношения можно увидеть, что структура отношения на рис.10.12 не лишена недостатков.
Indeed, the same values of the address of the hostel are repeated many times for each student living in this hostel. This redundancy also leads to the occurrence of anomalies when performing an update operation on the relation.
INSERT operation . We cannot include in the database information about the address of a new dormitory as long as we do not have data on at least one student living in this dormitory.
DELETE operation . When deleting information about students living in a dormitory, you can lose information about the address of the hostel. For example, if you delete a tuple for a student with code C9, we lose the address information of the hostel №2.
Операция UPDATE . Дублирование информации об адресах общежитий приводит к тому, что в случае переименования названия улицы, на которой расположено общежитие, необходимо внести изменения в адрес общежития для всех проживающих в нем студентов. При некорректном завершении такой операции в отношении могут оказаться кортежи с противоречивой информацией – для одного общежития два значения адреса, что противоречит имеющей место функциональной зависимости атрибута адрес от атрибутаобщежитие (см. рис. 10.11).
Очевидно, что причиной этих аномалий уже не является наличие приводимой функциональной зависимостинеключевых атрибутов от ключа, как это было в примере, рассмотренном в предыдущем разделе. Таких зависимостей в этом отношении нет. Оно находится во второй нормальной форме и его неключевые атрибуты общежитие и адрес зависят от ключа (атрибут КОД_СТУДЕНТА неприводимо.
На этот раз причиной имеющих место аномалий обновления является наличие транзитивнойфункциональной зависимости атрибута адрес от атрибута Код_студента, показанной на рис.10.13 пунктирной стрелкой.
Решение обозначенной проблемы также состоит в декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕСна два отношения для исключения транзитивной функциональной зависимости. Результатом такой декомпозиции являются два отношения, представленные вместе с диаграммами их функциональных зависимостей на рис.10.14.
|
|
Данная декомпозиция является декомпозицией без потерь. Исходное отношение может быть восстановлено путем операции соединения отношений СТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС по атрибутуобщежитие. Также при декомпозиции не теряется информация о функциональной (транзитивной) зависимости КОД_СТУДЕНТА→АДРЕС, так как она может быть выведена из зависимостейКОД_СТУДЕНТА→ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ→АДРЕС.
Не трудно видеть, что данная декомпозиция решает проблемы с приведенными примерами аномалий операций обновления. Действительно, информация об адресе нового общежития может быть легко вставлена в отношение ОБЩЕЖИТИЕ_АДРЕС, операция удаления информации о студенте из отношенияСТУДЕНТ_ОБЩЕЖИТИЕ не затрагивает информации об адресах общежитий, и, наконец, изменение названия улицы для общежития производится модификацией значения атрибута АДРЕС в соответствующем (единственном) кортеже отношения ОБЩЕЖИТИЕ_АДРЕС.
Декомпозиция отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС переводит его в два отношенияСТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС, находящиеся уже в третьей нормальной форме . Определение этой нормальной формы имеет следующий вид.
Отношение находится в третьей нормальной форме (3НФ) тогда и только тогда, когда оно находится вовторой нормальной форме и каждый его неключевой атрибут нетранзитивно зависит от потенциального ключа.
Приведенные выше отношения студент и УСПЕВАЕМОСТЬ на рис.10.9, СТУДЕНТ_ОБЩЕЖИТИЕ иОБЩЕЖИТИЕ_АДРЕС на рис.10.14 удовлетворяют этому определению, поэтому все они находятся в третьей нормальной форме.
Говоря о декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС на рис.10.12 с целью преобразования его в два отношения, находящиеся в третьей нормальной форме, следует обратить внимание на то, что кроме приведенного на рис.10.14, возможен другой вариант разбиения его на два отношения. Этот вариант представлен на рис.10.15.
|
|
Рис.10.15. Другой вариант декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС
Можно видеть, что соединение этих двух отношений по атрибуту КОД_СТУДЕНТА обеспечивает восстановление данных исходного отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС. Существенным, однако, является то, что при такой декомпозиции в этих отношениях оказалась утраченной функциональная зависимость атрибута АДРЕС от атрибута ОБЩЕЖИТИЕ, то есть зависимость ОБЩЕЖИТИЕ→АДРЕС, имеющая место в исходном преобразуемом отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС.
В предыдущем варианте декомпозиция устраняла транзитивную функциональную зависимость, при этом информация не терялась, так как эта зависимость может быть выведена из оставшихся по правиламАрмстронга (см. раздел 10.1). В рассматриваемом же варианте вместо транзитивной зависимости была потеряна зависимость ОБЩЕЖИТИЕ→АДРЕС, которая не выводится из остальных. Необходимость поддержания в базе данных такой зависимости делает в этом случае возможные изменения значений атрибутов ОБЩЕЖИТИЕ и АДРЕС, теперь находящихся в разных отношениях, зависимыми друг от друга.
Действительно, при изменении значения атрибута общежитие в каком-либо кортеже отношениястудент_общежитие мы должны произвести соответствующие изменения атрибута АДРЕС в отношенииСТУДЕНТ_АДРЕС. Следовательно, необходимость поддержания функциональной зависимостиОБЩЕЖИТИЕ→АДРЕС из зависимости между атрибутами одного отношения превратилась в ограничение целостности, накладываемое на два отношения и реализуемое гораздо более сложно.
При первом же варианте декомпозиции, представленном на рис.10.14, функциональная зависимостьОБЩЕЖИТИЕ→АДРЕС, порождающая в отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС нежелательнуютранзитивную зависимость СТУДЕНТ→АДРЕС преобразуется в отношении ОБЩЕЖИТИЕ_АДРЕС в функциональную зависимость атрибута от первичного ключа. Ограничение целостности, задаваемое такой зависимостью, в этом случае привести в действие гораздо проще. Оно автоматически обеспечивается путем наложение ограничений на уникальность первичного ключа.
Таким образом, при преобразовании отношения из второй в третью нормальную форму необходимо выбирать вариант декомпозиции с независимыми проекциями.
Риссанен (Rissanen) показал следующее.
Проекции R1 и R2 отношения R независимы в рассмотренном выше смысле тогда и только тогда, когда:
Второй вариант декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС, представленный на рис.10.15, не удовлетворяет правилу Риссанена, поэтому функциональная зависимость ОБЩЕЖИТИЕ→АДРЕС, имеющая место в отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС, не может быть выведена из функциональных зависимостей, имеющихся в отношениях СТУДЕНТ_ОБЩЕЖИТИЕ и СТУДЕНТ_ АДРЕС.
Once again we draw attention to the fact that the presence of certain functional dependencies between the attributes of relations is a reflection of the semantics of the subject area, its semantic content and cannot be determined based on the specific values of the attributes of relations at some point in time. In other words, the description and maintenance of functional dependencies is one of the formulations of the integrity of the database that must be performed in any state of the database relationship.
In the previous two sections, the transformation of relations into the second and third normal form was considered on the example of relations having a single potential (or primary) key. For this kind of relationship, the conversion to the third normal form solves all the undesirable effects listed above associated with the restriction of functional dependencies. In practice, however, more complicated cases are possible:
It turns out that in these more complex cases, the transformation of relations into a third normal form does not always provide a solution to undesirable problems associated with anomalies of update operations. To eliminate them, another normal form was introduced, called the Beuys normal form - Codd or abbreviated NFBC. (Although Date [1] points out that the definition of this normal form was
продолжение следует...
Часть 1 Database Design
Часть 2 10.7 Multiple dependencies and fourth normal form - Database Design
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL