Lecture
The basics of the relational data model were first outlined in an article by E. Codd [43] in 1970. This work served as a stimulus for a large number of articles and books in which the relational model was further developed. The most common interpretation of the relational data model belongs to K. Data [11]. According to Data, the relational model consists of three parts:
The structural part describes which objects are considered by the relational model. It is postulated that the only data structure used in the relational model is normalized n-ary relations.
The integral part describes a special type of constraints that must be satisfied for any relationship in any relational database. This is entity integrity and foreign key integrity .
The manipulation part describes two equivalent ways to manipulate relational data — relational algebra and relational calculus .
This chapter discusses the structural part of the relational model.
Any data used in programming has its own data types.
Important! The relational model requires that the types of data used are simple .
To clarify this statement, consider what data types are generally considered in programming. As a rule, data types are divided into three groups:
Simple, or atomic, data types do not have an internal structure. Data of this type is called scalar . Simple data types include the following types:
Various programming languages can expand and refine this list by adding such types as:
Of course, the concept of atomicity is rather relative. So, the string data type can be considered as a one-dimensional array of characters, and the whole data type as a set of bits. The only important thing is that when moving to such a low level, the semantics (meaning) of the data are lost. If a string expressing, for example, the surname of an employee, is decomposed into an array of characters, then the meaning of such a string as a whole is lost.
Structured data types are designed to define complex data structures. Structured data types are constructed from constituent elements, called components, which, in turn, may have a structure. The structured data types include the following data types:
From a mathematical point of view, an array is a function with a finite domain of definition. For example, consider a finite set of natural numbers
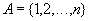
called a set of indices. Display
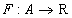
from the set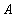 
into a set of real numbers 
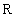sets a one-dimensional real array. The value of this function for some index value 
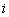called an array element corresponding to 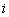. Similarly, you can set multidimensional arrays.
A record (or structure) is a tuple of a Cartesian product of sets. Indeed, a record is a named ordered set of elements.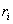 
each of which belongs to a type 
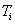. Thus recording 
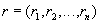there is an element of the set 
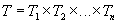. By declaring new record types based on existing types, the user can construct arbitrarily complex data types.
Common to structured data types is that they have an internal structure that is used at the same level of abstraction as the data types themselves.
We explain this as follows. When working with arrays or records, you can manipulate an array or record both with a single whole (create, delete, copy whole arrays or records), and elementwise. For structured data types, there are special functions - type constructors that allow you to create arrays or records from elements of simpler types.
Working with simple data types, for example with numeric ones, we manipulate them as indivisible whole objects. To "see" that the numeric data type is actually complex (is a set of bits), you need to go to a lower level of abstraction. At the level of program code, it will look like assembly inserts into code in a high level language or the use of special bitwise operations.
The reference data type ( pointers ) is intended to provide the ability to point to other data. Pointers are typical for procedural type languages that have the concept of a memory area for storing data. Reference data type is designed to handle complex changing structures, such as trees, graphs, recursive structures.
Actually, for the relational data model, the type of data used is not important. The requirement that the data type is simple should be understood so that relational operations should not take into account the internal data structure . Of course, the actions that can be performed with the data as a whole should be described, for example, data of a numeric type can be added, a string can be concatenated, etc.
From this point of view, if we consider the array, for example, as a whole and not use elementwise operations, then the array can be considered a simple data type. Moreover, you can create your own, arbitrarily complex data type, describe possible actions with this data type, and if operations do not require knowledge of the internal data structure, then this data type will also be simple from the point of view of relational theory. For example, you can create a new type - complex numbers as a record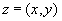 
where 
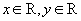. You can describe the functions of addition, multiplication, subtraction and division, and all actions with components 
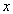and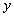 
perform only inside these operations. Then, if in operations with this type to use only the described operations, then the internal structure does not matter, and the data type from the outside looks like atomic.
That is how some post-relational database management systems work with arbitrarily complex data types created by users.
In a relational data model, the concept of a data type is closely related to the concept of a domain, which can be considered a refinement of a data type.
Domain is a semantic concept. A domain can be considered as a subset of the values of a certain data type with a specific meaning. A domain is characterized by the following properties:
For example, domain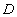 
meaningful “employee age” can be described as the following subset of the set of natural numbers:
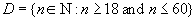
If a data type can be considered a set of all possible values of a given type, then the domain resembles a subset in this set.
The difference of a domain from the notion of a subset is precisely in that the domain reflects the semantics defined by the subject area. There may be several domains that match as subsets, but carry a different meaning. For example, the domains “Weight of a Part” and “Available Quantity” can be equally described as a set of non-negative integers, but the meaning of these domains will be different, and these will be different domains.
The primary meaning of domains is that domains limit comparisons . It is incorrect, from a logical point of view, to compare values from different domains, even if they are of the same type. This is the meaningful limitation of domains. The syntactically correct query is to "give a list of all parts for which the weight of the part is greater than the available quantity" does not correspond to the meaning of the concepts "quantity" and "weight".
Remark The concept of a domain helps to correctly model the subject area. When working with a real system, in principle, a situation is possible when you need to respond to the request given above. The system will give the answer, but it will probably be meaningless.
Remark Not all domains have a logical condition that limits the possible values of the domain. In this case, the set of possible domain values coincides with the set of possible values of the data type.
Remark It is not always obvious how to set a logical condition that limits the possible values of the domain. I will be grateful to the one who will lead me to a condition on a string data type that defines the employee's surname domain. It is clear that strings that are last names should not begin with numbers, official symbols, with a soft sign, etc. But is the name “Ggggggyyyyyyy” valid? Why not? Obviously not! Or maybe someone out of spite would call himself that. Difficulties of this kind arise because the meaning of real phenomena is far from always formally described. Simply, we, like all people, intuitively understand what a surname is, but no one can give such a formal definition that would distinguish surnames from strings that are not last names. The way out of this situation is simple - to rely on the mind of the employee who enters the names into the computer.
The fundamental notion of a relational data model is the notion of a relation . In the definition of the concept of relationship we will follow the book of K. Data [11].
Definition 1. A relationship attribute is a pair of .
Attribute names must be unique within the relationship. Often, the attributes of a relationship match the names of the corresponding domains.
Definition 2 . Attitude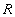 
defined on multiple domains 
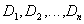(not necessarily different), contains two parts: the heading and the body.
The relationship header contains a fixed number of relationship attributes:
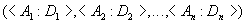
The relation body contains many relation tuples. Each relation tuple is a set of pairs of the form :
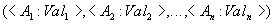
such that value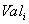 
attribute 
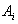belongs to domain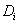 
The relationship is usually written as:
,
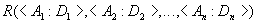or shorter
,
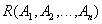or simply
.
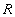The number of attributes in a relationship is called the degree (or -arnost ) of the relationship.
The power of a set of relationship tuples is called the ratio power .
Returning to the mathematical concept of relationship, introduced in the previous chapter, we can draw the following conclusions:
Conclusion 1 . The relationship header describes the Cartesian product of the domains on which the relationship is given. The header is static, it does not change while working with the database. If attributes are changed, added or deleted, then the result is a different relationship (even if with the same name).
Conclusion 2 . The relation body is a collection of tuples, i.e. subset of Cartesian product of domains. Thus, the relation body itself is a relation in the mathematical sense of the word. The relationship body can change while working with the database - tuples can be changed, added and deleted.
Example 1 Consider the relationship "Employees" set on the domains "Number_of the employee", "Last Name", "Salary", "Number_ of the Department". Because Since all domains are different, it is convenient to call the attribute attribute names the same as the corresponding domains. The title of the relationship is:
Employees (Employee Number, Surname, Salary, Department Number)
Let at the moment the relation contains three tuples:
(1, Ivanov, 1000, 1)
(2, Petrov, 2000, 2)
(3, Sidorov, 3000, 1)
Such a relation is naturally presented as a table:
| Employee_number | Surname | Salary | Department_number |
|---|---|---|---|
| one | Ivanov | 1000 | one |
| 2 | Petrov | 2000 | 2 |
| 3 | Sidorov | 3000 | one |
Table 1 Employee Relations
Definition 3 . A relational database is a relationship set.
Definition 4 . A relational database schema is a set of relationship headers included in a database.
Although any relationship can be represented as a table, you need to clearly understand that relationships are not tables . These are close, but not identical concepts. Differences between relationships and tables will be discussed below.
The terms used by the relational data model have corresponding "tabular" synonyms:
| Relational term | Corresponding "tabular" term |
|---|---|
| Database | Table set |
| Database schema | A set of table headers |
| Attitude | Table |
| Title of relationship | Table header |
| Body relationship | Table body |
| Relationship attribute | Table column name |
| Relationship tuple | Table row |
| Degree (-ariness) of relationship | Number of table columns |
| Relationship power | Number of rows in the table |
| Domains and Data Types | Types of data in table cells |
Relationship properties follow directly from the above definition of a relationship. In these properties, the differences between relationships and tables mainly consist.
Remark It follows from the properties of a relation that not every table can define a relation. In order for a table to specify a relationship, it is necessary that the table has a simple structure (it would contain only rows and columns, and each row would have the same number of fields), the table should not have the same rows, any column of the table should contain data only one type, all used data types should be simple.
Remark Each relation can be considered an equivalence class of tables for which the following conditions are satisfied:
All such tables have different images of the same relationship.
The hardest thing is to define things that everyone understands. If you give not a strict, descriptive definition, then there is always the possibility of its incorrect interpretation. If we give a strict formal definition, then it is usually either trivial or too cumbersome. This is exactly the situation with the definition of the relationship in the First Normal Form ( 1NF ). It’s impossible not to talk about it at all, because на основе 1НФ строятся более высокие нормальные формы, которые рассматриваются далее в гл. 6 и 7. Дать определение 1НФ сложно ввиду его тривиальности. Поэтому, дадим просто несколько объяснений.
Объяснение 1 . Говорят, что отношение 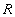находится в 1НФ, если оно удовлетворяет определению 2.
Это, собственно, тавтология, ведь из определения 2 следует, что других отношений не бывает. Действительно, определение 2 описывает, что является отношением, а что - нет, следовательно, отношений в непервой нормальной форме просто нет.
Объяснение 2 . Говорят, что отношение 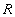находится в 1НФ, если его атрибуты содержат только скалярные (атомарные) значения.
Опять же, определение 2 опирается на понятие домена, а домены определены на простых типах данных.
Непервую нормальную форму можно получить, если допустить, что атрибуты отношения могут быть определены на сложных типах данных - массивах, структурах, или даже на других отношениях. Легко себе представить таблицу, у которой в некоторых ячейках содержатся массивы, в других ячейках - определенные пользователями сложные структуры, а в третьих ячейках - целые реляционные таблицы, которые в свою очередь могут содержать такие же сложные объекты. Именно такие возможности предоставляются некоторыми современными пост-реляционными и объектными СУБД.
Требование, что отношения должны содержать только данные простых типов, объясняет, почему отношения иногда называют плоскими таблицами ( plain table ). Действительно, таблицы, задающие отношения двумерны. Одно измерение задается списком столбцов, второе измерение задается списком строк. Пара координат (Номер строки, Номер столбца) однозначно идентифицирует ячейку таблицы и содержащееся в ней значение. Если же допустить, что в ячейке таблицы могут содержаться данные сложных типов (массивы, структуры, другие таблицы), то такая таблица будет уже не плоской. Например, если в ячейке таблицы содержится массив, то для обращения к элементу массива нужно знать три параметра (Номер строки, Номер столбца, номер элемента в массиве).
Thus, the third explanation of the First Normal Form appears:
Explanation 3 . The relation 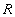is in 1NF if it is a flat table.
We consciously limit ourselves to considering only the classical relational theory, in which all relations have only atomic attributes and are obviously in 1NF.
The relational data model consists of three parts:
In the classical relational model, only simple (atomic) data types are used . Simple data types do not have an internal structure.
Domains are data types that have some meaning (semantics). Domains limit comparisons - it is incorrect, although it is possible, to compare values from different domains.
Attitude consists of two parts - the relationship header and the relationship body . The relationship header is an analogue of the table header. The title of the relationship consists of attributes. The number of attributes is called the degree of relationship . The relationship body is an analogue of the table body. The relation body consists of tuples . Relationship tuples are analogous to table rows. The number of relation tuples is called the ratio power .
The relationship has the following properties:
A relational database is a relationship set.
A relational database schema is a set of relationship headers included in a database.
The relation is in the First Normal Form ( 1NF ) if it contains only scalar (atomic) values.
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL