• The definition of an attribute on a set means that all values ​​must belong to this set. Restrictions - data values ​​(Salary - 0. 100).
• Logical constraints are a property that for a given set is true or false. Ivanov’s salary is higher than Petrova’s salary.
• Generalized restrictions - these restrictions apply to the set of objects, and not to a specific implementation. The salary of the head is more than the salary of the subordinate.

In addition to these restrictions, called external, there are internal restrictions - restrictions on the structure of the database.
If an attribute is a set, then duplication of values ​​is not allowed when entering information. Therefore, we need a language for describing constraints.
Restrictions are static and dynamic.
Static determine the state of the database.
Dynamic constraints determine the permissible database transitions from one state to another.

Restrictions for domains and attributes

Since attribute values ​​belong to domains, they inherit the properties and restrictions of these domains.

To change the property of inheritance it is necessary to differentiate the attributes. This is achieved by interpreting the domain and using abstraction techniques.
The usual way to semantize attributes is to use the technique of abstraction.
Suppose that between the attribute and the domain on which it is defined, there is another level of abstraction.
For example:

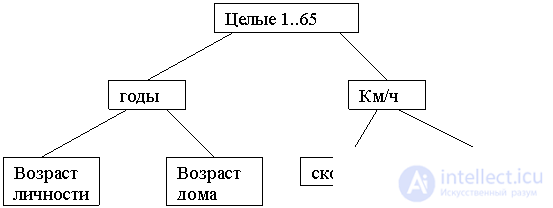
Interpreted domains, i.e., lower level domains, are associated with unit attributes.
Two attributes are not comparable if the domains associated with it cannot be reduced to a common associated domain.
You can enter not one, but several levels of associated domains, in order to ensure the accuracy of the semantic difference of attributes.
You can set limits for any associated domain by defining valid domain operations.
For example: age can be added and subtracted.
You can enter aggregate restrictions for all instances of this attribute.
For example: the sum of all staff salaries should not exceed a certain amount.

Constraints on entities and relationships

In data models (MD), restrictions can be set not only for attributes, but also for entity types and link types.
First of all, consider the class of restrictions defined on the mappings between attributes and / or types of entities.
A relationship is a mapping between two or more attribute sets and it is a subset of their Cartesian product.
Suppose there are two sets of attributes S1 and S2.
These two sets are defined as two mappings:
R: S1 -> S2 - display;
R1: S2 -> S1 is the inverse mapping.
The set S1 is the employee identification number, S2 is the name of the employee.
The coordinate number is the number of elements of the set S1 associated with the elements of the set S2.
If the relation has the record S1 (0,?) - then this means that any element in the set S2 can be associated with at least 0 and at most with? elements in S1.
The ratio S1 (0,?), S2 (0,?) Is the most common and has the name "many to many" or "M: N", that is, any element of the set S1 can be displayed on any number of elements of the set S2 and vice versa. By imposing certain restrictions on the minimum and maximum indicators, one can obtain various types of maps.
For example: Let S1 be the “Student” entity, and S2 the “exams” essence. Choose a relationship between these entities: Student passing (0,?) Exams (4, 6).
Thus, we have determined that any element of a student’s set must pass from 4 to 6 exams.
There are various kinds of constraints on relationships (relationships).
For example: R (S1 (0,?), S2 (1 ,?)) - describes that each element of the set S1 is mapped to one or more elements of S2, but any element of the set S2 is mapped to an arbitrary number of elements of the set S1.
This mapping is called a function .
R (S1 (0, 1), S2 (0,?)) - defines a functional mapping from S2 to S1, that is, any object in S2 is displayed by no more than one element from S1.
Example: Let the entity “Employee” have two attributes: “number” and “last name”. Each attribute is defined on its domain:
Number -> (101, 57, 85);
Surname -> (Ivanov, Petrov, Sidorov).
If there are no restrictions, then the extension of this intension may be the following:

Suppose there is a restriction: no employees have the same number. Then the extension is invalid and it is necessary to provide a functional mapping between the attributes “number” and “last name”, which is written in the form:
Number => last name.
This ratio is called “one to one”, that is, each and every element of S1 corresponds to one and only one element of S2, and vice versa.
There is one more kind of mappings “one to N" or "N to one" - "one to many".
For example: employees and departments in which they work.
There are full and partial mappings.
Partial mapping is a mapping when an element from the set S1 is mapped to 0 or more elements of the set S2, and an element from the set S2 to no more than one element of the set S1, but not for all elements of the set S2 this mapping is defined.
R (S1 (0, 1): S2 (0,?))
For example: each employee works in no more than one department, but not all departments have employees.
Full mapping is a mapping when each element of S2 is mapped by exactly one element of S1, and an element of S1 is mapped to 0 or more S2 elements.
For example: each employee must be assigned to any department.
There are a number of constraints that cannot be expressed as constraints on mappings.
For example: the salary of subordinates is less than the salary of the head.