Lecture
The third part of the relational model, the manipulation part, states that access to relational data is performed using relational algebra or equivalent relational calculus.
In implementations of specific relational DBMS, neither relational algebra nor relational calculus is currently used in its pure form. Structured Query Language (SQL) has become the de facto standard for accessing relational data. The SQL language is a mixture of relational algebra operators and relational calculus expressions using a syntax that is close to English phrases and enhanced by additional features not found in relational algebra and relational calculus. In general, a data access language is called relationally complete if it is not inferior in its expressive power to relational algebra (or, equivalently, to relational calculus), i.e. any operator of relational algebra can be expressed by means of this language. That's exactly what SQL is.
This chapter will cover the basics of relational algebra.
Relational algebra is a set of operators that use relations as arguments and return relations as a result. So the relational operator 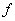 looks like a function with relations as arguments:
looks like a function with relations as arguments:
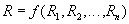
Relational algebra is closed because As arguments, you can substitute other relational operators of the following type into relational operators:
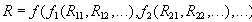
Thus, in relational expressions, you can use nested expressions of arbitrarily complex structure.
Each relationship must have a unique name within the database. The name of the relationship obtained as a result of a relational operation is defined in the left part of the equation. However, you can not require the presence of names from relations derived from relational expressions, if these relations are substituted as arguments in other relational expressions. Such relations will be called unnamed relations . Unnamed relationships do not really exist in the database, but are only calculated at the time of calculating the value of the relational operator.
Traditionally, following Codd [43], eight relational operators are defined, combined into two groups.
Set theoretic operators:
Special relational operators:
Not all of them are independent, i.e. Some of these operators can be expressed through other relational operators.
Some relational operators (for example, union) require that relations have the same headers. Indeed, the relationship consists of a heading and a body. The operation of combining two relations is simply the union of two sets of tuples taken from the bodies of the corresponding relations. But will the result be an attitude? First, if the initial relations have a different number of attributes, then it is obvious that the set, which is the union of such heterogeneous tuples, cannot be represented as a relation. Secondly, even if the relationship has the same number of attributes, but the attributes have different names. How then to determine the title of the relationship, resulting from the union of sets of tuples? Third, let relations have the same number of attributes, attributes have the same name, but are defined on different domains. Then again the union of the tuples will not form a relation.
Definition 1 . We will call relationships compatible by type if they have identical headings, namely,
Some relationships are not compatible by type, but become so after some renaming of attributes. In order for such relationships to be used in relational operators, an auxiliary attribute renaming operator is introduced.
The attribute renaming operator has the following syntax:
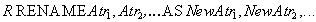
Where
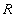 - attitude
- attitude
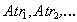 - the original attribute names,
- the original attribute names,
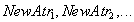 - new attribute names.
- new attribute names.
As a result of applying the attribute renaming operator, we get a new relationship, with the attribute names changed.
Example 1
The following statement returns an unnamed relationship in which the attribute 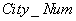 renamed to
renamed to 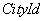 :
:
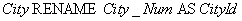
Definition 2 . Combining two compatible relationships  and
and  called a relationship with the same heading as the relationship
called a relationship with the same heading as the relationship  and
and  and body consisting of tuples belonging to or
and body consisting of tuples belonging to or  , or
, or  or both relationships.
or both relationships.
The syntax of the merge operation:
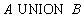
Remark A union, like any relation, cannot contain identical tuples. Therefore, if some tuple is included in  and attitude
and attitude  , it enters the union once.
, it enters the union once.
Example 2 Let two relationships be given  and
and  with employee information:
with employee information:
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
| 2 | Petrov | 2000 |
| 3 | Sidorov | 3000 |
Table 1 Attitude A
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
| 2 | Furs | 2500 |
| four | Sidorov | 3000 |
Table 2 Attitude B
Merging relationships  and
and  will look like:
will look like:
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
| 2 | Petrov | 2000 |
| 3 | Sidorov | 3000 |
| 2 | Pushnikov | 2500 |
| four | Sidorov | 3000 |
Table 3 Attitude A UNION B
Remark As can be seen from the above example, potential keys that were in a relationship  and
and  not inherited by combining these relationships. Therefore, in the union of relationships
not inherited by combining these relationships. Therefore, in the union of relationships  and
and  The attribute "Personnel Number" may contain duplicate values. If this were not the case, and the keys would be inherited, then this would contradict the notion of union as "union of sets". Of course, the union of relationships
The attribute "Personnel Number" may contain duplicate values. If this were not the case, and the keys would be inherited, then this would contradict the notion of union as "union of sets". Of course, the union of relationships  and
and  has, like any relationship, a potential key, for example, consisting of all attributes.
has, like any relationship, a potential key, for example, consisting of all attributes.
Definition 3 . The intersection of two compatible by type of relationship  and
and  called a relationship with the same heading as the relationship
called a relationship with the same heading as the relationship  and
and  , and the body, consisting of tuples belonging simultaneously to both relationships
, and the body, consisting of tuples belonging simultaneously to both relationships  and
and  .
.
Intersection operation syntax:
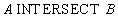
Example 3 For the same relationship  and
and  , as in the previous example, the intersection has the form:
, as in the previous example, the intersection has the form:
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
Table 4 Attitude A INTERSECT B
Remark It would seem that, unlike the union operation, the potential keys could be inherited by the intersection of relations. However, it is not. In general, no relational operators convey any data about potential keys to the resulting relation . The reason for this could be a trivial consideration that this is more simple and symmetrical - all operators are arranged in the same way. In fact, the reason is deeper, and lies in the fact that the potential key is a semantic concept that reflects the distinguishability of objects in the domain. The presence of potential keys is not derived from the structure of the relationship, but is explicitly defined for each relationship, based on its meaning. Relational operators are formal operations on relationships and are executed in the same way, regardless of the meaning of the data contained in the relationship. Therefore, relational operators cannot “know” anything about the meaning of data. The interpretation of the result of relational operations is the user's business.
Definition 4 . Subtracting two compatible relationships  and
and  called a relationship with the same heading as the relationship
called a relationship with the same heading as the relationship  and
and  , and body consisting of tuples belonging to the relation
, and body consisting of tuples belonging to the relation  and not belonging to the relation
and not belonging to the relation  .
.
Subtract operation syntax:
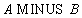
Example 4 For the same relationship  and
and  , as in the previous example, the subtraction is:
, as in the previous example, the subtraction is:
| Personnel Number | Surname | Salary |
|---|---|---|
| 2 | Petrov | 2000 |
| 3 | Sidorov | 3000 |
Table 5: A MINUS B Ratio
Definition 5 . Cartesian product of two relationships 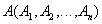 and
and 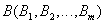 is called a relationship whose title is a concatenation of relationship headers
is called a relationship whose title is a concatenation of relationship headers  and
and  :
:
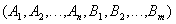 ,
,
and the body consists of tuples that are a concatenation of relations tuples  and
and  :
:
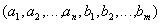 ,
,
such that 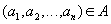 ,
, 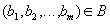 .
.
The syntax of a Cartesian product is:
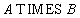
Remark Power of the work 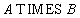 equal to the product of the power relations
equal to the product of the power relations  and
and  because every tuple relationship
because every tuple relationship  connects with every tuple relationship
connects with every tuple relationship  .
.
Remark If in a relationship  and
and  If there are attributes with the same name, then before performing the Cartesian product, such attributes must be renamed.
If there are attributes with the same name, then before performing the Cartesian product, such attributes must be renamed.
Remark You can multiply any two relationships, compatibility by type is not required.
Example 5 Let two relationships be given  and
and  with information about suppliers and details:
with information about suppliers and details:
| Vendor number | Supplier name |
|---|---|
| one | Ivanov |
| 2 | Petrov |
| 3 | Sidorov |
Table 6 Attitude A (Suppliers)
| Detail number | the name of detail |
|---|---|
| one | Bolt |
| 2 | Nut |
| 3 | Screw |
Table 7 Ratio B (Details)
Cartesian product of relationships  and
and  will look like:
will look like:
| Vendor number | Supplier name | Detail number | the name of detail |
|---|---|---|---|
| one | Ivanov | one | Bolt |
| one | Ivanov | 2 | Nut |
| one | Ivanov | 3 | Screw |
| 2 | Petrov | one | Bolt |
| 2 | Petrov | 2 | Nut |
| 2 | Petrov | 3 | Screw |
| 3 | Sidorov | one | Bolt |
| 3 | Sidorov | 2 | Nut |
| 3 | Sidorov | 3 | Screw |
Table 8: A TIMES B Ratio
Remark The Cartesian product operation itself is not very important, since she does not give any new information, compared with the original relationship. For real requests, this operation is almost never used. However, the operation of a Cartesian product is important for performing special relational operations, which will be discussed below.
Definition 6 . Sampling (restriction, selection) on the relationship  with the condition
with the condition 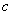 called a relationship with the same heading as the relationship
called a relationship with the same heading as the relationship  , and by the body consisting of tuples, the attribute values of which, when substituted into the condition
, and by the body consisting of tuples, the attribute values of which, when substituted into the condition 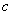 give the value TRUE.
give the value TRUE. 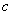 is a boolean expression that can include relationship attributes
is a boolean expression that can include relationship attributes  and (or) scalar expressions.
and (or) scalar expressions.
In the simplest case, the condition 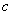 has the appearance
has the appearance 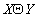 where
where 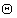 - one of the comparison operators (
- one of the comparison operators ( 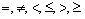 etc.), and
etc.), and 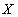 and
and 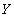 - relationship attributes
- relationship attributes  or scalar values. Such samples are called
or scalar values. Such samples are called  - selections ( theta sampling ) or
- selections ( theta sampling ) or  - restrictions
- restrictions 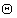 - selection .
- selection .
Sampling syntax:
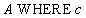 ,
,
or
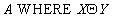
Example 6 Let given the relation  with employee information:
with employee information:
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
| 2 | Petrov | 2000 |
| 3 | Sidorov | 3000 |
Table 9 Ratio A
Sample result 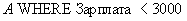 will look like:
will look like:
| Personnel Number | Surname | Salary |
|---|---|---|
| one | Ivanov | 1000 |
| 2 | Petrov | 2000 |
Table 10 Ratio A WHERE Salary <3000
The meaning of the sampling operation is obvious - choose tuples of a relation that satisfy a certain condition. Thus, the sampling operation gives a " horizontal slice " of the relationship for some condition.
Definition 7 . Relationship projection  by attributes
by attributes 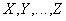 where each of the attributes belongs to the relation
where each of the attributes belongs to the relation  called the relationship with the title
called the relationship with the title 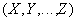 and body containing many tuples of view
and body containing many tuples of view 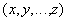 such for which
such for which  there are tuples with an attribute value
there are tuples with an attribute value 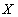 equal
equal 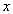 , attribute value
, attribute value 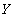 equal
equal 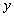 , ..., attribute value
, ..., attribute value 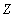 equal
equal 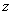 .
.
The projection operation syntax is:
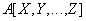
Remark The projection operation gives a " vertical cut " of the relationship, in which all duplicates of tuples arising from this cut are removed.
Example 7 Let given the relation  with information about suppliers, including name and location:
with information about suppliers, including name and location:
| Vendor number | Supplier name | Supplier City |
|---|---|---|
| one | Ivanov | Ufa |
| 2 | Petrov | Moscow |
| 3 | Sidorov | Moscow |
| four | Sidorov | Chelyabinsk |
Table 11 Attitude A (Suppliers)
Projection 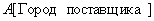 will look like:
will look like:
| Supplier City |
|---|
| Ufa |
| Moscow |
| Chelyabinsk |
Table 12 Attitude A [Supplier City]
The operation of connecting relations, along with the operations of sampling and projection, is one of the most important relational operations.
Usually, several types of join operations are considered:
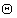 -connection (theta-compound)
-connection (theta-compound)The most important of these particular cases is the operation of a natural compound. All types of compounds are special cases of the general operation of the connection.
Definition 8 . Connection relationship  and
and  by condition
by condition 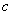 called attitude
called attitude
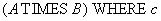
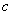 is a boolean expression that can include relationship attributes
is a boolean expression that can include relationship attributes  and
and  and (or) scalar expressions.
and (or) scalar expressions.
Thus, the join operation is the result of the sequential application of the Cartesian product and the sample operation. If in a relationship  and
and  If there are attributes with the same name, then such attributes must be renamed before making the connection.
If there are attributes with the same name, then such attributes must be renamed before making the connection.
Definition 9 . Let the attitude  contains an attribute
contains an attribute 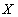 attitude
attitude  contains an attribute
contains an attribute 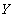 , but
, but 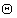 - one of the comparison operators (
- one of the comparison operators ( 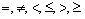 etc.). Then
etc.). Then 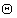 - connection of the relation
- connection of the relation  by attribute
by attribute 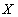 with attitude
with attitude  by attribute
by attribute 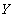 call attitude
call attitude
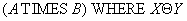
This is a special case of a generic join operation.
Sometimes, for surgery  -connections apply the following, shorter syntax:
-connections apply the following, shorter syntax:
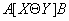
Example 8 Consider a company that stores data on suppliers and parts supplied. Let suppliers and parts assigned a status. Let the business of the company be organized in such a way that suppliers have the right to supply only those parts whose status is not higher than the status of the supplier (this may be that a good supplier with a high status can supply more types of parts, and a poor supplier with a low status can supply only a limited list of parts, the importance of which (the status of the part) is not very high).
| Vendor number | Supplier name | X
(Supplier Status) |
|---|---|---|
| one | Ivanov | four |
| 2 | Petrov | one |
| 3 | Sidorov | 2 |
Table 13 Attitude A (Suppliers)
| Detail number | the name of detail | Y
(Status details) |
|---|---|---|
| one | Bolt | 3 |
| 2 | Nut | 2 |
| 3 | Screw | one |
Table 14 Ratio B (Details)
The answer to the question "which suppliers have the right to supply what parts?" gives 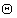 -connection
-connection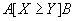 :
:
| Vendor number | Supplier name | X
(Supplier Status) |
Detail number | the name of detail | Y
(Status details) |
|---|---|---|---|---|---|
| one | Ivanov | four | one | Bolt | 3 |
| one | Ivanov | four | 2 | Nut | 2 |
| one | Ivanov | four | 3 | Screw | one |
| 2 | Petrov | one | 3 | Screw | one |
| 3 | Sidorov | 2 | 2 | Nut | 2 |
| 3 | Sidorov | 2 | 3 | Screw | one |
Table 15 Relationship "Which suppliers supply which parts"
The most important special case of a 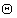 -connection is the case when
-connection is the case when 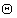 there is simply equality.
there is simply equality.
Equivalent syntax :
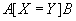
Example 9 Let there be relationships 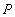 ,
, 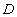 and
and 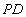 , storing information about suppliers, parts and deliveries, respectively (for convenience, we introduce the brief names of the attributes):
, storing information about suppliers, parts and deliveries, respectively (for convenience, we introduce the brief names of the attributes):
| Vendor number
PNUM |
Supplier name
PNAME |
|---|---|
| one | Ivanov |
| 2 | Petrov |
| 3 | Sidorov |
Table 16 P ratio (Suppliers)
| Detail number
DNUM |
the name of detail
DNAME |
|---|---|
| one | Bolt |
| 2 | Nut |
| 3 | Screw |
Table 17 Attitude D (Details)
| Vendor number
PNUM |
Detail number
DNUM |
Quantity supplied
VOLUME |
|---|---|---|
| one | one | 100 |
| one | 2 | 200 |
| one | 3 | 300 |
| 2 | one | 150 |
| 2 | 2 | 250 |
| 3 | one | 1000 |
Table 18 PD ratio (Supply)
The answer to the question, what parts are supplied by suppliers, gives equi-connection 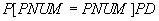 .In fact, because in a relationship there are identical attributes, then you must first rename the attributes, and then perform an equi-connection. Recording becomes more cumbersome:
.In fact, because in a relationship there are identical attributes, then you must first rename the attributes, and then perform an equi-connection. Recording becomes more cumbersome:
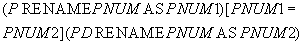
Usually, such a complex form of recording is not used. But be that as it may, the result is:
| Vendor number
PNUM1 |
Supplier name
PNAME |
Vendor number
PNUM2 |
Detail number
DNUM |
Quantity supplied
VOLUME |
|---|---|---|---|---|
| one | Ivanov | one | one | 100 |
| one | Ivanov | one | 2 | 200 |
| one | Ivanov | one | 3 | 300 |
| 2 | Petrov | 2 | one | 150 |
| 2 | Petrov | 2 | 2 | 250 |
| 3 | Sidorov | 3 | one | 1000 |
Table 19 Attitude "What parts are supplied by which suppliers"
The disadvantage of an equi-connection is that if a connection occurs by attributes with the same name (and most often it happens!), Then two attributes with the same values appear in the resulting relation. In our example, the attributes PNUM1 and PNUM2 contain duplicate data. You can get rid of this drawback by taking a projection on all attributes, except for one of the duplicates. This is how a natural connection works.
Definition 10 . Let given the relationship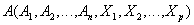 and
and 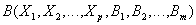 that have the same attributes
that have the same attributes 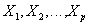 (i.e., attributes with the same name and defined on the same domains).
(i.e., attributes with the same name and defined on the same domains).
Then the natural mix of relationships and
and  called a relationship with a header
called a relationship with a header 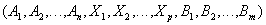 and a body containing many tuples
and a body containing many tuples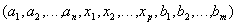 such that
such that 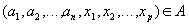 and
and 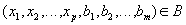 .
.
The natural connection is so important that a special syntax is used for it:
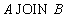
RemarkThe syntax of a natural connection does not indicate which attributes are being joined. A natural connection is made for all the same attributes.
Remark A natural connection is equivalent to the following sequence of relational operations:
Remark Можно выполнять последовательное естественное соединение нескольких отношений. Нетрудно проверить, что естественное соединение (как, впрочем, и соединение общего вида) обладает свойством ассоциативности , т.е.
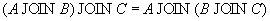
поэтому такие соединения можно записывать, опуская скобки:
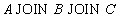
Пример 10 . В предыдущем примере ответ на вопрос "какие детали поставляются поставщиками", более просто записывается в виде естественного соединения трех отношений 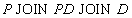 (для удобства просмотра порядок атрибутов изменен, это является допустимым по свойствам отношений):
(для удобства просмотра порядок атрибутов изменен, это является допустимым по свойствам отношений):
| Номер поставщика
PNUM |
Supplier name
PNAME |
Номер детали
DNUM |
the name of detail
DNAME |
Поставляемое количество
VOLUME |
|---|---|---|---|---|
| one | Ivanov | one | Болт | 100 |
| one | Ivanov | 2 | Nut | 200 |
| one | Ivanov | 3 | Screw | 300 |
| 2 | Петров | one | Болт | 150 |
| 2 | Петров | 2 | Nut | 250 |
| 3 | Сидоров | one | Болт | 1000 |
Table 20 P JOIN PD JOIN D ratio
Definition 11 . Let given the relationship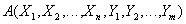 and
and 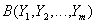 , and the attributes
, and the attributes 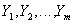 are common to the two relationships. The division of relationships
are common to the two relationships. The division of relationships  on
on 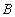 called a relationship with a header
called a relationship with a header 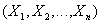 and a body containing a multitude of tuples
and a body containing a multitude of tuples 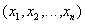 , such that for all tuples there is a tuple
, such that for all tuples there is a tuple 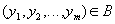 in relation to
in relation to
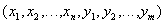 .
.
The relation  acts as a dividend , the relation
acts as a dividend , the relation 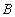 acts as a divider . Division of relations is similar to division of numbers with the remainder.
acts as a divider . Division of relations is similar to division of numbers with the remainder.
The syntax of the division operation:
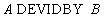
RemarkTypical inquiries implemented through a division operation usually have in their wording the word "all" - "which suppliers supply all the parts?".
Example 11In the example with suppliers, parts and deliveries, we answer the question "which suppliers supply all the parts?".
As a dividend, we take a projection 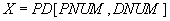 containing the numbers of the suppliers and the numbers of the parts supplied by them:
containing the numbers of the suppliers and the numbers of the parts supplied by them:
| Vendor number
PNUM |
Detail number
DNUM |
|---|---|
| one | one |
| one | 2 |
| one | 3 |
| 2 | one |
| 2 | 2 |
| 3 | one |
Table 21 Projection X = PD [PNUM, DNUM]
As a divider, take a projection 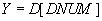 containing a list of the numbers of all parts (not necessarily supplied by someone):
containing a list of the numbers of all parts (not necessarily supplied by someone):
| Detail number
DNUM |
|---|
| one |
| 2 |
| 3 |
Table 22 Projection Y = D [DNUM]
Division 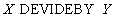 gives a list of vendor numbers that supply all parts:
gives a list of vendor numbers that supply all parts:
| Vendor number
PNUM |
|---|
| one |
Table 23 The ratio of X DEVIDEBY Y
It turned out that only supplier number 1 supplied all the parts.
Example 12 . Get the names of the vendors that supply part number 2.
Decision:
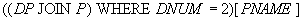
Example 13 . Get the names of suppliers supplying at least one nut.
Decision:
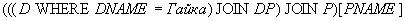
The answer to this request can be obtained in another way:
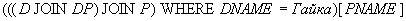
Example 14 Get the names of suppliers supplying all the details.
Decision:
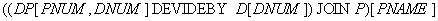
Example 15 Get the names of suppliers that do not supply part number 2.
Decision:
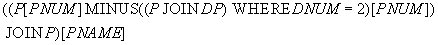
The answer to this request can be obtained step by step:
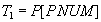 - get a list of numbers of all suppliers
- get a list of numbers of all suppliers
 - connect data on suppliers and supplies
- connect data on suppliers and supplies
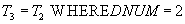 - in the data on suppliers and deliveries, leave only the data on deliveries of part number 2.
- in the data on suppliers and deliveries, leave only the data on deliveries of part number 2.
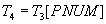 - get a list of vendor numbers that supply part number 2.
- get a list of vendor numbers that supply part number 2.
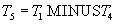 - get a list of supplier numbers that do not supply part number 2.
- get a list of supplier numbers that do not supply part number 2.
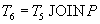 - connect the list of suppliers who do not supply part number 2 with data on suppliers (complete information will be obtained on suppliers who do not supply part number 2).
- connect the list of suppliers who do not supply part number 2 with data on suppliers (complete information will be obtained on suppliers who do not supply part number 2).
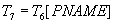 - the answer you are looking for (names of suppliers that do not supply part number 2).
- the answer you are looking for (names of suppliers that do not supply part number 2).
As stated at the beginning of the chapter, not all relational algebra operators are independent — some of them are expressed through other relational operators.
The join operator is defined in terms of the Cartesian product and the sample operator. For the natural join operator, a projection operator is added.
The intersection operator is expressed by subtracting as follows:
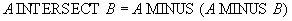
The division operator is expressed in terms of the subtraction, cartesian product and projection operators as follows:
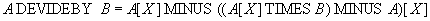
Thus, it is shown that join , intersection and division operators can be expressed through other relational operators, i.e. these operators are not primitive.
The remaining relational operators ( union , subtraction , Cartesian product , selection , projection ) are primitive operators - they cannot be expressed through each other.
The Cartesian product operator is the only operator that increases the number of attributes , so it cannot be expressed in terms of union, subtraction, selection, projection.
Оператор проекции - единственный оператор, уменьшающий количество атрибутов, поэтому его нельзя выразить через объединение, вычитание, декартово произведение, выборку.
Оператор выборки - единственный оператор, позволяющий проводить сравнения по атрибутам отношения, поэтому его нельзя выразить через объединение, вычитание, декартово произведение, проекцию.
Доказательство примитивности операторов объединения и вычитания более сложны и мы их здесь не приводим.
Несмотря на мощь языка реляционной алгебры, имеется ряд типов запросов, которые принципиально нельзя выразить только при помощи операторов реляционной алгебры. Это вовсе не означает, что ответы на эти запросы нельзя получить вообще. Просто, для получения ответов на подобные запросы приходится применять процедурные расширения реляционных языков.
Данный пример взят из книги Гилуа М.М. [6, стр.43].
Example 16 Пусть имеется отношение ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ с набором атрибутов (Наименование вещества, Водород, Гелий, …, 105_элемент). Значением атрибута "Вещество" являются наименования химических веществ, значениями остальных атрибутов - процентный состав соответствующих элементов в этом веществе. Такое отношение могло бы иметь, к примеру, следующий вид:
| Наименование вещества | Hydrogen | Helium | ... | 105 элемент |
|---|---|---|---|---|
| Дезоксирибону-клеиновая кислота | five | 3 | ... | 0.01 |
| Petrol | 50 | 0 | ... | 0 |
| ... | ... | ... | ... | ... |
Таблица 24 Отношение ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ
Рассмотрим запрос "Найти все химические элементы, содержание которых в каком-либо из веществ превышает заданный процент (скажем, 90)".
С алгоритмической точки зрения этот запрос выполняется элементарно - просматриваются все столбцы таблицы, если в столбце присутствует хотя бы одно значение, большее 90, то запоминается заголовок этого столбца. Набор наименований запомненных столбцов и является ответом на запрос.
Формально невозможно выразить этот запрос в рамках реляционной алгебры, т.к. ответом на этот запрос должен быть список атрибутов отношений, удовлетворяющих определенному условию. В реляционной алгебре нет операторов, манипулирующих с наименованиями атрибутов.
На самом деле, этот пример показывает, что таблица плохо нормализована (нормализация отношений рассматривается в гл.6 и 7). В таблице есть набор однотипных атрибутов ("Водород", "Гелий" и т.д. в количестве 105 столбцов).
Правильнее разбить это отношение на три различных отношения:
| НОМ_ВЕЩЕСТВА | ВЕЩЕСТВО |
|---|---|
| one | Deoxyribonucleic acid |
| 2 | Petrol |
Таблица 25 Отношение ВЕЩЕСТВО
| НОМ_ЭЛЕМЕНТА | ЭЛЕМЕНТ |
|---|---|
| one | Hydrogen |
| 2 | Helium |
| ... | ... |
| 105 | ... |
Таблица 26 Отношение ЭЛЕМЕНТЫ
| НОМ_ВЕЩЕСТВА | НОМ_ЭЛЕМЕНТА | ПРОЦЕНТ |
|---|---|---|
| one | one | five |
| one | 2 | 3 |
| one | 105 | 0.01 |
| 2 | one | 50 |
Таблица 27 Отношение ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ
Для отношений, нормализованных таким образом, исходный запрос реализуется следующей последовательностью операторов:
На языке SQL такой запрос реализуется одной командой:
SELECT ЭЛЕМЕНТЫ.ЭЛЕМЕНТ
FROM ЭЛЕМЕНТЫ, ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ
WHERE
ЭЛЕМЕНТЫ.НОМ_ЭЛЕМЕНТА=ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ.НОМ_ЭЛЕМЕНТА
AND ХИМИЧЕСКИЙ_СОСТАВ_ВЕЩЕСТВ.ПРОЦЕНТ>90 ;
Следующий пример иллюстрирует класс запросов, невыразимых средствами реляционной алгебры или реляционного исчисления по причине невыразимости средствами реляционной алгебры транзитивного замыкания отношений (см. гл. 1).
Пример 17 . Рассмотрим отношение, описывающее сотрудников некоего предприятия. Отношение содержит данные о табельном номере сотрудника, фамилии, должности и табельном номере руководителя сотрудника – СОТРУДНИКИ ( ТАБ_НОМ , ФАМИЛИЯ, ДОЛЖНОСТЬ, ТАБ_НОМ_РУК):
| ТАБ_НОМ | ФАМИЛИЯ | ДОЛЖНОСТЬ | ТАБ_НОМ_РУК |
|---|---|---|---|
| one | Ivanov | Директор | one |
| 2 | Петров | Глав.бухгалтер | one |
| 3 | Сидоров | Accountant | 2 |
| four | Vasiliev | Начальник цеха | one |
| five | Сухов | Master | four |
| 6 | Шарипов | Working | five |
| ... | ... | ... | ... |
Таблица 28 Отношение СОТРУДНИКИ
Рассмотрим запрос "Перечислить всех руководителей (прямых и непрямых) данного сотрудника".
Ответом на запрос может быть получен при помощи понятия транзитивного замыкания. Однако транзитивное замыкание не может быть выражено операторами реляционной алгебры.
Одной из задач, связанных с представлением табличных данных является построение так называемых кросс-таблиц.
Пусть имеется отношение с тремя атрибутами и потенциальным ключом, включающим первые два атрибута. Примером такого отношения могут быть данные с объемами продаж различных товаров за некоторые промежутки времени:
| Товар | Month | amount |
|---|---|---|
| Computers | January | 100 |
| Printers | January | 200 |
| Scanners | January | 300 |
| Computers | February | 150 |
| Printers | February | 250 |
| Scanners | February | 350 |
| ... | ... | ... |
Таблица 29 Данные о продажах
Требуется представить эти данные в виде таблицы, по строкам которой идут наименования товаров, по столбцам - месяцы, а в ячейках содержатся объемы продаж. Это и будет кросс-таблицей:
| Товар | January | February | ... |
|---|---|---|---|
| Computers | 100 | 150 | ... |
| Printers | 200 | 250 | ... |
| Scanners | 300 | 350 | ... |
Таблица 30 Кросс-таблица
Построение кросс-таблицы средствами реляционной алгебры невозможно, т.к. для этого требуется превратить данные в ячейках таблицы в наименования новых столбцов таблицы.
Доступ к реляционным данным возможен при помощи операторов реляционной алгебры. Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов, и возвращающие отношения в качестве результата. Реляционная алгебра замкнута таким образом, что результаты одних реляционных выражений можно использовать в других выражениях.
Традиционно определяют восемь реляционных операторов, объединенных в две группы.
Теоретико-множественные операторы: объединение , пересечение , вычитание , декартово произведение .
Специальные реляционные операторы: выборка , проекция , соединение , деление .
Для выполнения некоторых реляционных операторов требуется, чтобы отношения были совместимы по типу .
Не все операторы реляционной алгебры являются независимыми - некоторые из них выражаются через другие реляционные операторы. Операторы соединения , пересечения и деления можно выразить через другие реляционные операторы, т.е. эти операторы не являются примитивными. Оставшиеся реляционные операторы ( объединение , вычитание , декартово произведение , выборка , проекция ) являются примитивными операторами - их нельзя выразить друг через друга.
There are several types of queries that cannot be expressed by means of relational algebra. These include queries that require giving a list of attributes that satisfy certain conditions, building a transitive closure of relations, and building cross-tables. To get answers to such queries, you have to use procedural extensions of relational languages.
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL