Lecture
Это окончание невероятной информации про проектирование базы данных.
...
first given in 1971 by Heath.)
A relation is in Boyce-Codd normal form if and only if the determinants of each non-trivial and left irreducible functional dependence are potential keys of the relation .
Recall that the determinant is the left (defining) part of the functional dependence, and we call the trivial part of the functional dependence, in which the right (dependent) part is a subset of its left part (determinant).
That is, in the diagrams of functional dependencies of a relationship that is in the normal form of Beuys – Codd, the arrows pointing to these dependencies should come only from potential keys .
You can pay attention to the fact that the above definition of the Boyes-Kodd normal form does not use explicit references to the first , second and third normal forms, as well as to a transitive functional dependency, and from this point of view it is conceptually simpler. However, in practice, it is usually more simple to normalize relations by consistently transforming them from the first normal form to the second , and then into the third normal form and, if necessary, into the normal Boyes-Codd form .
We now consider the issues related to the normal form of Boyes-Codd in examples.
Example 1
Returning to the relation Exam in fig. 10.8, which is in the first and not in the second normal form, one can be sure that the relation is not in the NFBC. Indeed, its determinants are the simple attribute STANDS CODE and the composite attribute {STANDS CODE, Discipline}. Of these two determinants, only {STANDARD, DISCIPLINE} is the potential key of the relationship.
Example 2
The student_ hostel_Address ratio in Figure 10.12, which is in the second , but not in third normal form, is also not in the NFBK, since its determinants are the STUDENT_CODE attribute and the HOSTEL attribute, of which only the STUDENT CODE attribute is the key relationship.
Example 3
The STUDENTS and ACHIEVABILITY relationships presented in Figure 10.9, and the STUDENT_STABLISHING HOSTEL_ADDRESS relations in Figure 10.14, which, as we know, are in third normal form, are also found in the NFBC . Indeed, their determinants, namely the composite attribute {STANDARD CODE, DISCIPLINE} with respect to PERFORMANCE, the STANDARD CODE attribute in STUDENTS and STUDENT_STABLISHING attributes, the HOSTEL attribute in the HOSTAGE_Address, are at the same time the keys of these relations.
The given examples illustrate the fact that for relations in which there is only one potential key, finding a relationship in a third normal form is equivalent to finding it in a Boyes-Codd normal form .
Now consider examples of relationships in which there is more than one potential key , and then examples of relationships with overlapping composite potential keys.
Example 4
Consider a relation whose functional dependency diagram has the form shown in fig. 10.16.
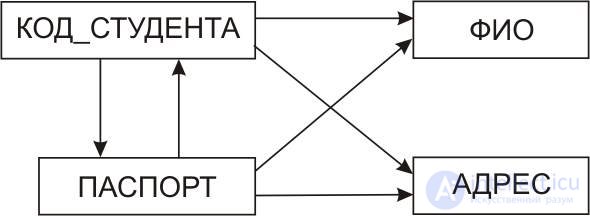
Fig.10.16. Functional dependency diagrams of a relationship with two potential keys
As can be seen from this diagram, this relation, unlike the ones considered earlier, has two potential keys. These are the attributes STANDING CODE and PASSPORT, from each of which all other attributes depend functionally. This relationship is in the second and third normal forms, since there are no irreducible left functional dependences of non-key attributes from potential keys and no transitive dependencies.
This relationship is also in the normal form of Boyce-Codd . Indeed, the determinants of this relationship are the attributes of the STUDENT CODE and the PASSPORT at the same time are its potential keys.
The given example illustrates the fact that the presence in itself with respect to several potential keys does not lead to the nonequivalence of the third normal form and the normal Boyes-Codd form .
And finally, pay attention to the following example.
Example 5
|
Let the following functional dependencies take place in this respect, shown in fig. 10.18.
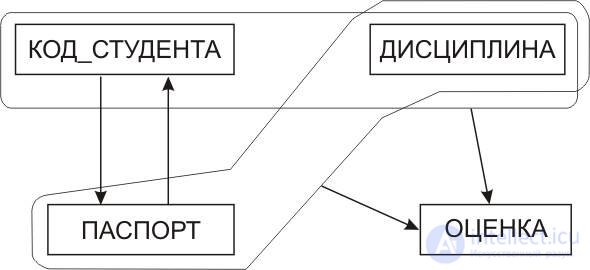
Fig.10.18. Functional Relationship Chart
As can be seen from these dependencies, the relationship has two potential keys. They are the composite attributes {STANDARD CODE, DISCIPLINE} and {PASSPORT, DISCIPLINE}. We draw attention to the fact that these keys are overlapping, since the attribute Discipline is part of both keys.
The relation presented is in third normal form, since its only non-key attribute, Evaluation depends on both keys irreducibly, and there are no transitive functional dependencies in relation to it.
However, this relationship is not in the NFBC. Indeed, it contains the determinants of the STANDING CODE and PASSPORT, which themselves are not potential keys, although they are part of them.
Referring to the example of the table in Figure 10.17, which represents this relationship, one can see the presence of redundant information in it: repeated identical pairs of values of the STANDER_CODE and PASSPORT. It is easy to understand that this redundancy leads to typical anomalies of data update operations:
The way out is the decomposition of the relationship in question into two relations.
|
|
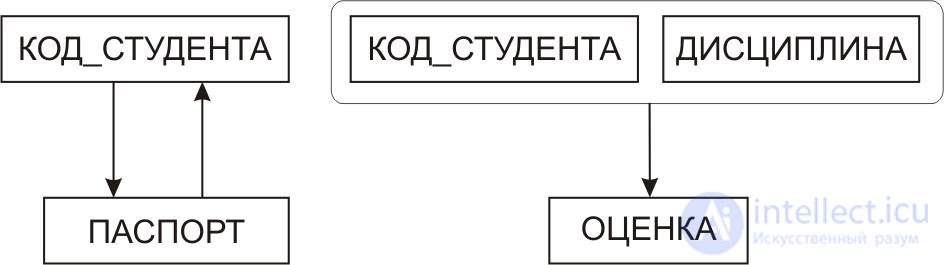
Fig.10.20. Diagrams of functional dependencies of relations in Figure 10.19.
Another option is possible decomposition, presented in Figure 10.21.
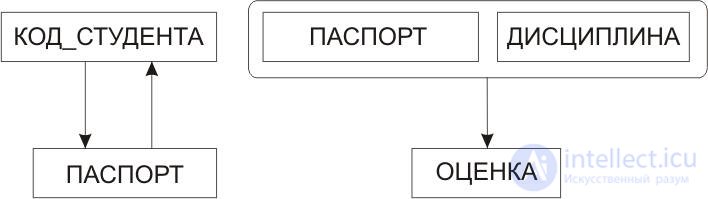
Fig.10.21. Another option is the decomposition of the relationship in ris.10.17
It is possible to make sure that each of the relations presented in Fig.10.19 - 10.21 is already in the normal form of Beuys - Codd, and there are no anomalies in the data updating operations.
Example 6
Let the relationship be given with the following set of attributes
{STUDENT CODE, Discipline, EVALUATION, TICKET NUMBER}.
The tuples of this relationship provide information that a particular student answers specific questions of a particular exam ticket when taking a particular discipline. At the same time there is a limitation that no two students can answer the same ticket for the same discipline. This restriction is equivalent to the following functional dependencies.
{STANDARD CODE, DISCIPLINE} → {TICKET NUMBER},
{DISCIPLINE, TICKET NUMBER} → {STUDENT CODE},
{STANDARD CODE, DISCIPLINE} → {EVALUATION},
{DISCIPLINE, TICKET NUMBER} → {EVALUATION}.
It can be seen that the relationship has two overlapping composite potential keys. These keys are the composite attributes {STANDARD CODE, DISCIPLINE} and {DISCIPLINE, BIBLE NUMBER}. In this case, it is not difficult to verify that the relation presented is in the normal form of Beuys - Codd, since all of its determinants are potential keys .
This example illustrates the fact that the mere existence of overlapping composite potential keys is not a sign that the ratio is not in the normal Boyes-Codd form.
The transformations of relations into the normal Boyes-Codd form discussed in the previous sections ensure the complete elimination of undesirable problems and anomalies of the INSERT , DELETE and UPDATE data updating operations, which are caused by the presence of functional dependencies between the attributes. For relationships in which only functional dependencies between attributes take place, bringing them to Boyes-Codd normal form ends the process of their normalization, since in this case the relation is already in the fourth and fifth normal forms. The problem, however, is that the dependencies between attributes are not limited to functional dependencies only. In addition to functional relationships , there may be other, more complex, types of dependencies between attributes. Thus, the introduction of the fourth normal form considered in this section is connected with the need to solve problems caused by the presence of a so-called multi - valued dependence.
Consider as an example the relationship presented in Figure 10.22.
|
It is clearly seen that the relation STUD_KURS_DISTS, shown in Figure 10.22, suffers from redundancy and the associated anomalies of update operations. In this respect, between the attributes {STUDENT, COURSE, DISCIPLINE} there are only trivial functional dependencies of the type {STUDENT, COURSE, DISCIPLINE} → {DISCIPLINE} or {STUDENT, COURSE, DISCIPLINE} → {STUDENT, COURSE}, etc. Primary key This relationship is a set of attributes {STUDENT, COURSE, DISCIPLINE}, that is, the whole tuple of this relationship. Considering the materials of the previous sections, it is easy to see that this relationship is already in the normal form of Beuys - Codd, since the only determinant of the relationship {STUDENT, COURSE, DISCIPLINE} is at the same time its key. Therefore, in this respect, by definition, there should be no problems associated with functional dependence. However, it is also clearly seen that this relationship, however, clearly suffers from the presence of anomalies of data update operations. Indeed, to add, for example, information about a new discipline in a particular course, we must add tuples with this discipline for each student enrolled in this course.
The relationship problems presented in Figure 10.22 are no longer related to functional dependency, but to the presence in it of a so-called multivalued dependency connecting the attribute course with student attributes and discipline. This dependence consists in the fact that the specific value of the attribute of the course uniquely determines not one, but the set of the corresponding attribute values of the student and the discipline, namely the set of students enrolled in this course. At the same time, the values of student and discipline attributes are completely independent of each other.
Figure 10.23 explains the nature of the dependencies between the attributes in this example, when the course attribute values uniquely determine not the individual values of the student attributes and discipline, but specific sets of values, namely the set of students enrolled in a particular course and the set of disciplines studied by each student of a particular course.
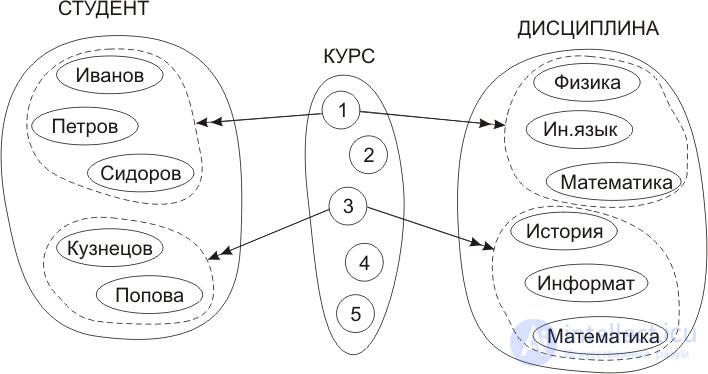
Fig.10.23. Illustration of multi-valued dependencies
Multiple dependency is indicated by a double arrow as follows:
COURSE → [GO] TOURISM and COURSE → [AGREEMENT).
A → → B means that the attribute B is multi-valued depends on the attribute A , or the attribute A multi-valuedly determines the values of the attribute B.
Placing in the same table information about the elements of two subsets of attribute values student and discipline for each attribute value course leads to the multiplication of relationship tuples because of the need to specify all combinations of elements of subsets of attribute values student and discipline related to a specific attribute attribute course.
The definition of a multi-valued dependence is as follows.
Let A, B and C be arbitrary subsets of the attribute set of the relation R. Then B depends significantly on A, i.e. A → → B, if and only if the set of values of B corresponding to a given pair {value A, value C} relations R, depends on A, but does not depend on C.
The independence of the set of values of B from the values of C means that a specific value of A and the set of values of B determined by it can occur for any value of the attribute C.
It can be shown that for a given relation R { A , B , C } a multi-valued dependence A → → D B is fulfilled if and only if the dependence A → T is also fulfilled. In other words, multi-valued dependencies in relation always form connected pairs , and therefore they are usually presented in a symbolic form together: A → → → → B and A → → → → D, or shorter - A → → → B | C.
For the example in question, this entry has the following form:
COURSE → [GO] DISCIPLINE.
If we again refer to the functional dependency considered earlier, it is easy to see that in fact the functional dependency is a special case of a multivalued dependency , namely, the case when the set of dependent values corresponding to specific determinant values is always a one-element set.
Thus, it can be said that the problems of the relation under consideration (Figure 10.22) are related to the fact that it contains multi-valued dependencies that are not functional .
The problems of this relationship are solved by its decomposition into two projections.
|
|
The possibility of such a decomposition is justified by the Feigin theorem.
Feigin's theorem.
Let A, B and C be sets of attributes of the relation R {A, B, C}. The relation R will be equal to the combination of its projections {A, B} and {A, C} if and only if for the relation R the multi-valued dependence A → → is true B.
You can pay attention to the fact that the Feigin theorem is a generalization considered in Section 10.3 of the Hez theorem, which, recall, sounds like this.
Hez's theorem.
Let R {A, B, C} be a relation, where A, B and C are attributes of this relation. If R satisfies the dependences A ® B, then R is equal to the connection of its projections {A, B} and {A, C}.
As can be seen, the Hez theorem follows naturally from the Feigin theorem.
Now we can define the fourth normal form of the relation.
The relation R is in the fourth normal form (4NF) if and only if there are subsets A and B of the attributes of the relation R such that the non-trivial multivalued dependence A → → D B and all attributes R also functionally depend on A.
The above strict definition of the fourth normal form requires clarification. The last condition, consisting in the fact that all attributes of the relation R are also functionally dependent on A , means that A is the potential key of the relation. In this case, the multi-valued relationship A → key B is actually degenerate , that is, presented in this respect as a functional relationship. In other words, nontrivial multivalued dependences are present in relation to R only in the form K → X , that is, the attribute X functionally depends on the primary key K.
Even easier, this definition can be formulated as follows.
The relation R is in the fourth normal form if it is in the Boyes – Codd normal form, and all the multi-valued dependencies of the relation R are functional dependencies on potential keys .
Приведенное определение четвертой нормальной формы не следует истолковывать таким образом, что при декомпозиции отношения с многозначными зависимостями именно эти зависимости становятся функциональными. Выше уже говорилось, что многозначные зависимости могут существовать только парами и при декомпозиции отношения эти пары разрываются и сами многозначные зависимости исчезают .
И, наконец, на случай наличия в отношении многозначных зависимостей может быть обобщено приведенное ранее в разделе 10.5 определение Риссанена, касающееся декомпозиции отношения на независимыепроекции. Оно имело следующий смысл.
Отношение R{А, В, С}, удовлетворяющее функциональным зависимостям А→В, следует разбивать напроекции {А, В} и {А, С}.
То же самое можно утверждать и для многозначных зависимостей А →→ В , то есть
отношение R{А, В, С}, удовлетворяющее многозначным зависимостям
А →→ В|С, следует разбивать на проекции {А, В} и {А, С}.
В предыдущих разделах, посвященных вопросам нормализации отношений, рассматриваются случаи, когда единственно необходимой и допустимой операцией для устранения имеющих место в отношениях проблем является декомпозиция без потерь отношения на две его проекции. Такая декомпозиция решала проблемы, связанные с наличием в отношении многозначной зависимости и ее частного случая – функциональной зависимости, и на такой декомпозиции основывается последовательная нормализация отношений от первой нормальной формы до четвертой.
Однако, возможны случаи, когда устранение в отношении аномалий не может быть достигнуто путем декомпозиции отношения на две его проекции без потерь, в то время как декомпозиция его на три и более проекций обеспечивает отсутствие потерь информации и устранение аномалий. Другими словами, для некоторых отношений возможна декомпозиция без потерь на n проекций, а на меньшее число проекцийдекомпозиция без потерь невозможна.
Рассмотрим в качестве примера отношение, имеющее следующий набор атрибутов {СТУДЕНТ,ДИСЦИПЛИНА, ПРЕПОДАВАТЕЛЬ}. В этом отношении представлена информация о студентах, изучающих конкретные дисциплины у конкретных преподавателей. При этом каждый студент изучает несколько дисциплин, каждый преподаватель может преподавать несколько дисциплин и студент может обучаться у нескольких преподавателей. Ключом такого отношения является составной атрибут {СТУДЕНТ,ДИСЦИПЛИНА, ПРЕПОДАВАТЕЛЬ}, то есть весь кортеж отношения. Это отношение не содержит нетривиальных функциональных и многозначных зависимостей и поэтому полностью удовлетворяет требованиям четвертой нормальной формы .
Теперь допустим, что в отношении имеются следующие кортежи: кортеж, в котором представлена информация о том, что студент Иванов изучает Физику, другой кортеж, в котором указано, что преподаватель Степанов преподает Физику, и третий кортеж, в котором указано, что преподавательСтепанов обучает студента Иванова. Пример фрагмента такого отношения представлен на рис. 10.25.
|
В общем случае из трех описываемых этими кортежами фактов совсем не обязательно должно следовать, что студент Иванов изучает Физику именно у преподавателя Степанова. Тем не менее, предположим, что в нашей предметной области имеет место такое правило, определяющее, что из наличия указанных трех фактов обязательно следует, что студент Иванов должен изучать Физику у преподавателя Степанова. При этом, вообще говоря, преподавателю Степанову не запрещено преподавать другие дисциплины, а студентуИванову изучать Физику и у другого преподавателя.
Это ограничение целостности формально можно сформулировать следующим образом.
Если в каких-либо кортежах отношения R имеются пары значений атрибутов (С1, Д1), (Д1, П1) и (П1, С1), или, что эквивалентно, если в отношении присутствуют кортежи { С1 , Д1 , П2 }, { С2 , Д1 , П1 } и { С1 , Д2 , П1 }, то в этом отношении обязательно также должен быть кортеж вида { С1 , Д1 , П1 }.
Такого вида ограничение называют циклическим , или 3Д - ограничением .
Пример отношения, удовлетворяющего такому ограничению целостности, приведен на рис. 10.26.
|
Рис.10.26. Отношение СТУД_ДИСЦ_ПРЕП
Можно заметить, что следствием рассматриваемого циклического или 3Д -ограничения является то, что каждая пара значений атрибутов обязательно должна встречаться в двух экземплярах в разных кортежах. Из-за этого в данном отношении появляются проблемы при выполнении в нем операций обновления данных в кортеже – INSERT , DELETE и UPDATE , так как каждая из этих операций, может затрагивать не один, а большее число кортежей.
Например, если в отношение
|
вставить кортеж {Петров, Физика, Степанов}, то для выполнения 3Д -ограничения также должен быть вставлен и кортеж {Иванов, Физика, Степанов}, так как к уже имеющимся в отношении парам (Иванов, Физика) и (Иванов, Степанов) добавляется третья пара (Физика, Степанов).
Another example.
Пусть из отношения
|
Если же требуется удалить кортеж {Иванов, Физика, Степанов}, то для каждой его пары (Иванов, Физика), (Физика, Степанов) и (Иванов, Степанов) имеются двойники в других кортежах. Следовательно, для того чтобы требования 3Д -ограничения не нарушились, вместе с кортежем {Иванов, Физика, Степанов} должен быть удален и какой-либо из кортежей с парой-двойником. Возникает только вопрос, какой из трех кортежей должен быть также удален.
Указанные проблемы операций обновления, обусловленные наличием 3Д -ограничения, могут быть решены путем замены рассматриваемого отношения СТУД_ДИСЦ_ПРЕП (рис.10.25, 10.26) тремя его бинарными проекциями СТУД_ДИСЦ, ДИСЦ_ПРЕП и СТУД_ПРЕП, как это показано на рис. 10.27
|
|
|
Возникает вопрос, почему необходима декомпозиция на три , а не на два отношения. Можно, однако, увидеть, что соединение любых двух из этих отношений не обеспечивает восстановления исходногоотношения. Например, результатом соединения отношений СТУД_ДИСЦ и ДИСЦ_ПРЕП по атрибутуДИСЦИПЛИНА будет отношение, представленное на рис. 10.28.
|
Видно, что это отношение не совпадает с исходным отношением СТУД_ДИСЦ_ПРЕП (рис. 10.26). В нем имеется лишний кортеж {Петров, Физика, Кузнецов}, которого не было в отношенииСТУД_ДИСЦ_ПРЕП. Если же еще выполнить соединение этого отношения (рис.10.28) с третьим отношениемСТУД_ПРЕП (рис.10.27) по атрибутам Студент и Преподаватель, то нетрудно увидеть, что лишний кортеж будет исключен и исходное отношение СТУД_ДИСЦ_ПРЕП будет полностью восстановлено.
Поскольку рассматриваемое 3Д -ограничение удовлетворяется тогда и только тогда, когда отношение равносильно соединению трех его проекций, такое ограничение еще называют зависимостью соединения (или зависимостью проекции-соединения ).
Зависимость соединения ( join dependency ) является таким же семантическим ограничением данногоотношения, как многозначная и функциональная зависимости. Определение зависимости соединения имеет следующий вид.
Пусть R является отношением, а А, В, …, Z – произвольным подмножеством множества атрибутовотношения R. Отношение R удовлетворяет зависимости соединения *(А, В, …, Z) тогда и только тогда, когда оно равносильно соединению своих проекций с подмножествами атрибутов А, В, …, Z.
Таким образом, для рассматриваемого в этом разделе отношения СТУД_ДИСЦ_ПРЕП (рис. 10.26) можно записать, что оно удовлетворяет зависимости соединения *(СТУД_ДИСЦ, ДИСЦ_ПРЕП, СТУД_ПРЕП) и для устранения аномалий операций обновления может быть представлено своими тремя проекциями {СТУДЕНТ, ДИСЦИПЛИНА}, {ДИСЦИПЛИНА, ПРЕПОДАВАТЕЛЬ} и {СТУДЕНТ, ПРЕПОДАВАТЕЛЬ}.
Сравним приведенные определения зависимости соединения с рассмотренной выше теоремой Фейгина.
Отношение R{А, В, С} может быть декомпозировано без потерь на проекции с атрибутами {А, В} и {А, С}тогда и только тогда, когда для отношения R выполняются многозначные зависимости А →→ В (и А →→С).
Можно видеть, что фактически многозначная зависимость А →→ В эквивалентна (является частным случаем) зависимости соединения *( АВ , АС ).
Другими словами, зависимость соединения является обобщением многозначной зависимости, так же, как ранее многозначная зависимость оказалась обобщением функциональной зависимости. И наоборот,многозначная зависимость является частным случаем зависимости соединения, а функциональная зависимость – частным случаем многозначной зависимости.
Таким образом, мы выяснили, что отношение может находиться в четвертой нормальной форме , но, тем не менее, у него могут быть проблемы операций обновления, связанные с наличием в нем зависимости соединения, не являющейся многозначной зависимостью (в четвертой нормальной форме многозначные зависимости отсутствуют). Эти проблемы могут быть решены путем декомпозиции отношения на три или большее число его проекций. Тем самым отношение приводится к, так называемой, пятой нормальной форме . Дадим ее определение.
Определение пятой нормальной формы .
Отношение R находится в пятой нормальной форме (5НФ), которая также называется проекционно-соединительной нормальной формой , тогда и только тогда, когда каждая зависимость соединения в отношении R подразумевается потенциальными ключами отношения R.
Другими словами, в отношении присутствуют только функциональные зависимости атрибутов отпотенциальных ключей.
Пятая нормальная форма является окончательной нормальной формой по отношению к операциямпроекции и соединения.
Рассмотренные в предыдущих разделах материалы по нормализации отношений путем их декомпозиции без потерь с целью устранения нежелательных проблем при выполнении операций обновления данных можно свести к последовательности этапов, обеспечивающих пошаговое преобразование отношений в нормальные формы вплоть до пятой нормальной формы .
Эти этапы формулируются следующим образом.
При этом важно то, что декомпозиция отношений на проекции должна осуществляться без потерь и с сохранением зависимостей .
Можно обратить внимание на предложенные Фейгином интересные альтернативные определения нормальной формы Бойса – Кодда , четвертой нормальной формы и пятой нормальной формы .
Отношение R находится в нормальной форме Бойса – Кодда тогда и только тогда, когда каждаяфункциональная зависимость подразумевается потенциальными ключами отношения R .
Отношение R находится в четвертой нормальной форме тогда и только тогда, когда каждаямногозначная зависимость подразумевается потенциальными ключами отношения R .
Отношение R находится в пятой нормальной форме тогда и только тогда, когда каждая зависимость соединения подразумевается потенциальными ключами отношения R .
Часть 1 Database Design
Часть 2 10.7 Multiple dependencies and fourth normal form - Database Design
Comments
To leave a comment
Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL
Terms: Databases, knowledge and data warehousing. Big data, DBMS and SQL and noSQL