2.2 The second law of thermodynamics. Entropy

We draw attention to the extremely important circumstance, namely, the role of the refrigerator. Each engine must have its own refrigerator, and at a certain stage of the cycle, this refrigerator must be given some of its energy. This, in essence, is the second law of thermodynamics. In other words, there seems to be a kind of fundamental "tax": nature recognizes the equivalence of heat and work, but it requires a "contribution" from us whenever heat is converted into work. But there is also asymmetry: nature does not impose a “tax” on the conversion of work into heat, for example, through friction.

The second law of thermodynamics has different formulations, for example,

Carnot : "The greatest efficiency of a heat engine does not depend on the working fluid and is determined only by the temperature within which the engine runs."

Clausius : "Heat cannot pass from a cold body to a warm one by itself, by the free way."

We draw attention to the common phenomena of nature and life from the position of the second law of thermodynamics.

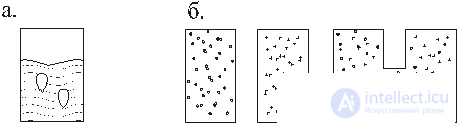
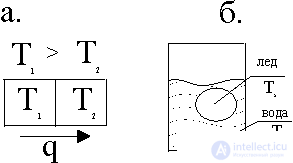
In fig. 1, and a vessel with a cocktail 1 is shown with a temperature T ₁ and ice 2 with a temperature T ₂ , the ice will melt and the average temperature T ₁ > T _cf > T _{2 will be established} .

In fig. 1, b there are different gases in two vessels; when vessels are connected, the gas distribution is set to be uniform and the same in them. If there is a drop of gasoline in a puddle, then it eventually spreads over the surface. The following observations also belong to this class: the cigarette smoke ring is melting; fire is extinguished and so on.

It follows from these observations that the tendency towards the dispersion of energy, equalization of temperatures, concentrations, and pressures prevails in nature. In this case, the state of matter changes in a single direction - the alignment of various gradients.

Hence the idea of ​​the thermal death of the universe. As an astronomer Jeans wrote: "Nothing remains but boring uniformity, from which only small and minor local changes can be expected."

The state of uniformity is, as it were, the most probable, which made it possible to give another formulation to the second beginning

Boltzmann : "Nature tends to transition from less likely states to more likely states."

It turned out that these processes can be expressed quantitatively. To characterize the thermal state of the system, Clausius introduced in 1865 a new quantity — entropy ^* . According to the Greek word 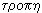means "conversion", "rotation", and entropy - 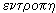- "transform", "cycle".

More quantitative definition, entropy output is given in a separate paragraph.

Entropy is a parameter that determines the state of the system, in particular, gas, and is a function of this state, as well as pressure P, volume V, temperature T, internal energy U, i.e., macroscopic parameter.

Further, it will be shown that entropy determines the state of the system from the standpoint of its internal ordering: the greater the chaos in the system, the higher its entropy. Generalizing these properties, Clausius formulated the law: "The energy of the Universe is constant, the entropy of the Universe tends to the maximum."

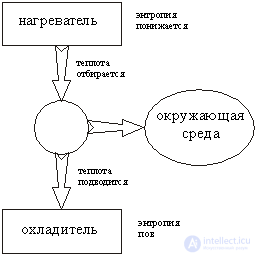
In fig. 2 shows the scheme of the work of converting thermal energy into work: thermal energy is transferred from the heater to the machine, which turns it into work. In this case, nature is paid a "tax" in the form of heat, reported to the refrigerator. This energy is already unsuitable for work, if you do not use even more "cold" refrigerator. The energy stored at a higher temperature, has a higher "quality": it is suitable for work. Let's look at these processes from the position of entropy change.

When the energy Q ₁ is transferred from the heater to the refrigerator, the entropy decreases by Q ₁ / T ₁ and simultaneously increases by Q ₂ / T ₂ . Entropy characterizes the conditions under which energy is stored: if energy is stored at a high temperature T ₁ , then its entropy is low and qualitatively high.

The natural course of change processes is characterized by a decrease in the energy quality of the Universe. Since the energy of the Universe remains constant (the first law of thermodynamics), when burning fuel (coal, oil, uranium, etc.), the total energy reserves do not change, but the world’s entropy increases. In other words, it is necessary to direct the development of civilization along the path of reducing the level of entropy production.

The second law of thermodynamics speaks only of the direction of change of magnitudes: the entropy grows. Consider the following example: two bodies are brought into contact with temperatures T ₁ and, T ₂ transfers heat flow from the first to the second body. This process is carried out during the melting of ice in a vessel with water (Fig. 3). In this case, the water gives the ice energy 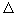Q and its entropy S _in falls on 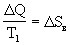<0. Ice gets energy 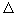Q and its entropy 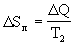> 0 increases. Total entropy change:

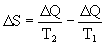> 0

This process is irreversible, and in the water-ice system the entropy increases. The question arises: to what value can entropy grow? The answer is obvious - to S = S _max , at which an equilibrium state occurs.

If these conclusions are extended to the Universe, then it is expected to complete alignment of the gradients of all parameters in nature, i.e., thermal death.

Throughout Newtonian physics until the XIX century, they dealt only with reversible processes. Indeed, the second law of mechanics can be represented in the form

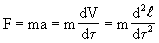
where time appears in a square, i.e. it is possible to turn the process into the past (-t). But if we take into account the transformation of a part of mechanical energy into heat due to friction, then the friction force F _Tr , as is known, is proportional to the normal component of the velocity gradient, i.e.

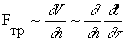
In this case, replacing the positive time direction t with the opposite (-t) will result in a change in the results. When energy dissipation is taken into account, invariance with respect to time disappears, i.e. the process becomes asymmetric.

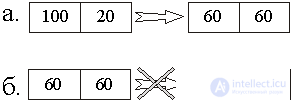
This is manifested in all thermal processes. For example, in fig. 4, a shows the process of equalizing the temperatures of the two bodies brought into contact with the initial temperatures T ₁ = 100 ^o and T ₂ = 20 ^o But the reverse process (Fig. 4, b) is prohibited.

So classical physics stumbled over the "stone" of entropy. This conflict was attempted by the Austrian physicist Boltzmann. He viewed gas as an ensemble of a huge number of moving molecules. The erratic movement of molecules in a gas is a thermal movement. The higher the velocity of the molecules, the higher the temperature of the gas, which can be expressed in terms of statistically averaged velocities. This can be done for entropy.

So Boltzmann managed to get a strict interpretation for entropy in terms of Newtonian physics. At the same time, Boltzmann gave a physical explanation of the concept of "growth of entropy": the growth of entropy - the growth of chaos - the destruction of order. But this work will be discussed below.

Let us compare two most important parameters in physics - entropy and energy. In a gigantic factory of natural processes, the principle of entropy can be compared with the role of a director who prescribes transactions, and the law of conservation of energy plays the role of a chief accountant who balances debit and credit. In an isolated system, the processes go so that 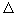S> 0.

Let us pay attention to one more feature of entropy: in reversible processes, entropy, like energy, is conserved, and in irreversible ones, energy is conserved, and entropy grows until an equilibrium state occurs. If the development of natural processes is characterized by the growth of entropy, then the movement of time (the so-called "arrow of time") should also be directed from the past to the future.

In the previous arguments, it was implicitly assumed that the reversible process proceeds infinitely slowly, because at each stage, at least when analyzing the Carnot cycle, there is an equilibrium. The gas temperature T _g is equal to the temperature T _{x of the} cooler, T _g = T _x . In the argument there is no concept of speed of the process, time. This peculiarity of considering processes allows one to call classical thermodynamics more correctly thermostatics. In the future, time will be introduced into the reasoning, and this will take the first step towards genuine thermodynamics.