7.3 Mandelbrot Set

Above, one of the ways to construct fractals was considered - sequential operations of constructing similar elements. We now turn to the fractals arising according to the scheme from §7.1.

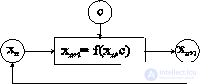
Fig. 1 Schematic diagram of the dynamic process _{xn + 1} = f ( _xn , C)

In 1980, Benoit Mandelbrot discovered the universal set, now bearing his name. Mandelbrot instead of real numbers considered complex and watched the process x ₀ x ₁ x _{2 is} not on a line, but in a plane. Mandelbrot process is carried out according to the formula

x _{n + 1} = f (x _n ) = x _n + C, C = a + bi,

that is, choose an arbitrary number x ₀ , square it, add the constant C, and get x ₁ ; then repeat for x ₂ , x ₃ , etc.

Put C = 0, then x ₀ x ₀ ² x ₀ ⁴ x ₀ ⁸ and this sequence has three possibilities:

• the numbers are getting smaller and their sequence tends to zero, i.e. null becomes an attractor for process x x 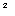. All points lying at a distance less than 1 from the attractor move to it.
• the numbers are getting bigger and tend to infinity, which is an attractor for this process. All points lying at a distance greater than 1 from zero go to infinity.
• the points are at a distance of 1 from zero, their sequences form a circle of unit radius.

The plane is divided into two zones of influence, and the border is a circle.

Surprises start when we choose a non-zero value C = a + bi. The following is a set of Mandelbrot (MM) for process x x 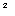+ C, where part of the complex C-region is shown: - 2.25 C <1.5. The figure reflects the correspondence to different values ​​of the parameter C of different types of borders on the complex C-plane. Denote by black the range of values ​​of C, where the sequence is limited, and white is the exponential divergence.

Fig. 2 The Mandelbrot set and its enlarged fragment "in its pure form"

It can be seen that with the exit to the complex plane we get a more complete picture compared with the analysis on the real axis. A different choice of the complex number C leads to a variety of configurations. In a simple black and white image you cannot see such a wealth of forms. A complex dynamic structure can only be reflected in color.

Fig. 3 Equipotential surfaces around the Mandelbrot set.

We describe how coloring of a neighborhood of MM occurs. Let the set be made of metal and carry an electric charge, then the surface has a constant electric potential, for example, 1000 V. In the area surrounding the conductor, the potential drops to zero. You can build equipotential lines surrounding the MM. For example, the line corresponding to the potential of 1 V is so far from MM that it looks almost like a circle, and the line 900 V resembles the shape of MM, etc. The coloring of the pictures corresponds to these lines: different colors give a contour map of the electrostatic potential between MM and infinity. Another fractal is closely connected with MM - Julia's set.

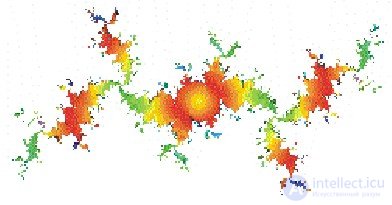
Fig. 4 Julia set

If in ММ Х ₀ = const = 0, and the parameter С is the complex coordinate of the point on which the construction is performed; then in the Julia set C = const, set in advance, and the construction plane is the plane of possible initial values ​​X ₀ . There are many programs that build the fractals in question, more about this can be found on the authors home page, and here we offer a "small" (520Kb) collection of pictures. Hard to believe but formula 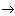x x + C contains a lot of structures. The multitude of MM itself manifests itself again and again, of various sizes, but always of the same form. It resembles the genetic organization of higher organisms: each cell contains a complete genome, a collection of all forms of manifestation, but at any point in the body only some small part of these forms appear.