The definition of information on Shannon and the methods of its evaluation, which came from probability theory, are given. Considered on a specific example, the evaluation of information in the text. The definitions of information redundancy, the coefficient of stochasticity, the optimal ratio between determinism and stochasticity are introduced. The application of the stochasticity coefficient to the analysis of various phenomena in the architecture of cities, works of art and social life is demonstrated. The informational measure of order, harmony and chaos in nature is analyzed.

I. The quality of information available about the system can be quantified based on the Shannon formula for informational entropy, as well as expressions for information redundancy and the coefficient of stochasticity.

Ii. There are different views on the concept of information and its values. The ratio of harmony and chaos in the system is amenable to quantitative analysis and can be investigated for optimality.

The measure of information on Shannon

In section 2.4, the famous Boltzmann formula was given, which determines the relationship of entropy with the statistical weight P of the system

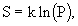(one)

In the middle of the 20th century (1948), a theory of information was created, with the advent of which the function introduced by Boltzmann (1) experienced a rebirth. American communications engineer Claude Shannon proposed to introduce a measure of the amount of information using the statistical formula of entropy.

Note that the concept of "information" is usually interpreted as "information", and the transfer of information is carried out using communication. The relationship between the amount of information and entropy was the key to solving a number of scientific problems.

Let us give a number of examples. When a coin is thrown, heads or tails fall out, this is certain information about the results of the throw. When throwing a dice, we obtain information about the loss of a certain number of points (for example, three). In which case we get more information?

The probability W of loss of the coat of arms is 1/2, the probability of loss of three points is W = 1/6. The implementation of a less probable event gives more information: the greater the uncertainty before receiving an event message (throwing a coin, dice), the greater the amount of information arrives when a message is received. Information I is related to the number of equally probable possibilities P - for a coin P = 2, for a bone P = 6. When throwing two dice, we get twice as much information as when throwing one dice: the information of independent messages is additive, and the numbers of equiprobable possibilities are multiplied. So, if there are two sets of equally probable events P ₁ and P ₂ , then the total number of events

and the amount of information I is added up, i.e.

It is known that rules (2) and (3) are subject to logarithmic functions, i.e. the dependence of the amount of information I on the number of equally probable events should be

where the constant A and the base of the logarithm can be chosen by agreement. In information theory, it was agreed to put A = 1, and the base of the logarithm to two, i.e.

When a coin is thrown, information is obtained (P = 2), which we take as a unit of information I = 1:

A bit is a binary unit of information (binary digits), it operates with two possibilities: yes or no, numbers in the binary system are written with a sequence of zeros and ones.

In general terms (conclusion), formula (4) takes the form:

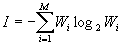. (five)

Value (5) is called Shannon informational entropy.

Such an approach to the quantitative expression of information is far from universal, since the accepted units do not take into account such important properties of information as its value and meaning. Abstraction from specific properties of information (meaning, its value) about real objects, as it turned out later, allowed us to identify the general patterns of information. The units (bits) proposed by Shannon for measuring the amount of information are suitable for evaluating any messages (birth of a son, results of a sports match, etc.). In the future, attempts were made to find such measures of the amount of information that would take into account its value and meaning. However, universality was lost immediately: for different processes, criteria of value and meaning are different. In addition, the definitions of the meaning and value of information are subjective, and the measure of information proposed by Shannon is objective. For example, the smell carries a huge amount of information for the animal, but is elusive for humans. The human ear does not perceive ultrasonic signals, but they carry a lot of information for a dolphin, etc. Therefore, the measure of information proposed by Shannon is suitable for studying all types of information processes, regardless of the consumer’s tastes.