6.2 Shannon Formula

In section 2.4, the famous Boltzmann formula was given, which determines the relationship of entropy with the statistical weight P of the system

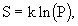
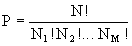(one)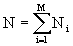

.

The probability W _i occurrence of the state i is equal to

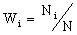, i = 1,2, ..., M, and .

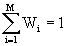As already noted, in the middle of the 20th century (1948) an information theory was created, with the advent of which the function introduced by Boltzmann (1) experienced a rebirth. American communications engineer Claude Shannon proposed to introduce a measure of the amount of information I using the statistical formula of entropy and take I = 1 as a unit of information:

Such information is obtained by throwing a coin (P = 2).

A bit is a binary unit of information (binary digits), it operates with two possibilities: yes or no, numbers in the binary system are written with a sequence of zeros and ones.

Using formulas (1) and (2), we calculate the information contained in a single message. It consists of N letters of a language consisting of M letters.

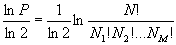I = log ₂ P = (3)

We transform the last dependence using the approximate Stirling formula

We present in the formula (3) the parameters N! and N _i ! in the form (4), we get

I = .

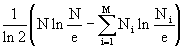Express N _i through W _i N, then the last expression takes the form

I = = = .

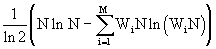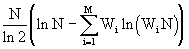Let's go to logarithm with base two.

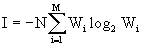. (five)

The last formula allows you to quantify the information I, which is in the message of the N letters of the language containing M letters, and one letter has the information I ₁ = I / N, i.e.

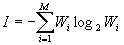. (6)

The quantity (6) is called Shannon entropy.

Recall that the expression (1) for thermodynamic entropy after similar transformations can be represented in the form (5)

.

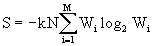More information about the relationship of thermodynamic and informational entropy