Lecture
As mentioned earlier, photons are generated in the laser during stimulated emission: exciting atoms, we create population inversion and when the atom returns to its normal state, light of a single phase and frequency is emitted, that is, coherent radiation occurs. If active atoms are pumped (excited) by external sources weakly, the laser acts like a normal lamp. Atoms independently of each other emit wave trains with random phases and are considered as oscillating dipoles, oscillating randomly. If you increase the pumping, then suddenly, with a very small change in pumping, the laser goes into a new, highly organized state. Atomic dipoles are now oscillating in phase, although they are excited by pumping randomly. Thus, self-organization manifests itself in the atomic system. The high coherence of laser radiation is caused by the cooperative behavior of atomic dipoles, i.e. Interaction.
The rate of photon production, or the change in the number of photons dn / d with time 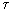 =
= 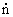 determined by the equation of the form
determined by the equation of the form
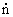 = Gain - Losses (1)
= Gain - Losses (1) The increment is caused by stimulated emission and is proportional to the number of already existing photons n and the number of excited N atoms, i.e.
Losses due to the escape of photons through the ends of the laser. Suppose that the escape rate is proportional to the number of photons available, i.e.
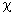 n, 2
n, 2 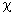 = 1 /
= 1 / 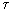 0 , (3)
0 , (3) 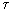 0 is the photon lifetime in the laser.
0 is the photon lifetime in the laser. The number of excited N atoms decreases due to the emission of photons, that is, N (n), and Eq. (1) becomes nonlinear. If, in the absence of lasing, the number of excited atoms is maintained by external pumping at a constant level N 0 , then due to the generation, the true number of excited atoms will be smaller by 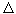 N. This is a decrease
N. This is a decrease 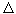 N is proportional to the number of photons in the laser n, since these photons constantly force the atoms to return to the ground state; in this way
N is proportional to the number of photons in the laser n, since these photons constantly force the atoms to return to the ground state; in this way
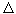 N,
N, 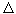 N =
N = 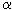 n. (four)
n. (four) Substituting (1) and (2) into (4), we obtain the basic equation of a simplified laser model
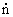 = -kn-k 1 n 2 , k = 2
= -kn-k 1 n 2 , k = 2 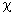 - GN 0 (5)
- GN 0 (5) If the number of excited atoms N 0 is small, then k is positive, and for large N 0 the coefficient k may become negative; sign change occurs when
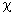 (6)
(6) This is the lasing threshold condition. It is known that for k> 0 there is no lasing, and for k <0 lasing occurs.
The solution of the differential equation (5) is
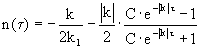 , (7)
, (7) 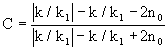 .
. Here n 0 = n (0) is the initial state.
The temporal behavior of function (7) is such that it approaches the steady state n = 0 or n = | k / k 1 | regardless of the initial value n 0 , but depending on the signs of k, k 1 .
In a two-mode laser, photons of two types 1 and 2 are generated in the amount of n 1 and n 2 . By analogy with (5), (6), the velocity equations have the form
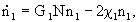 |  |
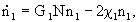 |
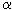 1 n 1 -
1 n 1 - 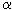 2 n 2
2 n 2 Condition of stationarity
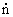 1 =
1 = 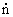 2
2 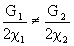
Comments
To leave a comment
Synergetics
Terms: Synergetics