6.4 Evaluation of information in the text

It is supposed to do the following experience. On 32 cards write all the letters of the Russian alphabet. After thoroughly mixing the cards, they are retrieved at random, write a letter, return the card to the box, mix again, remove the card, write the letter, etc. Having done this procedure 30-40 times, we get a set of letters. The mathematician R. Dobrushin as a result of this experiment received a set of letters given in the first line of the table. one.

Table 1

The alternation of letters is random, chaotic. The entropy of the text is great. According to the proposed method, the probability of extracting any of the letters is the same, i.e.

The probability of extracting a blank card (the gap between words) is also equal to 1/32: one space falls on 32 letters.

The entropy of the appearance of each next letter in the text is calculated by Shannon's formula

.

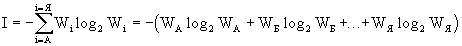If the probabilities of the appearance of letters are the same, W _А = W _Б = ... = W _Я , then we get the entropy I ~ 5 bits.

In real texts, the frequency of occurrence of each letter and the intervals are different. In tab. 2 shows the frequency of W _i letters in Russian. Because of the different likelihood of the appearance of different letters in real texts, their entropy is less than in the first experiment. In the second experiment, not 32 cards are placed in the box anymore, but more: the number of cards is proportional to the probabilities of letters. For example, on 1 card with the letter F (W _F = 0.002) there are 45 cards with the letter O (W _O = 0.090). Then, as in the first experiment, the cards are pulled out and returned. As a result, phrase 2 (Table 1) appears, which is more ordered.

table 2

First of all, the absurdly long words disappeared from the text.

Secondly, in phrase 2, vowels and consonants alternate more evenly, but, nevertheless, not everything can even be read, not to mention the meaning.

Substitute in the formula of Shannon the probability of occurrence of individual letters

The amount of information in a message per one letter has decreased from 5 to 4.35 bits, because we have information about the frequencies of occurrence of letters.

But in the language there is a frequency dictionary, where not only the frequencies of individual letters, but also their combinations (paired, triple, etc.) are taken into account. If we take into account the probability of 4 letter combinations in the Russian text, we get the phrase 3 (Table 1).

As more and more lengthy correlations are taken into account, the similarity of the “texts” obtained with the Russian language increases, but the meaning is still far away.