Lecture
Apply the laws of thermodynamics of open systems to living organisms. For this, a living organism (open system), together with its environment, is separated from the rest of the world by an adiabatic shell. Then it is possible to apply the laws of thermodynamics to such a system.
Consider three examples from this area -
cosmonaut in the cabin of the spacecraft,
living cell division and
man in the steam room.
Example 1. An astronaut in a spacecraft.
The interior of the cabin is isolated from the surrounding space. The astronaut is an open system, the change in its entropy dS (k) is
dS (k) = d i S (k) + d e S,
where d i S (k) is the production of entropy by the astronaut, d e S is the entropy flow due to the exchange of heat and substance of the cosmonaut with the environment.
The entropy change dS (c) of the medium around the astronaut is
dS (s) = - d e S,
and total entropy changedS = dS (k) + dS (s) = d i S (k) > 0,
since the entropy dS of an isolated system increases by the astronaut’s entropy production d i S (k) .If the astronaut is young and healthy, his condition is stationary and his entropy does not change, i.e.
dS (k) = d i S (k) + d e S = 0.
In the stationary state, the entropy production inside the system d i S (k) > 0, is compensated by its outflow to the outside d e S <0.
It can be specifically shown that the outflow of d e S entropy is higher than the entropy of substances consumed in food; the amount of energy in the steady state does not change.
The famous physicist Schrödinger in 1949 raised the following question: “what then is that precious SOMETHING contained in our food that protects us from death?” A living organism increases the entropy S  S max and brings him to death. It is possible to escape from this state if there is a large entropy outflow to the medium or, to put it differently, because of the extraction of negative entropy from the medium; the latter is called "negentropy". Negative entropy is that precious SOMETHING that the body eats. In metabolism, the release of the body from its entropy is essential.
S max and brings him to death. It is possible to escape from this state if there is a large entropy outflow to the medium or, to put it differently, because of the extraction of negative entropy from the medium; the latter is called "negentropy". Negative entropy is that precious SOMETHING that the body eats. In metabolism, the release of the body from its entropy is essential.
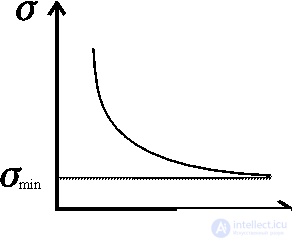
Figure 1. The dependence of the dissipation function on time.
Prigogine showed that if a stationary state of an open system is close to an equilibrium state, then the dissipation function has a minimum, that is, as it approaches a stationary state, it decreases d 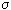 / d
/ d 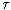 <0, and in steady state d
<0, and in steady state d 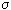 / d
/ d 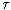 = 0 (fig. 3.3). In other words, the growth of a young organism (powerful metabolism, increased metabolism) in the terms given will be recorded
= 0 (fig. 3.3). In other words, the growth of a young organism (powerful metabolism, increased metabolism) in the terms given will be recorded
dS (k) = d i S (k) + d e S <0,
and aging, on the contrary, is accompanied by an increase in entropy, there is no compensation for it due to outflow to the outsidedS (k) = d i S (k) + d e S> 0,
and death occurs when S = S max .Example 2 Cell division.
The cell is an open system and its entropy balance is expressed by the ratio
dS = d i S + d e S.
Imagine a cell in the form of a ball of radius r, the entropy production d i S is proportional to the volume 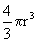 and the outflow d e S is proportional to the surface area 4
and the outflow d e S is proportional to the surface area 4 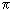 r 2 . Therefore, the change in entropy dS is
r 2 . Therefore, the change in entropy dS is
dS = A 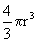 - AT 4
- AT 4 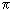 r 2 ,
r 2 ,
It is easy to see that at r = 3B / A, dS = 0. At smaller r <3B / A, the entropy outflow is higher than its production. When r> 3B / A, dS> 0 and substances with excessive entropy accumulate in the cell and the cell overheats. Therefore, when r = 3B / A, the cell must divide, otherwise it will die, and in the new two cells the volume will not change, and the surface will increase. The radii r 1 of new cells are easy to find.
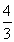 = 2
= 2 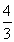
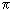 r 1 3 , r 3 = 2r 1 3 , r 1 = r /
r 1 3 , r 3 = 2r 1 3 , r 1 = r / 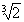 .
.
The change in entropy in two new cells is dS = 2 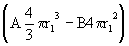 . When r = 3V / A = r 1
. When r = 3V / A = r 1 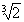 or r 1 =
or r 1 = 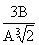 we get dS = 36
we get dS = 36 
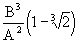 <0, i.e. the entropy outflow increased in
<0, i.e. the entropy outflow increased in 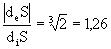 time.
time.
So, cell division is associated with entropy outflow, these are non-equilibrium processes, and crystal growth occurs when the free energies and the melt are equal; here an equilibrium phase transition takes place.
Example 3. Man in the bath
Consider the behavior of the human body when it is in the steam room.
We define the production of entropy d i S of a person in any conditions. It should be noted that it was established experimentally on the basis of direct calometry (change in a person’s losses in the calorimeter), as well as using indirect calometry (based on gas exchange during human breathing), that a person produces 100 watts of power in comfort. By the way, the data of direct and indirect calometry with a long experience are the same on average. We will assume that a person stays in the steam room for 2 hours or 7,200 seconds, during which time he “develops” energy Q = 100W * 7200s = 7.2 * 10 5 J, we take a person's body temperature of 36 ° C or about 300 ° K, i.e. entropy production equals
d i S = 7.2 * 10 5/3 * 10 2 = 2.4 * 10 3 J / K.
Suppose that in the process of soaring a person lost in weight a mass of m = 2 kg, i.e., he evaporated 2 kg of water in 2 hours. Heat of evaporation of water (H = 4 * 10 4 J / mol), molecular weight of water - M (H 2 0) = 18 g / mol, energy loss dQ = m * H * M = 2 * 4 * 10 4 * 18 = 12.8 * 10 5 j.
Find the entropy flux d e S = dQ / T = 12.8 * 10 5/3 * 10 2 = 4.2 * 10 3 J / K.
Let us compare the entropy production d i S and the entropy outflow d e S
d i S = 2.4 * 10 3 JK., d e S = 4.2 * 10 3 J / K.
In this case, we are dealing with an entropy pump, under the action of which there is an outflow of entropy from the system, which should lead individual human organs to a more organized state and, if this process is carried out within moderate limits, then the general condition of the person after the bath should improve.
Comments
To leave a comment
Synergetics
Terms: Synergetics