4.2 Entropy pump. Dissipative structures

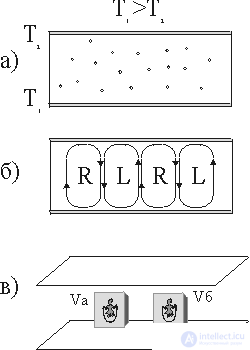Fig. 1 Transfer of heat flow in gas:
a) molecular transfer;
b) convective currents rotating clockwise (R) and counterclockwise (L) arrows;
c) the observer in volumes V _a and V _b .

In 1901, physicist Benard discovered a strange effect in the convective motion of gas and liquid. Consider a layer of liquid heated from below (Fig. 1, a) for small values ​​of the product of Grashof numbers Gr and Prandtl Pr (Gr * Pr <10 ³ ). (Read more about Gr and Pr.) Heat is transferred as a result of the process of thermal conductivity, i.e. due to the molecular transfer of energy of randomly moving gas or liquid molecules.

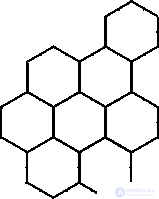
The Benard effect can also be observed in the following experiment: vegetable or silicone oil is placed in a shallow vessel and heated evenly from the bottom. There is a temperature difference between the upper and lower surfaces. With T> T _cr arises convection and the liquid is divided into hexagonal cells (Fig. 2), i.e. a dynamic, organized, ordered structure arises - this is one type of dissipative structure.

Let us look at the phenomena of chaos and order from the position of a miniature observer placed in volumes V _A and V _{B of a} fluid (Fig. 1, c) under conditions of chaotic fluid movement between the plates (Fig. 1, a).

The observer builds his judgments only on observations of the environment, he can not determine which of the two volumes (V _A or V _B ) he is. In other words, all the volumes that can be distinguished in a liquid will be indistinguishable between themselves and the observer no matter where they put it - everything is the same everywhere, and it does not have the inner capacity to perceive space. If such a system is disturbed, for example, to change its temperature somewhere, then it decays in time. This is a steady state. In this state, the observer is not able to have his own ideas about either time or space. The situation changes significantly if the convection currents shown in fig. 1, b. For example, an observer can decide where he is by observing the nature of rotation (clockwise R or counterclockwise L) in his cell. By counting the number of cells that he passes, he can get an idea of ​​space: he discovers the orderliness of the system. In other words, there are correlations between remote parts of the system, i.e., we observe the effect of self-organization. We draw attention to the difference between the long-range nature (of the order of cm and more) of these correlations and the short-range nature of the intermolecular forces (of the order of angstroms 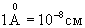). Such a strong difference in scales expresses a deep difference between equilibrium and non-equilibrium states. What is the mechanism of the "coordinated action" of molecules at distances hundreds of millions of times longer than the distances of intermolecular interactions?

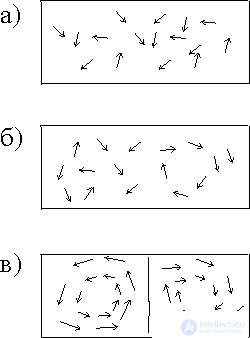Figure 3. The origin of convective motion:
a) chaotic motion;
b) convective cells arise and collapse
c) Benard cells .

In 1988, Benard vortexes were numerically simulated: 5050 hard disks were investigated, moving and colliding in a two-dimensional box. The upper and lower bounds of the box were maintained at different temperatures (the disks, colliding with each side, flew off at a new speed corresponding to the wall temperature). Further, the disks were subjected to the action of an external force simulating the force of gravity (it is directed against gradT). Initial position: the disks are randomly distributed in a box, as in the equilibrium state of a particle at a certain temperature T (Fig. 3, a). If a 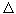T < T _cr ( 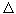T _cr is associated with the criterion K _cr ), then the formation of small vortices in the system is observed, which soon disappear (Fig. 3, b). With 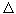T 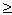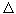T _cr and higher vortices do not disappear. They involve in their movement an increasing number of "molecules" until the entire liquid layer is involved in the vortex motion (Fig. 3, c). Note that this experiment is characterized by high reproducibility: under the same conditions, the excess T _cr always leads to a convection pattern. However, it is possible to change the direction of rotation in the cells. For example, in the left cell (Fig. 1, b), the right rotation (R) can be replaced by the left (L). So, as soon as you exceed the value 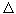T _kr , convection currents (determinism) will definitely appear, but the direction of their rotation is unpredictable (randomness). Amazing collaboration between contingency and certainty. The above considerations are presented in fig. 4: we see that far from equilibrium, the system can adapt to the environment in several different ways, and only the case decides which of these solutions will be implemented [3, 6].

You can make the statement that when T = 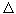T _cr appears instability process: near equilibrium, the second law still ensures that the fluctuations fade out and eventually die out. Equilibrium systems are controlled by the experimenter. In nonequilibrium systems, the experimenter cannot control the spontaneous occurrence of vortices. Uncontrolled fluctuations can increase and play a crucial role.

So, instability means that fluctuations can stop being just "noise" and turn into a factor directing the global evolution of the system. The same event, the same fluctuation, can be completely negligible if the system is stable and become very significant for a nonequilibrium system.

One more important feature should be noted: in fig. 3 presents the results of time averaging for a large number of collisions (more than a million). If one were to take a snapshot (fig. 3, b), then the disorder of the system could be seen, that is, one would not pay attention to the appearance of ordered vortices. A demon observing the instantaneous state of pictures 3, a and 3, b would not be able to notice the elements of order in fig. 3, b. In either case, he would see the intricate movement of molecules.

What happens when the first structuring threshold is exceeded 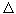T = 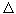T _cr1 and the temperature difference will increase further? In some area 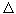T> 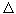T _cr1 Benar cells will exist, however, some of their characteristics will begin to change. Then, after going through the second critical state 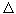T 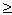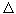T _cr2 the flow structure will become blurred and a new regime will _appear , characterized by a disordered dependence of variables over time - this is the so-called turbulent mode.

Above was considered one of the many examples when a set of particles is transformed into a system, and it has new properties of cooperative interaction that are not limited to the properties of its constituent elements.

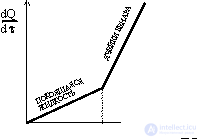
We present an attempt to quantitatively describe the observed effects. In fig. 5 shows the dependence of the heat flux dQ / d 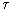= q J / s, W from the temperature difference 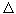T on the plates. With 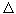T = 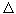T _cr occurs a sharp break in the dependence dQ / d and structure formation occurs. Since the system in question exchanges heat with the environment, it is possible to imagine the total flow of entropy through the surface of a liquid using the formula (dissipation function)

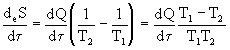<0

Fluid under these conditions exports entropy. Under stationary conditions, this entropy outflow is compensated by entropy production (internal friction, thermal conductivity). As noted above, such systems are called dissipative: open, far from equilibrium, structure-forming, self-organizing systems.

Dissipative systems make it necessary to take a fresh look at the problem of the connection between the second law of thermodynamics and the laws of classical mechanics. Machine imitation of the dynamics of colliding particles in order to follow the evolution of the evolution of such a system was implemented by S. I. Yakovenko. He considered a closed system with many particles, set the laws of interaction of particles from classical mechanics, other effects on the fate of the system were excluded. Since the maximum of entropy corresponds to the state of maximum chaos, then according to the nature of the motion of the particles, one can also imagine the second law in the system of particles. A large number of computer experiments were performed, which led the author to the following conclusion: the state of maximum chaos is not realized by itself, as a consequence of the evolution of particles according to the laws of classical mechanics [3].

Further, S.I. Yakovenko discovered that it is enough to introduce some kind of stochastic principle in one way or another in order to obtain the picture observed in nature. In other words, a connection is possible between the statistical principle inherent in the microworld and the property of the system characterized by the magnitude of entropy. And the latter belongs to the macro world, that is, the system has properties that are not derived from the properties of the elements.

It is possible to take a fresh look at the second law of thermodynamics, as a system law: it makes sense for a large number of particles and therefore we do not deduce from the laws of mechanics and the laws of pair interactions. An aggregate of particles may have properties that are absent from its individual elements. System features seem to appear at a certain level of system complexity when the latter loses stability and the motion of particles becomes chaotic. The reason for the destruction of the order here is randomness.

Many examples can be cited when a set of particles is transformed into a system and new properties of cooperative interaction arise in it. We will return to this issue in the section on social phenomena (go to).

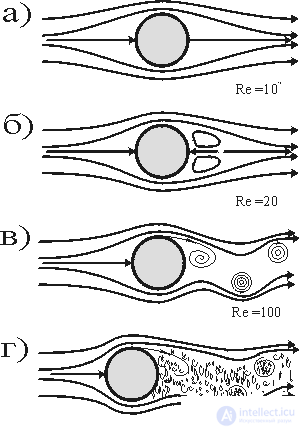
Fig. 6. The birth of turbulence when a ball flows around a fluid:
a) laminar flow (Re = 10 ^-2 );
b) the appearance of vortices in the aft part (Re = 20);
c) the development of vortices (Re = 10 ² );
d) developed turbulence (Re> 10 ⁴ ).

Consider a cylinder whose axis is perpendicular to the velocity V of a moving fluid. In fig. 6, a) shows schematically the flow lines of a fluid at a low speed of its movement. The nature of these lines depends not only on speed, but also on kinematic viscosity. 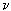= 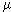/ 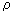( 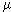- fluid viscosity 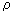- its density) and the diameter d of the cylinder. These numbers are combined in a dimensionless Reynolds complex, Re = Vd / 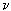which is more complete than one speed describes the pattern of fluid flow around a cylinder. So, for small numbers Re 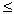20 current lines are stationary, i.e. they do not change with time. But after the speed exceeds a certain threshold, recirculation vortices appear in the wake of the cylinder (Fig. 6, b). The stationary mode disappears, giving way to a chain of vortices, rotating alternately in one, then in the other direction. This phenomenon is called the Bener-Karman vortex path. In fig. 6 depicts the evolution of vortices for different values. 20 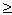Re 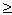10 ⁶ . When Re> 20, a pair of vortices appears, with Re> 10 ^{2, the} vortices oscillate. At even higher speeds (Re> 10 ⁶ ), an irregular picture appears - a turbulent flow. In the latter one can also see the emergence of a new picture of self-organization — order in chaos.

We emphasize the universal nature of the periodic phenomena described here: the Benar-Karman trail can be found in the structure of clouds created by the wind over the city and behind the Big Red Spot on Jupiter.