Lecture
Consider the so-called. Cantor set and Sierpinski carpet. These sets have geometric invariance and are known as "sets of middle thirds". The segment of unit length [0, 1] is divided into three equal parts, and the middle of them, the interval (1/3, 2/3), is cut out. With each of the other segments do the same (Fig. 1).
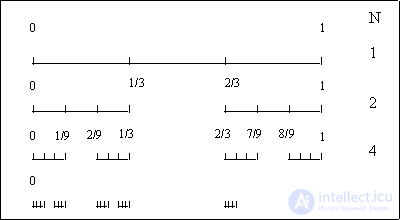
We get a sequence of segments all decreasing in length. At the first stage we have one segment, at the second - two, at the third - four, on the kth - 2 k segments, 3 k in length. With k 
 we obtain a set of points, which is called a Cantor set. The total length of all cut segments is equal to one.
we obtain a set of points, which is called a Cantor set. The total length of all cut segments is equal to one.
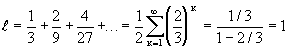 .
. The generalization of the Cantor set of middle thirds to the case of flat figures leads to the Serpinsky carpet.
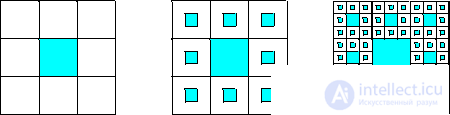
Take a square with a side equal to one, and divide it into nine equal squares; during the first iteration (k = 1) we delete the central square; we will do the same with each of the remaining eight squares (k = 2), etc. (Fig. 2). Intersection obtained at k 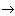
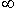 The sets are the Sierpinski carpet. Cantor set, roughly speaking, is like "everywhere full of holes."
The sets are the Sierpinski carpet. Cantor set, roughly speaking, is like "everywhere full of holes."
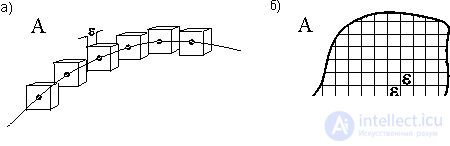
There is an important quantitative characteristic of the Cantor set - the fractional dimension. Consider some set A and try to completely cover it with segments, squares or hypercubes with a side  (Fig. 3). Let N be the minimum number of cubes or squares needed to cover A. Consider the limit
(Fig. 3). Let N be the minimum number of cubes or squares needed to cover A. Consider the limit
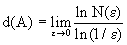 . (one)
. (one) The value d (A) = dF is a metric dimension and is called the fractal dimension.
 :
: Find the fractal dimension of a square with side 1. In order to close this square you must have (1 /  ) 2 squares with a side
) 2 squares with a side 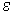 . Therefore, d is equal to
. Therefore, d is equal to
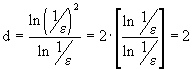 ,
, Find d for the Cantor set (Fig. 1). At the first splitting, it is necessary to have two segments 1/3 length to cover; for the second partitioning, four segments of length 1/9 are required, and generally, for the nth partitioning, it is necessary to have 2 n segments of length (1/3) n . So, the Cantor set consists of N = 2 n divided intervals of length (1/3) n each. Using the definition (1), we get
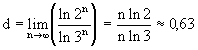 .
. Thus, the Cantor set is intermediate between a point (d = 0) and a line (d = 1), that is, it is a fractal.
Let us determine the fractal dimension of the Sierpinski carpet. We have at the first (k = 1) and subsequent partitions
| k = 1 | N = 8 = 8 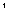 | 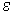 = (1/3) = (1/3) 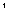 |
| k = 2 | N = 8 * 8 = 8  | 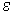 = (1/3) = (1/3)  |
| k = 3 | N = 8 * 8 * 8 = 8 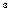 | 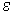 = (1/3) = (1/3) 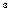 |
| k = n | N = 8 n | 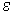 = (1/3) n = (1/3) n |
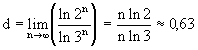
Consequently, the Sierpinski carpet is no longer a line with dimension 1, but also not a surface, the dimension of which is 2. It is something between the line and the surface. The most unexpected is the fact that in nature there are objects that represent an analogue of the Sierpinski carpet with dimension 1 <d <2. These are fractal aggregates of colloidal particles.
Consider now another classic fractal object - a snowflake. The snowflake has an infinite perimeter, although it bounds the end region of the plane. Take an equilateral triangle, divide each of its sides into three parts, and for each of the three central thirds we construct an equilateral triangle of smaller dimensions. Iterating this construction infinitely many times, we obtain a fractal object, sometimes called a Koch curve, whose dimension is d = ln4 / ln3 ~ 1.26 (Fig. 4).

In a similar way you can build a lot of different fractals. We give some of them.




Comments
To leave a comment
Synergetics
Terms: Synergetics