Lecture
In systems within which physical, chemical, and biological processes take place, entropy is always produced. This production occurs at a certain rate.
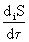 , (one)
, (one)
Entropy production per time unit d i S / d 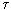 in unit volume V of an open system, we denote by the letter
in unit volume V of an open system, we denote by the letter 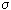 by this definition
by this definition
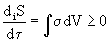 . (2)
. (2)
Magnitude 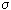 called the dissipation function * .
called the dissipation function * .
Let us pay attention to the second principal feature introduced into the reasoning — time has appeared, since the rate of entropy production is determined. Recall that the first fundamental feature consisted in the possibility of a decrease in the entropy dS <0 in an open system. So, the transition from thermostatics, which was classical thermodynamics to time-varying processes, i.e. to dynamics, to kinetics. Thermostatics considers equilibrium processes, i.e. proceeding very slowly, where at each stage equilibrium is reached. Above in formulas (1) and (2), the transition to nonequilibrium processes is complete.

Fig. 1. Heat fluxes: a.- from the first body to the second; b.- when melting ice in a vessel of water
The figure shows the two bodies brought into contact at different temperatures. From a hotter body to a less heated body, heat flux arises due to heat conduction, the entropy dS = dQ / T is produced. The driving force in the production of entropy is the temperature difference (T 1 -T 2 ). As will be shown below, this difference is conveniently presented in the form
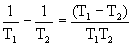 , T 1 > T 2 .
, T 1 > T 2 .
"Design" dissipation function in the form
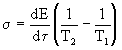 (3)
(3)
This formula reflects all elements of the entropy production process: energy flow dE / d 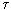 and the driving force that creates this stream. In this case, the driving force is the temperature difference. Note that E is the energy per unit volume [E] = J / m 3 .
and the driving force that creates this stream. In this case, the driving force is the temperature difference. Note that E is the energy per unit volume [E] = J / m 3 .
Consider the dimensions of the right and left sides of the formula (3). By definition, the dimension of the dissipation function [ 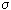 ] =
] = 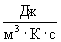 and the dimension of the right side of the formula (3)
and the dimension of the right side of the formula (3) 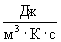 i.e. with the dimension everything is fine.
i.e. with the dimension everything is fine.
We can give the second definition of the dissipation function:
The dissipation function is equal to the product of the flow J by the force X, which causes it: 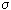 = J * X
= J * X
It is possible to construct a dissipation function not only for thermal phenomena.
For example, for electrical phenomena, the flow is the strength of the electric current I, and the force causing it is the potential difference ( 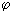 1 -
1 - 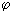 2 ) and
2 ) and 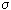
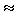 I (
I ( 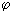 1 -
1 - 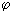 2 ). Electric current I = de / d
2 ). Electric current I = de / d 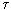 - time derivative of charge [I (
- time derivative of charge [I ( 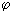 1 -
1 - 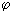 2 )] = W = J / s. For dimensional reasons, one should take the specific electric power J / cm 3 and divide it by temperature, i.e.
2 )] = W = J / s. For dimensional reasons, one should take the specific electric power J / cm 3 and divide it by temperature, i.e.
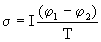 ,
,
If a chemical reaction takes place in the system, then entropy is also produced. A chemical reaction flows from more free energy to less. The role of the acting force is played by the difference of chemical potentials A, and the flow is played by the chemical reaction rate V, that is, the number of moles of a substance undergoing transformation per unit time. According to the above rules, we "construct" the dissipation function:
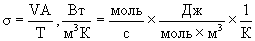
In all these cases, irreversible processes are realized. Above dissipation function 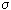 everywhere was presented as the product of the flow J by the force X, its caller.
everywhere was presented as the product of the flow J by the force X, its caller.
The reader is also advised to familiarize himself with paragraph. Interconnected processes in open systems and examples to the chapter Thermodynamics of open systems and living organisms.
In conclusion, we note that this section summarizes the works of the founders of the thermodynamics of irreversible processes L. Onzager, De Donde and I. Prigogine, who in 1977 were awarded the Nobel Prize for their work on the thermodynamics of irreversible processes and their use in chemistry and biology.
I. Prigogine (1917) - Belgian physicist, member of the Belgian Academy of Sciences, director of the International Institute of Physics and Chemistry (Belgium), member of the USSR Academy of Sciences, introduced the concepts of entropy production and entropy flow, gave a local formulation of the second beginning of TD, formulated the Prigogine theorem, the author of many monographs on nonequilibrium thermodynamics.
L. Onzager (1903 - 1976) - American chemist and physicist, professor of chemistry at several American universities. In 1931, he proved a number of theorems of thermodynamics of irreversible processes.
Comments
To leave a comment
Synergetics
Terms: Synergetics